|
Rainbow Covering
In combinatorics and computer science, covering problems are computational problems that ask whether a certain combinatorial structure 'covers' another, or how large the structure has to be to do that. Covering problems are Optimization (mathematics), minimization problems and usually integer linear programs, whose dual problems are called packing problems. The most prominent examples of covering problems are the set cover problem, which is equivalent to the Hitting set, hitting set problem, and its special cases, the vertex cover problem and the edge cover problem. Covering problems allow the covering primitives to overlap; the process of covering something with non-overlapping primitives is called decomposition (other), decomposition. General linear programming formulation In the context of linear programming, one can think of any minimization linear program as a covering problem if the coefficients in the constraint matrix (mathematics), matrix, the objective function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science. Combinatorics is well known for the breadth of the problems it tackles. Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving an ''ad hoc'' solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Arboricity
The arboricity of an undirected graph is the minimum number of forests into which its edges can be partitioned. Equivalently it is the minimum number of spanning forests needed to cover all the edges of the graph. The Nash-Williams theorem provides necessary and sufficient conditions for when a graph is ''k''-arboric. Example The figure shows the complete bipartite graph ''K''4,4, with the colors indicating a partition of its edges into three forests. ''K''4,4 cannot be partitioned into fewer forests, because any forest on its eight vertices has at most seven edges, while the overall graph has sixteen edges, more than double the number of edges in a single forest. Therefore, the arboricity of ''K''4,4 is three. Arboricity as a measure of density The arboricity of a graph is a measure of how dense the graph is: graphs with many edges have high arboricity, and graphs with high arboricity must have a dense subgraph. In more detail, as any n-vertex forest has at most n − 1 edges ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Proof
A mathematical proof is a deductive reasoning, deductive Argument-deduction-proof distinctions, argument for a Proposition, mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning that establish logical certainty, to be distinguished from empirical evidence, empirical arguments or non-exhaustive inductive reasoning that establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in ''all'' possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Independent Set (graph Theory)
In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set S of vertices such that for every two vertices in S, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in S. A set is independent if and only if it is a clique in the graph's complement. The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening. A maximal independent set is an independent set that is not a proper subset of any other independent set. A maximum independent set is an independent set of largest possible size for a given graph G. This size is called the independence number of ''G'' and is usually denoted by \alpha(G). The optimization problem of finding such a set is called the maximum independent set problem. It is a strongly NP-hard problem. As ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear SAT
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) asks whether there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the formula's variables can be consistently replaced by the values TRUE or FALSE to make the formula evaluate to TRUE. If this is the case, the formula is called ''satisfiable'', else ''unsatisfiable''. For example, the formula "''a'' AND NOT ''b''" is satisfiable because one can find the values ''a'' = TRUE and ''b'' = FALSE, which make (''a'' AND NOT ''b'') = TRUE. In contrast, "''a'' AND NOT ''a''" is unsatisfiable. SAT is the first problem that was proven to be NP-complete—this is the Cook–Levin theorem. This means that all problems in the complexity class NP, which includes a wide range of natural decision and optimization problems, are at most as difficult to solve as SAT. There is no know ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
NP-hardness
In computational complexity theory, a computational problem ''H'' is called NP-hard if, for every problem ''L'' which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from ''L'' to ''H''. That is, assuming a solution for ''H'' takes 1 unit time, ''H''s solution can be used to solve ''L'' in polynomial time. As a consequence, finding a polynomial time algorithm to solve a single NP-hard problem would give polynomial time algorithms for all the problems in the complexity class NP. As it is suspected, but unproven, that P≠NP, it is unlikely that any polynomial-time algorithms for NP-hard problems exist. A simple example of an NP-hard problem is the subset sum problem. Informally, if ''H'' is NP-hard, then it is at least as difficult to solve as the problems in NP. However, the opposite direction is not true: some problems are undecidable, and therefore even more difficult to solve than all problems in NP, but they are probably not NP- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Subset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. When quantified, A \subseteq B is represented as \forall x \left(x \in A \Rightarrow x \in B\right). One can prove the statement A \subseteq B by applying a proof technique known as the element argument:Let sets ''A'' and ''B'' be given. To prove that A \subseteq B, # suppose that ''a'' is a particular but arbitrarily chosen element of A # show that ''a'' is an element of ''B''. The validity of this technique ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Real Line
A number line is a graphical representation of a straight line that serves as spatial representation of numbers, usually graduated like a ruler with a particular origin (geometry), origin point representing the number zero and evenly spaced marks in either direction representing integers, imagined to extend infinitely. The association between numbers and point (geometry), points on the line links elementary arithmetic, arithmetical operations on numbers to geometry, geometric relations between points, and provides a conceptual framework for learning mathematics. In elementary mathematics, the number line is initially used to teach addition and subtraction of integers, especially involving negative numbers. As students progress, more kinds of numbers can be placed on the line, including fractions, decimal fractions, square roots, and transcendental numbers such as the pi, circle constant : Every point of the number line corresponds to a unique real number, and every real number to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Interval (mathematics)
In mathematics, a real interval is the set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a bound. A real interval can contain neither endpoint, either endpoint, or both endpoints, excluding any endpoint which is infinite. For example, the set of real numbers consisting of , , and all numbers in between is an interval, denoted and called the unit interval; the set of all positive real numbers is an interval, denoted ; the set of all real numbers is an interval, denoted ; and any single real number is an interval, denoted . Intervals are ubiquitous in mathematical analysis. For example, they occur implicitly in the epsilon-delta definition of continuity; the intermediate value theorem asserts that the image of an interval by a continuous function is an interval; integrals of real functions are defined over an interval; etc. Interval ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
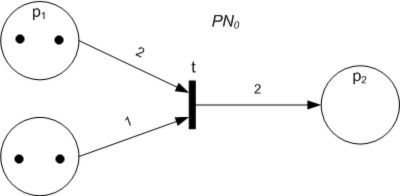
Petri Net
A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements: places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Pet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |