|
Repeated Game
In game theory, a repeated game (or iterated game) is an extensive form game that consists of a number of repetitions of some base game (called a stage game). The stage game is usually one of the well-studied 2-person games. Repeated games capture the idea that a player will have to take into account the impact of their current action on the future actions of other players; this impact is sometimes called their reputation. Single stage game or single shot game are names for non-repeated games. Example Consider two gas stations that are adjacent to one another. They compete by publicly posting pricing, and have the same and constant marginal cost ''c'' (the wholesale price of gasoline). Assume that when they both charge , their joint profit is maximized, resulting in a high profit for everyone. Despite the fact that this is the best outcome for them, they are motivated to deviate. By modestly lowering the price, either can steal all of their competitors' customers, nearly doub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed two-person zero-sum games, in which a participant's gains or losses are exactly balanced by the losses and gains of the other participant. In the 1950s, it was extended to the study of non zero-sum games, and was eventually applied to a wide range of Human behavior, behavioral relations. It is now an umbrella term for the science of rational Decision-making, decision making in humans, animals, and computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimax
Minimax (sometimes Minmax, MM or saddle point) is a decision rule used in artificial intelligence, decision theory, combinatorial game theory, statistics, and philosophy for ''minimizing'' the possible loss function, loss for a Worst-case scenario, worst case (''max''imum loss) scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty. Game theory In general games The maximin value is the highest value that the player can be sure to get without knowing the actions of the other players; equivalently, it is the lowest value the other players can force the player to receive when they know the player's action. Its formal definition is: :\underline = \max_ \min_ W ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Aumann
Robert John Aumann (Yisrael Aumann, ; born June 8, 1930) is an Israeli-American mathematician, and a member of the United States National Academy of Sciences. He is a professor at the Center for the Study of Rationality in the Hebrew University of Jerusalem. He also holds a visiting position at Stony Brook University, and is one of the founding members of the Stony Brook Center for Game Theory. Aumann received the Nobel Memorial Prize in Economic Sciences in 2005 for his work on conflict and cooperation through game theory analysis. He shared the prize with Thomas Schelling. Early life and education Aumann was born in Frankfurt am Main, Germany, and fled to the United States with his family in 1938, two weeks before the Kristallnacht pogrom. He attended the Rabbi Jacob Joseph School, a yeshiva high school in New York City. Aumann graduated from the City College of New York in 1950 with a B.S. in mathematics. He received his M.S. in 1952, and his Ph.D. in Mathematics in 1955, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fictitious Play , in legal uses
{{Disambiguation ...
Fictitious may refer to: * Fictitious defendants * Fictitious business name * Feigned action * Ejectment, an action to recover land * John Doe, commonly named as a fictitious defendant See also * Fiction, in literary uses * Legal fiction A legal fiction is a construct used in the law where a thing is taken to be true, which is not in fact true, in order to achieve an outcome. Legal fictions can be employed by the courts or found in legislation. Legal fictions are different from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as :a_1x_1+\cdots +a_nx_n=b, linear maps such as :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrix (mathematics), matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as line (geometry), lines, plane (geometry), planes and rotation (mathematics), rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to Space of functions, function spaces. Linear algebra is also used in most sciences and fields of engineering because it allows mathematical model, modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Public Goods Game
The public goods game is a standard of experimental economics. In the basic game, subjects Information asymmetry, secretly choose how many of their Private good, private tokens to put into a public pot. The payoff of each player is her "private consumption" (her endowment minus her contribution) plus her benefit from the "public good" (the sum of contributions multiplied by a factor). The game is used to study degree of altruism and cooperation between individuals. Introduction Public goods games are fundamental in experimental economics. The nature of the experiment is incentives and the problem of free riding. Public goods games investigate the incentives of individuals who free-ride off individuals who are contributing to the common pool. A public goods game investigates behavioural economics and the actions of the players in the game. In this process, it seeks to use behavioural economics to understand the decisions of its players. It extends further to free-riding, which ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgame Perfect Nash Equilibrium
In game theory, a subgame perfect equilibrium (SPE), or subgame perfect Nash equilibrium (SPNE), is a refinement of the Nash equilibrium concept, specifically designed for dynamic games where players make sequential decisions. A strategy profile is an SPE if it represents a Nash equilibrium in every possible subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. This ensures that strategies are credible and rational throughout the entire game, eliminating non-credible threats. Every finite extensive game with complete information (all players know the complete state of the game) and perfect recall (each player remembers all their previous actions and knowledge throughout the game) has a subgame perfect equilibrium. A common method for finding SPE in finite games is backward induction, wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chainstore Paradox
The chain store paradox is a game theory problem that challenges conventional rational choice assumptions about strategic behavior in sequential games. It describes a scenario where an incumbent chain store faces sequential entry threats from multiple potential competitors in different markets. The paradox emerges from the conflict between two compelling strategies: the logically sound approach of backward induction prescribed by classical game theory, and the intuitively appealing "deterrence strategy" that involves building a reputation for aggressive behavior to discourage future market entry. While standard equilibrium analysis suggests the chain store should accommodate all entrants, real-world business behavior often follows the deterrence approach, creating an apparent contradiction between game-theoretic predictions and observed strategic decisions. This paradox has implications for behavioral economics, industrial organization, and the study of credible threats in strate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backward Induction
Backward induction is the process of determining a sequence of optimal choices by reasoning from the endpoint of a problem or situation back to its beginning using individual events or actions. Backward induction involves examining the final point in a series of decisions and identifying the optimal process or action required to arrive at that point. This process continues backward until the best action for every possible point along the sequence is determined. Backward induction was first utilized in 1875 by Arthur Cayley, who discovered the method while attempting to solve the secretary problem. In dynamic programming, a method of mathematical optimization, backward induction is used for solving the Bellman equation. In the related fields of automated planning and scheduling and automated theorem proving, the method is called backward search or backward chaining. In chess, it is called retrograde analysis. In game theory, a variant of backward induction is used to compute subgame ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgame Perfect Nash Equilibrium
In game theory, a subgame perfect equilibrium (SPE), or subgame perfect Nash equilibrium (SPNE), is a refinement of the Nash equilibrium concept, specifically designed for dynamic games where players make sequential decisions. A strategy profile is an SPE if it represents a Nash equilibrium in every possible subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. This ensures that strategies are credible and rational throughout the entire game, eliminating non-credible threats. Every finite extensive game with complete information (all players know the complete state of the game) and perfect recall (each player remembers all their previous actions and knowledge throughout the game) has a subgame perfect equilibrium. A common method for finding SPE in finite games is backward induction, wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
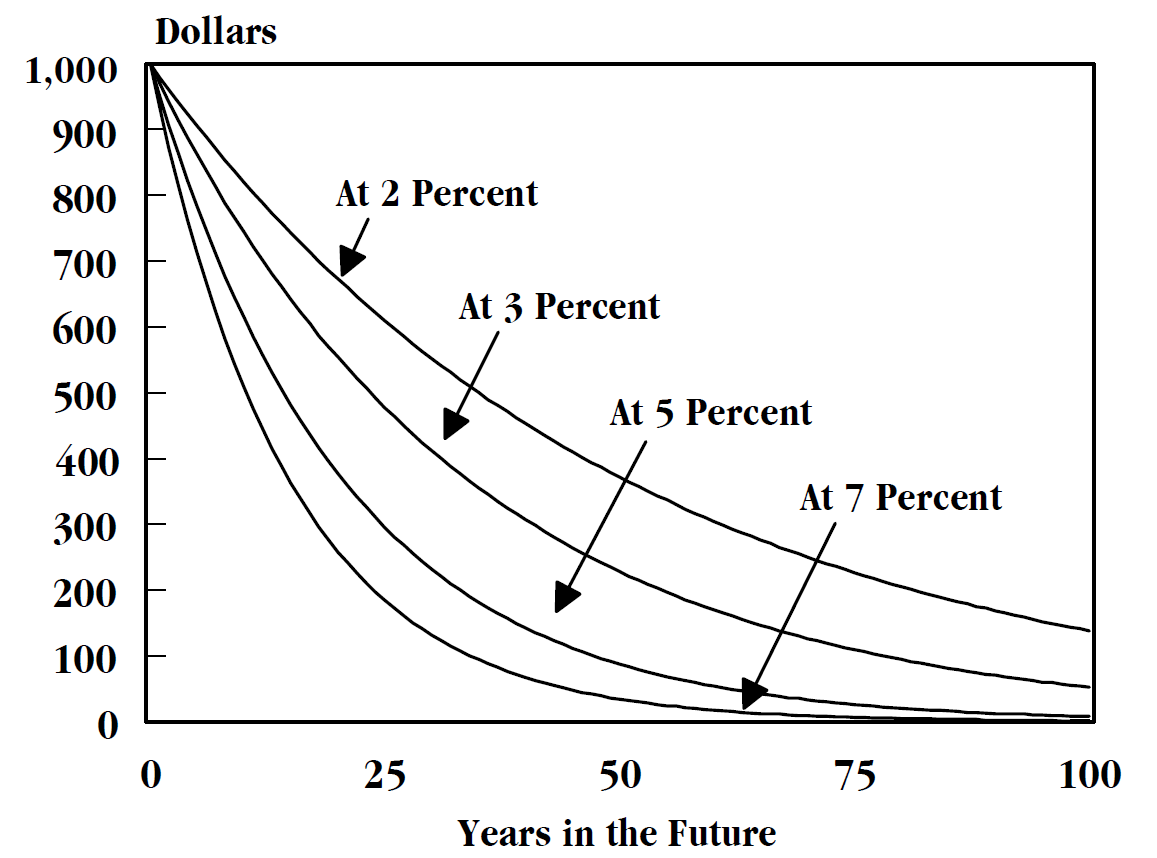
Discount Factor
In finance, discounting is a mechanism in which a debtor obtains the right to delay payments to a creditor, for a defined period of time, in exchange for a charge or fee.See "Time Value", "Discount", "Discount Yield", "Compound Interest", "Efficient Market", "Market Value" and "Opportunity Cost" in Downes, J. and Goodman, J. E. ''Dictionary of Finance and Investment Terms'', Baron's Financial Guides, 2003. Essentially, the party that owes money in the present purchases the right to delay the payment until some future date.See "Discount", "Compound Interest", "Efficient Markets Hypothesis", "Efficient Resource Allocation", "Pareto-Optimality", "Price", "Price Mechanism" and "Efficient Market" in Black, John, ''Oxford Dictionary of Economics'', Oxford University Press, 2002. This transaction is based on the fact that most people prefer current interest to delayed interest because of mortality effects, impatience effects, and salience effects. The discount, or charge, is the dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
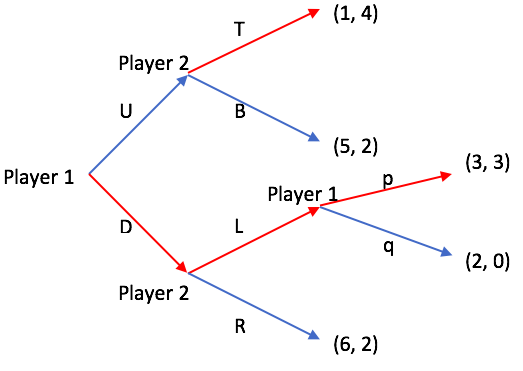
Extensive Form Game
In game theory, an extensive-form game is a specification of a game allowing for the explicit representation of a number of key aspects, like the sequencing of players' possible moves, their choices at every decision point, the (possibly imperfect) information each player has about the other player's moves when they make a decision, and their payoffs for all possible game outcomes. Extensive-form games also allow for the representation of incomplete information in the form of chance events modeled as " moves by nature". Extensive-form representations differ from normal-form in that they provide a more complete description of the game in question, whereas normal-form simply boils down the game into a payoff matrix. Finite extensive-form games Some authors, particularly in introductory textbooks, initially define the extensive-form game as being just a game tree with payoffs (no imperfect or incomplete information), and add the other elements in subsequent chapters as refinements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |