|
Remez Algorithm
The Remez algorithm or Remez exchange algorithm, published by Evgeny Yakovlevich Remez in 1934, is an iterative algorithm used to find simple approximations to functions, specifically, approximations by functions in a Chebyshev space that are the best in the uniform norm ''L''∞ sense. It is sometimes referred to as Remes algorithm or Reme algorithm. A typical example of a Chebyshev space is the subspace of Chebyshev polynomials of order ''n'' in the space of real continuous functions on an interval, ''C'' 'a'', ''b'' The polynomial of best approximation within a given subspace is defined to be the one that minimizes the maximum absolute difference between the polynomial and the function. In this case, the form of the solution is precised by the equioscillation theorem. Procedure The Remez algorithm starts with the function f to be approximated and a set X of n + 2 sample points x_1, x_2, ...,x_ in the approximation interval, usually the extrema of Chebyshev polynomial line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evgeny Yakovlevich Remez
Evgeny Yakovlevich Remez (sometimes spelled as Evgenii Yakovlevich Remez, russian: Евге́ний Я́ковлевич Ре́мез; (born 1895 in Mstislavl, now Belarus; died 1975 in Kyiv, now Ukraine) was a Soviet mathematician. He is known for his work in the constructive function theory, in particular, for the Remez algorithm and the Remez inequality. His doctoral students include Boris Korenblum Boris Isaac Korenblum (Борис Исаакович Коренблюм, 12 August 1923, Odessa, now Ukraine – 15 December 2011, Slingerlands, New York) was a Soviet-Israeli-American mathematician, specializing in mathematical analysis. Boris .... References *V K Dzyadyk, Yu A Mitropol'skii and A M Samoilenko, Evgenii Yakovlevich Remez (on the centenary of his birth) (Ukrainian), Ukrain. Mat. Zh. 48 (2) (1996), 285-286. *Yu A Mitropol'skii, V K Dzyadyk and V T Gavrilyuk, Evgenii Yakovlevich Remez (on the occasion of the ninetieth anniversary of his birth) (Russian), Ukrain. M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Approximation Theory
The ''Journal of Approximation Theory'' is "devoted to advances in pure and applied approximation theory and related areas." References External links ''Journal of Approximation Theory'' web site''Journal of Approximation Theory'' home page at Elsevier Mathematics journals Approximation theory Publications established in 1968 Elsevier academic journals English-language journals Monthly journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boost (C++ Libraries)
Boost, boosted or boosting may refer to: Science, technology and mathematics * Boost, positive manifold pressure in turbocharged engines * Boost (C++ libraries), a set of free peer-reviewed portable C++ libraries * Boost (material), a material branded and used by Adidas in the midsoles of shoes. * Boost, a loose term for turbo or supercharger * Boost converter, an electrical circuit variation of a DC to DC converter, which increases (boosts) the voltage * Boosted fission weapon, a type of nuclear bomb that uses a small amount of fusion fuel to increase the rate, and thus yield, of a fission reaction * Boosting (machine learning), a supervised learning algorithm * Intel Turbo Boost, a technology that enables a processor to run above its base operating frequency * Jump start (vehicle), to start a vehicle * Lorentz boost, a type of Lorentz transformation Arts, entertainment, and media Fictional characters * Boost (''Cars''), a character from the Pixar franchise ''Cars'' * Bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby. Note that what is meant by ''best'' and ''simpler'' will depend on the application. A closely related topic is the approximation of functions by generalized Fourier series, that is, approximations based upon summation of a series of terms based upon orthogonal polynomials. One problem of particular interest is that of approximating a function in a computer mathematical library, using operations that can be performed on the computer or calculator (e.g. addition and multiplication), such that the result is as close to the actual function as possible. This is typically done with polynomial or rational (ratio of polynomials) approximations. The objective is to make the approximation as close as possible to the actual function, typically with an accuracy close to that of the underlying computer's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floating Point
In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can be represented as a base-ten floating-point number: 12.345 = \underbrace_\text \times \underbrace_\text\!\!\!\!\!\!^ In practice, most floating-point systems use base two, though base ten ( decimal floating point) is also common. The term ''floating point'' refers to the fact that the number's radix point can "float" anywhere to the left, right, or between the significant digits of the number. This position is indicated by the exponent, so floating point can be considered a form of scientific notation. A floating-point system can be used to represent, with a fixed number of digits, numbers of very different orders of magnitude — such as the number of meters between galaxies or between protons in an atom. For this reason, floating-poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ISSN (identifier)
An International Standard Serial Number (ISSN) is an eight-digit serial number used to uniquely identify a serial publication, such as a magazine. The ISSN is especially helpful in distinguishing between serials with the same title. ISSNs are used in ordering, cataloging, interlibrary loans, and other practices in connection with serial literature. The ISSN system was first drafted as an International Organization for Standardization (ISO) international standard in 1971 and published as ISO 3297 in 1975. ISO subcommittee TC 46/SC 9 is responsible for maintaining the standard. When a serial with the same content is published in more than one media type, a different ISSN is assigned to each media type. For example, many serials are published both in print and electronic media. The ISSN system refers to these types as print ISSN (p-ISSN) and electronic ISSN (e-ISSN). Consequently, as defined in ISO 3297:2007, every serial in the ISSN system is also assigned a linking ISSN ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Doi (identifier)
A digital object identifier (DOI) is a persistent identifier or handle used to uniquely identify various objects, standardized by the International Organization for Standardization (ISO). DOIs are an implementation of the Handle System; they also fit within the URI system (Uniform Resource Identifier). They are widely used to identify academic, professional, and government information, such as journal articles, research reports, data sets, and official publications. DOIs have also been used to identify other types of information resources, such as commercial videos. A DOI aims to resolve to its target, the information object to which the DOI refers. This is achieved by binding the DOI to metadata about the object, such as a URL where the object is located. Thus, by being actionable and interoperable, a DOI differs from ISBNs or ISRCs which are identifiers only. The DOI system uses the indecs Content Model for representing metadata. The DOI for a document remains fixed ov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles Jean De La Vallée Poussin
Charles-Jean Étienne Gustave Nicolas, baron de la Vallée Poussin (14 August 1866 – 2 March 1962) was a Belgian mathematician. He is best known for proving the prime number theorem. The king of Belgium ennobled him with the title of baron. Biography De la Vallée Poussin was born in Leuven, Belgium. He studied mathematics at the Catholic University of Leuven under his uncle Louis-Philippe Gilbert, after he had earned his bachelor's degree in engineering. De la Vallée Poussin was encouraged to study for a doctorate in physics and mathematics, and in 1891, at the age of just 25, he became an assistant professor in mathematical analysis. De la Vallée Poussin became a professor at the same university (as was his father, Charles Louis de la Vallée Poussin, who taught mineralogy and geology) in 1892. De la Vallée Poussin was awarded with Gilbert's chair when Gilbert died. While he was a professor there, de la Vallée Poussin carried out research in mathematical analysis and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
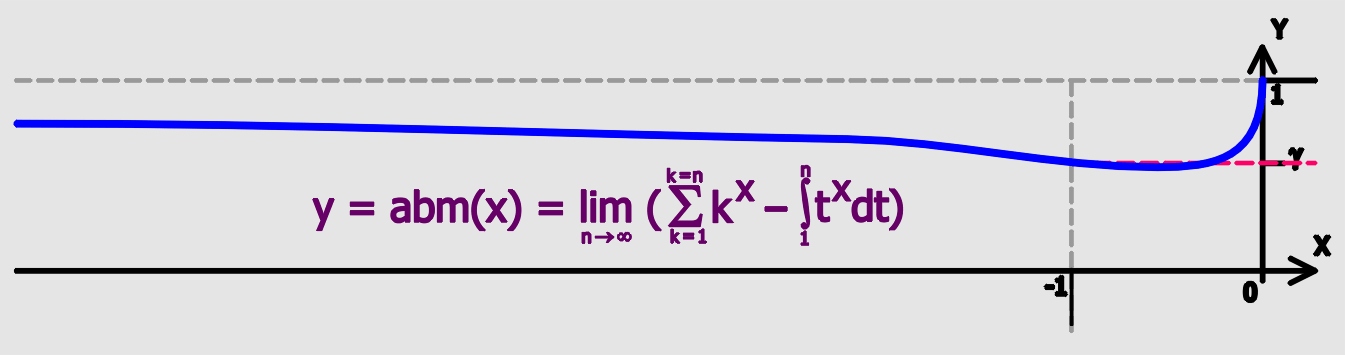
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lebesgue Constant (interpolation)
In mathematics, the Lebesgue constants (depending on a set of nodes and of its size) give an idea of how good the interpolant of a function (at the given nodes) is in comparison with the best polynomial approximation of the function (the degree of the polynomials are fixed). The Lebesgue constant for polynomials of degree at most and for the set of nodes is generally denoted by . These constants are named after Henri Lebesgue. Definition We fix the interpolation nodes x_0, ..., x_nand an interval ,\,b/math> containing all the interpolation nodes. The process of interpolation maps the function f to a polynomial p. This defines a mapping X from the space ''C''( 'a'', ''b'' of all continuous functions on 'a'', ''b''to itself. The map ''X'' is linear and it is a projection on the subspace of polynomials of degree or less. The Lebesgue constant \Lambda_n(T) is defined as the operator norm of ''X''. This definition requires us to specify a norm on ''C''( 'a'', ''b''. The unif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Space
In approximation theory, a Haar space or Chebyshev space is a finite-dimensional subspace V of \mathcal C(X, \mathbb K), where X is a compact space and \mathbb K either the real numbers or the complex numbers, such that for any given f \in \mathcal C(X, \mathbb K) there is exactly one element of V that approximates f "best", i.e. with minimum distance to f in supremum norm In mathematical analysis, the uniform norm (or ) assigns to real- or complex-valued bounded functions defined on a set the non-negative number :\, f\, _\infty = \, f\, _ = \sup\left\. This norm is also called the , the , the , or, when the .... References Approximation theory {{mathanalysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimax Approximation Algorithm
A minimax approximation algorithm (or L∞ approximation or uniform approximation) is a method to find an approximation of a mathematical function that minimizes maximum error. For example, given a function f defined on the interval ,b/math> and a degree bound n, a minimax polynomial approximation algorithm will find a polynomial p of degree at most n to minimize ::\max_, f(x)-p(x), . Polynomial approximations The Weierstrass approximation theorem states that every continuous function defined on a closed interval ,bcan be uniformly approximated as closely as desired by a polynomial function. For practical work it is often desirable to minimize the maximum absolute or relative error of a polynomial fit for any given number of terms in an effort to reduce computational expense of repeated evaluation. Polynomial expansions such as the Taylor series expansion are often convenient for theoretical work but less useful for practical applications. Truncated Chebyshev series, however, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
