|
Relative Change And Difference
In any quantitative science, the terms relative change and relative difference are used to compare two quantities while taking into account the "sizes" of the things being compared, i.e. dividing by a ''standard'' or ''reference'' or ''starting'' value. The comparison is expressed as a ratio and is a unitless number. By multiplying these ratios by 100 they can be expressed as percentages so the terms percentage change, percent(age) difference, or relative percentage difference are also commonly used. The terms "change" and "difference" are used interchangeably. Relative change is often used as a quantitative indicator of quality assurance and quality control for repeated measurements where the outcomes are expected to be the same. A special case of percent change (relative change expressed as a percentage) called ''percent error'' occurs in measuring situations where the reference value is the accepted or actual value (perhaps theoretically determined) and the value being compared ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantitative Science
The exact sciences, sometimes called the exact mathematical sciences, are those sciences "which admit of absolute precision in their results"; especially the mathematical sciences. Examples of the exact sciences are mathematics, optics, astronomy, and physics, which many philosophers from Descartes, Leibniz, and Kant to the logical positivists took as paradigms of rational and objective knowledge. These sciences have been practiced in many cultures from antiquity to modern times. Given their ties to mathematics, the exact sciences are characterized by accurate quantitative expression, precise predictions and/or rigorous methods of testing hypotheses involving quantifiable predictions and measurements. The distinction between the quantitative exact sciences and those sciences that deal with the causes of things is due to Aristotle, who distinguished mathematics from natural philosophy and considered the exact sciences to be the "more natural of the branches of mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martians
Mars, the fourth planet from the Sun, has appeared as a setting in works of fiction since at least the mid-1600s. It became the most popular celestial object in fiction in the late 1800s as the Moon was evidently lifeless. At the time, the predominant genre depicting Mars was utopian fiction. Contemporaneously, the mistaken belief that there are canals on Mars emerged and made its way into fiction. ''The War of the Worlds'', H. G. Wells' story of an alien invasion of Earth by sinister Martians, was published in 1897 and went on to have a large influence on the science fiction genre. Life on Mars appeared frequently in fiction throughout the first half of the 1900s. Apart from enlightened as in the utopian works from the turn of the century, or evil as in the works inspired by Wells, intelligent and human-like Martians also began to be depicted as decadent, a portrayal that was popularized by Edgar Rice Burroughs in the '' Barsoom'' series and adopted by Leigh Brackett am ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Scale
A logarithmic scale (or log scale) is a way of displaying numerical data over a very wide range of values in a compact way—typically the largest numbers in the data are hundreds or even thousands of times larger than the smallest numbers. Such a scale is nonlinear: the numbers 10 and 20, and 60 and 70, are not the same distance apart on a log scale. Rather, the numbers 10 and 100, and 60 and 600 are equally spaced. Thus moving a unit of distance along the scale means the number has been ''multiplied'' by 10 (or some other fixed factor). Often exponential growth curves are displayed on a log scale, otherwise they would increase too quickly to fit within a small graph. Another way to think about it is that the ''number of digits'' of the data grows at a constant rate. For example, the numbers 10, 100, 1000, and 10000 are equally spaced on a log scale, because their numbers of digits is going up by 1 each time: 2, 3, 4, and 5 digits. In this way, adding two digits ''multiplies'' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Standard Deviation
In probability theory and statistics, the coefficient of variation (CV), also known as relative standard deviation (RSD), is a standardized measure of dispersion of a probability distribution or frequency distribution. It is often expressed as a percentage, and is defined as the ratio of the standard deviation \sigma to the mean \mu (or its absolute value, The CV or RSD is widely used in analytical chemistry to express the precision and repeatability of an assay. It is also commonly used in fields such as engineering or physics when doing quality assurance studies and ANOVA gauge R&R, by economists and investors in economic models, and in neuroscience. Definition The coefficient of variation (CV) is defined as the ratio of the standard deviation \ \sigma to the mean \ \mu , c_ = \frac. It shows the extent of variability in relation to the mean of the population. The coefficient of variation should be computed only for data measured on scales that have a meaningful z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Errors And Residuals In Statistics
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its " true value" (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the '' estimated'' value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals. In econometrics, "errors" are also called disturbances. Introduction Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Error
The approximation error in a data value is the discrepancy between an exact value and some ''approximation'' to it. This error can be expressed as an absolute error (the numerical amount of the discrepancy) or as a relative error (the absolute error divided by the data value). An approximation error can occur because of computing machine precision or measurement error (e.g. the length of a piece of paper is 4.53 cm but the ruler only allows you to estimate it to the nearest 0.1 cm, so you measure it as 4.5 cm). In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm. Formal definition One commonly distinguishes between the relative error and the absolute error. Given some value ''v'' and its approximation ''v''approx, the absolute error is :\epsilon = , v-v_\text, \ , where the vertical bars denote the absolute value. If v \ne 0, the relative error is : \eta = \frac = \left, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit From Above
In calculus, a one-sided limit refers to either one of the two limits of a function f(x) of a real variable x as x approaches a specified point either from the left or from the right. The limit as x decreases in value approaching a (x approaches a "from the right" or "from above") can be denoted: \lim_f(x) \quad \text \quad \lim_\,f(x) \quad \text \quad \lim_\,f(x) \quad \text \quad f(x+) The limit as x increases in value approaching a (x approaches a "from the left" or "from below") can be denoted: \lim_f(x) \quad \text \quad \lim_\, f(x) \quad \text \quad \lim_\,f(x) \quad \text \quad f(x-) If the limit of f(x) as x approaches a exists then the limits from the left and from the right both exist and are equal. In some cases in which the limit \lim_ f(x) does not exist, the two one-sided limits nonetheless exist. Consequently, the limit as x approaches a is sometimes called a "two-sided limit". It is possible for exactly one of the two one-sided limits to exist (while t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), and For example, the absolute value of 3 and the absolute value of −3 is The absolute value of a number may be thought of as its distance from zero. Generalisations of the absolute value for real numbers occur in a wide variety of mathematical settings. For example, an absolute value is also defined for the complex numbers, the quaternions, ordered rings, fields and vector spaces. The absolute value is closely related to the notions of magnitude, distance, and norm in various mathematical and physical contexts. Terminology and notation In 1806, Jean-Robert Argand introduced the term ''module'', meaning ''unit of measure'' in French, specifically for the ''complex'' absolute value, Oxford English Dictionary, Draft Revision, Ju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neper
The neper (symbol: Np) is a logarithmic unit for ratios of measurements of physical field and power quantities, such as gain and loss of electronic signals. The unit's name is derived from the name of John Napier, the inventor of logarithms. As is the case for the decibel and bel, the neper is a unit defined in the international standard ISO 80000. It is not part of the International System of Units (SI), but is accepted for use alongside the SI. Definition Like the decibel, the neper is a unit in a logarithmic scale. While the bel uses the decadic (base-10) logarithm to compute ratios, the neper uses the natural logarithm, based on Euler's number (). The level a ratio of two signal amplitudes or root-power quantities, with the unit neper, is given by : L = \ln\frac\mathrm, where x_1 and x_2 are the signal amplitudes, and is the natural logarithm. The level of a ratio of two power quantities, with the unit neper, is given by : L = \frac \ln\frac\mathrm, where p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
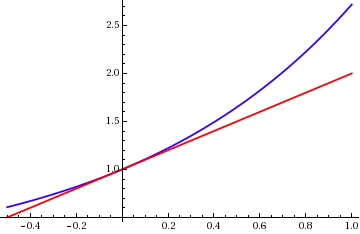
Natural Logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if the base is implicit, simply . Parentheses are sometimes added for clarity, giving , , or . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. The natural logarithm of is the power to which would have to be raised to equal . For example, is , because . The natural logarithm of itself, , is , because , while the natural logarithm of is , since . The natural logarithm can be defined for any positive real number as the area under the curve from to (with the area being negative when ). The simplicity of this definition, which is matched in many other formulas involving the natural logarithm, leads to the term "natural". The definition of the natural logarithm can the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Error
The approximation error in a data value is the discrepancy between an exact value and some ''approximation'' to it. This error can be expressed as an absolute error (the numerical amount of the discrepancy) or as a relative error (the absolute error divided by the data value). An approximation error can occur because of computing machine precision or measurement error (e.g. the length of a piece of paper is 4.53 cm but the ruler only allows you to estimate it to the nearest 0.1 cm, so you measure it as 4.5 cm). In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm. Formal definition One commonly distinguishes between the relative error and the absolute error. Given some value ''v'' and its approximation ''v''approx, the absolute error is :\epsilon = , v-v_\text, \ , where the vertical bars denote the absolute value. If v \ne 0, the relative error is : \eta = \frac = \left, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equality (mathematics)
In mathematics, equality is a relationship between two quantities or, more generally two mathematical expressions, asserting that the quantities have the same value, or that the expressions represent the same mathematical object. The equality between and is written , and pronounced equals . The symbol "" is called an "equals sign". Two objects that are not equal are said to be distinct. For example: * x=y means that and denote the same object. * The identity (x+1)^2=x^2+2x+1 means that if is any number, then the two expressions have the same value. This may also be interpreted as saying that the two sides of the equals sign represent the same function. * \ = \ if and only if P(x) \Leftrightarrow Q(x). This assertion, which uses set-builder notation, means that if the elements satisfying the property P(x) are the same as the elements satisfying Q(x), then the two uses of the set-builder notation define the same set. This property is often expressed as "two sets that have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |