|
Quasi Zenith Satellite System
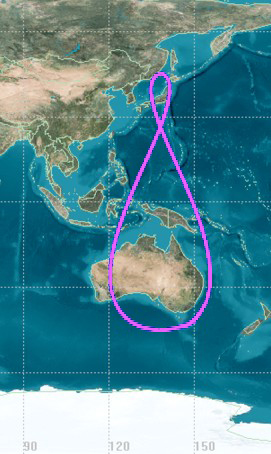
The Quasi-Zenith Satellite System (QZSS), also known as , is a four-satellite regional time transfer system and a satellite-based augmentation system developed by the Japanese government to enhance the United States-operated Global Positioning System (GPS) in the Asia-Oceania regions, with a focus on Japan. The goal of QZSS is to provide highly precise and stable positioning services in the Asia-Oceania region, compatible with GPS. Four-satellite QZSS services were available on a trial basis as of 12 January 2018, and officially started on 1 November 2018. A satellite navigation system independent of GPS is planned for 2023 with 7 satellites. History In 2002, the Japanese government authorized the development of QZSS, as a three-satellite regional time transfer system and a satellite-based augmentation system for the United States operated Global Positioning System (GPS) to be receivable within Japan. A contract was awarded to Advanced Space Business Corporation (ASBC), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
QZSS Logo
The Quasi-Zenith Satellite System (QZSS), also known as , is a four-satellite regional time transfer system and a satellite-based augmentation system developed by the Japanese government to enhance the United States-operated Global Positioning System (GPS) in the Asia-Oceania regions, with a focus on Japan. The goal of QZSS is to provide highly precise and stable positioning services in the Asia-Oceania region, compatible with GPS. Four-satellite QZSS services were available on a trial basis as of 12 January 2018, and officially started on 1 November 2018. A satellite navigation system independent of GPS is planned for 2023 with 7 satellites. History In 2002, the Japanese government authorized the development of QZSS, as a three-satellite regional time transfer system and a satellite-based augmentation system for the United States operated Global Positioning System (GPS) to be receivable within Japan. A contract was awarded to Advanced Space Business Corporation (ASBC), th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
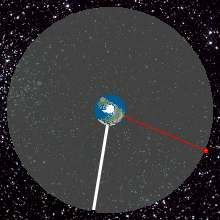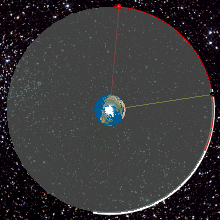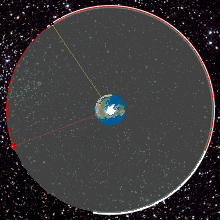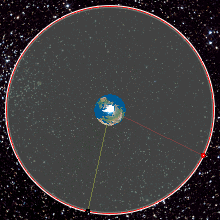
Geostationary Orbit
A geostationary orbit, also referred to as a geosynchronous equatorial orbit''Geostationary orbit'' and ''Geosynchronous (equatorial) orbit'' are used somewhat interchangeably in sources. (GEO), is a circular geosynchronous orbit in altitude above Earth's equator ( in radius from Earth's center) and following the direction of Earth's rotation. An object in such an orbit has an orbital period equal to Earth's rotational period, one sidereal day, and so to ground observers it appears motionless, in a fixed position in the sky. The concept of a geostationary orbit was popularised by the science fiction writer Arthur C. Clarke in the 1940s as a way to revolutionise telecommunications, and the first satellite to be placed in this kind of orbit was launched in 1963. Communications satellites are often placed in a geostationary orbit so that Earth-based satellite antennas do not have to rotate to track them but can be pointed permanently at the position in the sky where the sat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geostationary Orbit
A geostationary orbit, also referred to as a geosynchronous equatorial orbit''Geostationary orbit'' and ''Geosynchronous (equatorial) orbit'' are used somewhat interchangeably in sources. (GEO), is a circular geosynchronous orbit in altitude above Earth's equator ( in radius from Earth's center) and following the direction of Earth's rotation. An object in such an orbit has an orbital period equal to Earth's rotational period, one sidereal day, and so to ground observers it appears motionless, in a fixed position in the sky. The concept of a geostationary orbit was popularised by the science fiction writer Arthur C. Clarke in the 1940s as a way to revolutionise telecommunications, and the first satellite to be placed in this kind of orbit was launched in 1963. Communications satellites are often placed in a geostationary orbit so that Earth-based satellite antennas do not have to rotate to track them but can be pointed permanently at the position in the sky where the sat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Anomaly
In celestial mechanics, the mean anomaly is the fraction of an elliptical orbit's period that has elapsed since the orbiting body passed periapsis, expressed as an angle which can be used in calculating the position of that body in the classical two-body problem. It is the angular distance from the pericenter which a fictitious body would have if it moved in a circular orbit, with constant speed, in the same orbital period as the actual body in its elliptical orbit. Definition Define as the time required for a particular body to complete one orbit. In time , the radius vector sweeps out 2 radians, or 360°. The average rate of sweep, , is then :n = \frac = \frac~, which is called the '' mean angular motion'' of the body, with dimensions of radians per unit time or degrees per unit time. Define as the time at which the body is at the pericenter. From the above definitions, a new quantity, , the ''mean anomaly'' can be defined :M = n\,(t - \tau) ~, which gives an angular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
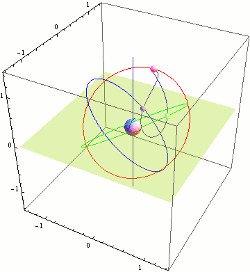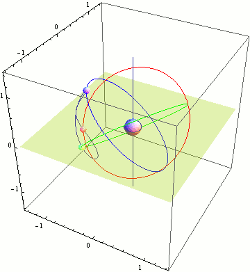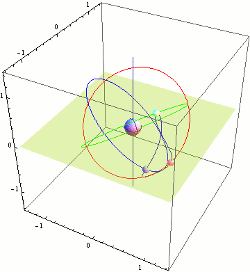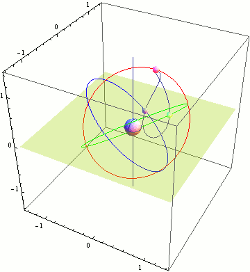
Argument Of Perigee
The argument of periapsis (also called argument of perifocus or argument of pericenter), symbolized as ''ω'', is one of the orbital elements of an orbiting body. Parametrically, ''ω'' is the angle from the body's ascending node to its periapsis, measured in the direction of motion. For specific types of orbits, terms such as argument of perihelion (for heliocentric orbits), argument of perigee (for geocentric orbits), argument of periastron (for orbits around stars), and so on, may be used (see apsis for more information). An argument of periapsis of 0° means that the orbiting body will be at its closest approach to the central body at the same moment that it crosses the plane of reference from South to North. An argument of periapsis of 90° means that the orbiting body will reach periapsis at its northmost distance from the plane of reference. Adding the argument of periapsis to the longitude of the ascending node gives the longitude of the periapsis. However, especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Ascension Of The Ascending Node
The longitude of the ascending node (☊ or Ω) is one of the orbital elements used to specify the orbit of an object in space. It is the angle from a specified reference direction, called the ''origin of longitude'', to the direction of the ascending node, as measured in a specified reference plane. The ascending node is the point where the orbit of the object passes through the plane of reference, as seen in the adjacent image. Commonly used reference planes and origins of longitude include: * For geocentric orbits, Earth's equatorial plane as the reference plane, and the First Point of Aries as the origin of longitude. In this case, the longitude is also called the right ascension of the ascending node (RAAN). The angle is measured eastwards (or, as seen from the north, counterclockwise) from the First Point of Aries to the node. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inclination
Orbital inclination measures the tilt of an object's orbit around a celestial body. It is expressed as the angle between a Plane of reference, reference plane and the orbital plane or Axis of rotation, axis of direction of the orbiting object. For a satellite orbiting the Earth directly above the Equator, the plane of the satellite's orbit is the same as the Earth's equatorial plane, and the satellite's orbital inclination is 0°. The general case for a circular orbit is that it is tilted, spending half an orbit over the northern hemisphere and half over the southern. If the orbit swung between 20° north latitude and 20° south latitude, then its orbital inclination would be 20°. Orbits The inclination is one of the six orbital elements describing the shape and orientation of a celestial orbit. It is the angle between the orbital plane and the plane of reference, normally stated in degree (angle), degrees. For a satellite orbiting a planet, the plane of reference is usually ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eccentricity (orbit)
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * circular orbit: ''e'' = 0 * elliptic orbit: 0 < ''e'' < 1 * [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semimajor Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinated Universal Time
Coordinated Universal Time or UTC is the primary time standard by which the world regulates clocks and time. It is within about one second of mean solar time (such as UT1) at 0° longitude (at the IERS Reference Meridian as the currently used prime meridian) and is not adjusted for daylight saving time. It is effectively a successor to Greenwich Mean Time (GMT). The coordination of time and frequency transmissions around the world began on 1 January 1960. UTC was first officially adopted as CCIR Recommendation 374, ''Standard-Frequency and Time-Signal Emissions'', in 1963, but the official abbreviation of UTC and the official English name of Coordinated Universal Time (along with the French equivalent) were not adopted until 1967. The system has been adjusted several times, including a brief period during which the time-coordination radio signals broadcast both UTC and "Stepped Atomic Time (SAT)" before a new UTC was adopted in 1970 and implemented in 1972. This change also a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epoch (astronomy)
In astronomy, an epoch or reference epoch is a moment in time used as a reference point for some time-varying astronomical quantity. It is useful for the celestial coordinates or orbital elements of a celestial body, as they are subject to perturbations and vary with time. These time-varying astronomical quantities might include, for example, the mean longitude or mean anomaly of a body, the node of its orbit relative to a reference plane, the direction of the apogee or aphelion of its orbit, or the size of the major axis of its orbit. The main use of astronomical quantities specified in this way is to calculate other relevant parameters of motion, in order to predict future positions and velocities. The applied tools of the disciplines of celestial mechanics or its subfield orbital mechanics (for predicting orbital paths and positions for bodies in motion under the gravitational effects of other bodies) can be used to generate an ephemeris, a table of values giving the posit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Elements
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes, each consisting of a set of six parameters, are commonly used in astronomy and orbital mechanics. A real orbit and its elements change over time due to gravitational perturbations by other objects and the effects of general relativity. A Kepler orbit is an idealized, mathematical approximation of the orbit at a particular time. Keplerian elements The traditional orbital elements are the six Keplerian elements, after Johannes Kepler and his laws of planetary motion. When viewed from an inertial frame, two orbiting bodies trace out distinct trajectories. Each of these trajectories has its focus at the common center of mass. When viewed from a non-inertial frame centered on one of the bodies, only the traj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |