|
Probably Approximately Correct Learning
In computational learning theory, probably approximately correct (PAC) learning is a framework for mathematical analysis of machine learning. It was proposed in 1984 by Leslie Valiant.L. Valiant. A theory of the learnable.' Communications of the ACM, 27, 1984. In this framework, the learner receives samples and must select a generalization function (called the ''hypothesis'') from a certain class of possible functions. The goal is that, with high probability (the "probably" part), the selected function will have low generalization error (the "approximately correct" part). The learner must be able to learn the concept given any arbitrary approximation ratio, probability of success, or distribution of the samples. The model was later extended to treat noise (misclassified samples). An important innovation of the PAC framework is the introduction of computational complexity theory concepts to machine learning. In particular, the learner is expected to find efficient functions (t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computational Learning Theory
In computer science, computational learning theory (or just learning theory) is a subfield of artificial intelligence devoted to studying the design and analysis of machine learning algorithms. Overview Theoretical results in machine learning mainly deal with a type of inductive learning called supervised learning. In supervised learning, an algorithm is given samples that are labeled in some useful way. For example, the samples might be descriptions of mushrooms, and the labels could be whether or not the mushrooms are edible. The algorithm takes these previously labeled samples and uses them to induce a classifier. This classifier is a function that assigns labels to samples, including samples that have not been seen previously by the algorithm. The goal of the supervised learning algorithm is to optimize some measure of performance such as minimizing the number of mistakes made on new samples. In addition to performance bounds, computational learning theory studies the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Morphological Skeleton
In digital image processing, morphological skeleton is a Topological skeleton, skeleton (or medial axis) representation of a shape or binary image, computed by means of mathematical morphology, morphological operators. Morphological skeletons are of two kinds: * Those defined by means of opening (morphology), morphological openings, from which the original shape can be reconstructed, * Those computed by means of the hit-or-miss transform, which preserve the shape's topology. Skeleton by openings Lantuéjoul's formula Continuous images In (#lantuejoul77, Lantuéjoul 1977),See also (#serra82, Serra's 1982 book) Christian Lantuéjoul, Lantuéjoul derived the following morphological formula for the skeleton of a continuous binary image X\subset \mathbb^2: :S(X)=\bigcup_\bigcap_\left[(X\ominus \rho B)-(X\ominus \rho B)\circ \mu \overline B\right], where \ominus and \circ are the morphological erosion (morphology), erosion and opening (morphology), opening, respectively, \rho B is an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Error Tolerance (PAC Learning)
In PAC learning, error tolerance refers to the ability of an algorithm to learn when the examples received have been corrupted in some way. In fact, this is a very common and important issue since in many applications it is not possible to access noise-free data. Noise can interfere with the learning process at different levels: the algorithm may receive data that have been occasionally mislabeled, or the inputs may have some false information, or the classification of the examples may have been maliciously adulterated. Notation and the Valiant learning model In the following, let X be our n-dimensional input space. Let \mathcal be a class of functions that we wish to use in order to learn a \-valued target function f defined over X. Let \mathcal be the distribution of the inputs over X. The goal of a learning algorithm \mathcal is to choose the best function h \in \mathcal such that it minimizes error(h) = P_( h(x) \neq f(x)). Let us suppose we have a function size(f) that can me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Data Mining
Data mining is the process of extracting and finding patterns in massive data sets involving methods at the intersection of machine learning, statistics, and database systems. Data mining is an interdisciplinary subfield of computer science and statistics with an overall goal of extracting information (with intelligent methods) from a data set and transforming the information into a comprehensible structure for further use. Data mining is the analysis step of the " knowledge discovery in databases" process, or KDD. Aside from the raw analysis step, it also involves database and data management aspects, data pre-processing, model and inference considerations, interestingness metrics, complexity considerations, post-processing of discovered structures, visualization, and online updating. The term "data mining" is a misnomer because the goal is the extraction of patterns and knowledge from large amounts of data, not the extraction (''mining'') of data itself. It also is a buzzwo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Occam Learning
In computational learning theory, Occam learning is a model of algorithmic learning where the objective of the learner is to output a succinct representation of received training data. This is closely related to probably approximately correct (PAC) learning, where the learner is evaluated on its predictive power of a test set. Occam learnability implies PAC learning, and for a wide variety of concept classes, the converse is also true: PAC learnability implies Occam learnability. Introduction Occam Learning is named after Occam's razor, which is a principle stating that, given all other things being equal, a shorter explanation for observed data should be favored over a lengthier explanation. The theory of Occam learning is a formal and mathematical justification for this principle. It was first shown by Blumer, et al. that Occam learning implies PAC learning, which is the standard model of learning in computational learning theory. In other words, ''parsimony'' (of the output ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Compressible (Littlestone And Warmuth)
In thermodynamics and fluid mechanics, the compressibility (also known as the coefficient of compressibility or, if the temperature is held constant, the isothermal compressibility) is a measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure (or mean stress) change. In its simple form, the compressibility \kappa (denoted in some fields) may be expressed as :\beta =-\frac\frac, where is volume and is pressure. The choice to define compressibility as the negative of the fraction makes compressibility positive in the (usual) case that an increase in pressure induces a reduction in volume. The reciprocal of compressibility at fixed temperature is called the isothermal bulk modulus. Definition The specification above is incomplete, because for any object or system the magnitude of the compressibility depends strongly on whether the process is isentropic or isothermal. Accordingly, isothermal compressibility is defined: :\beta_T=-\fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
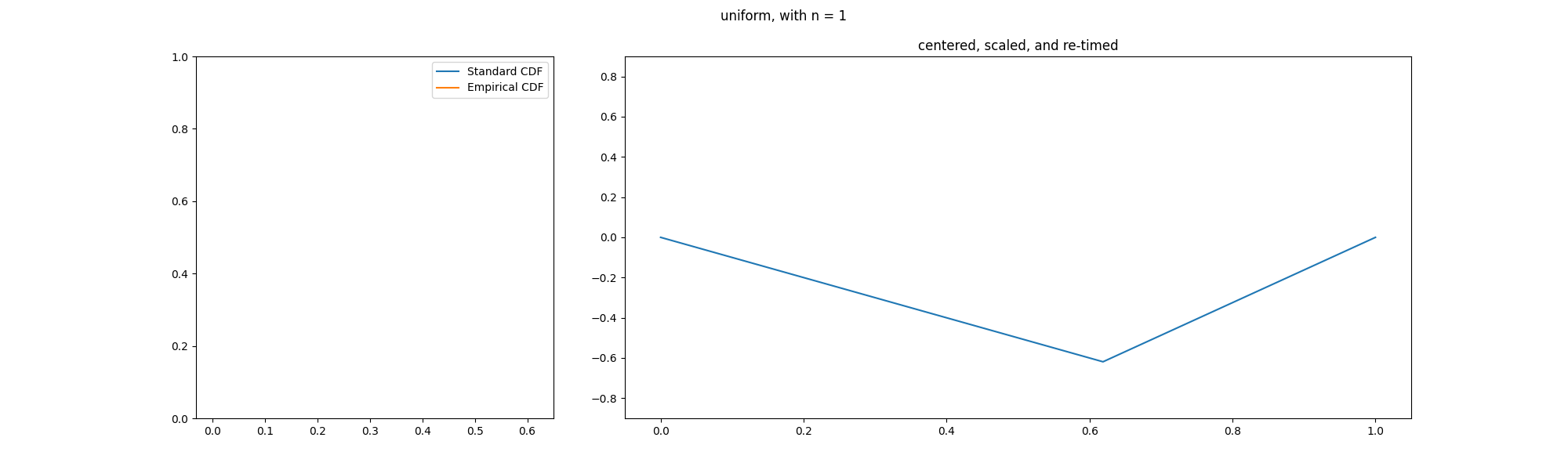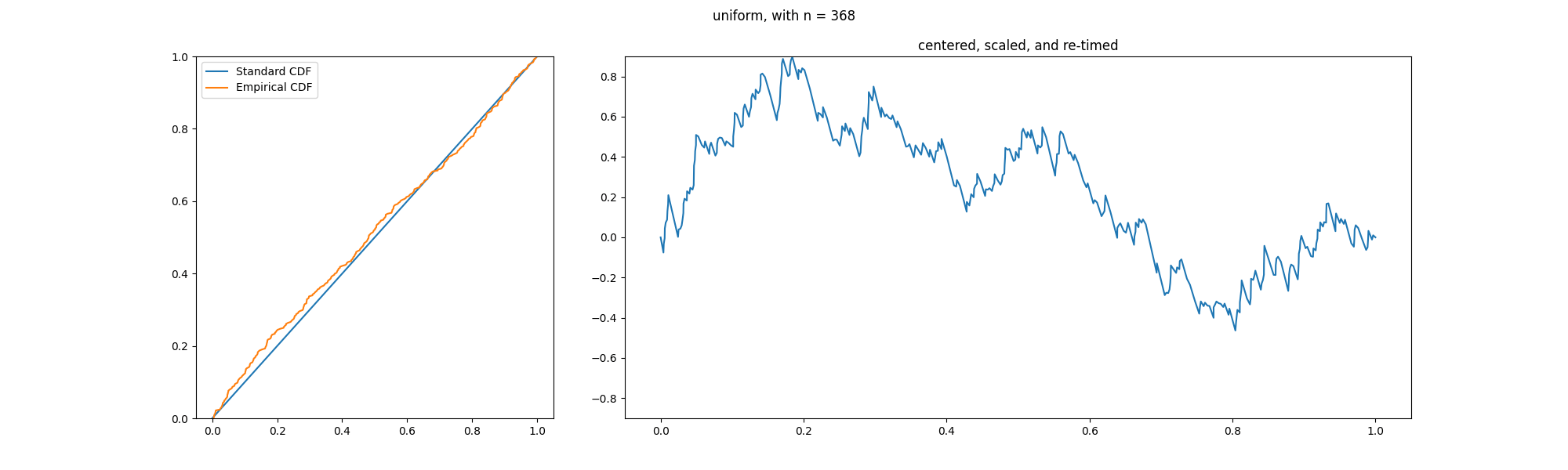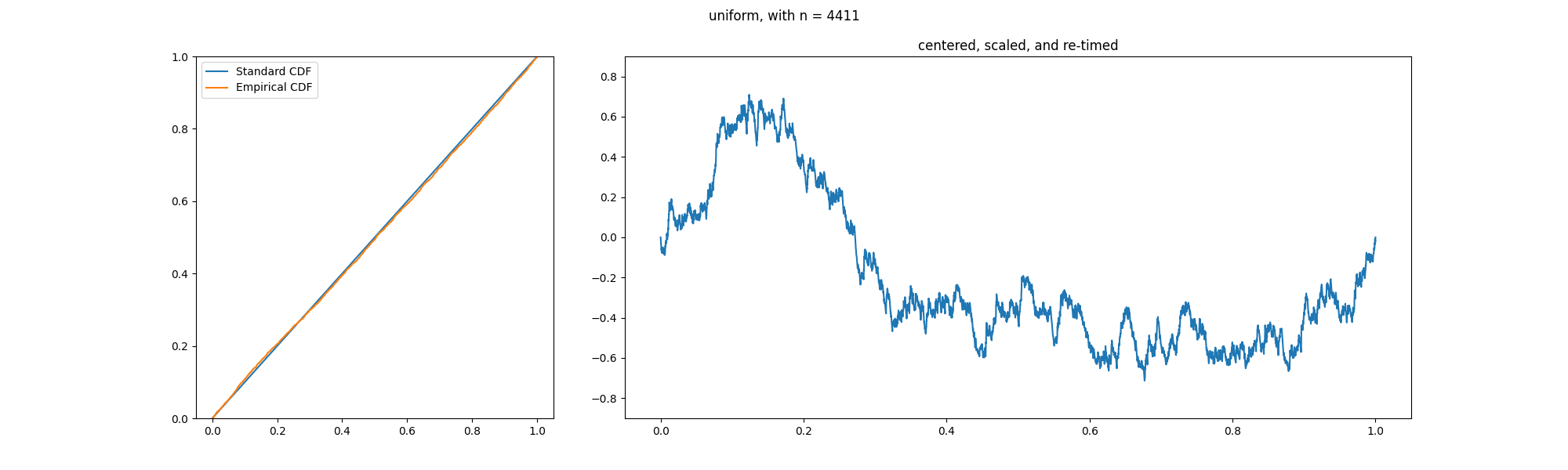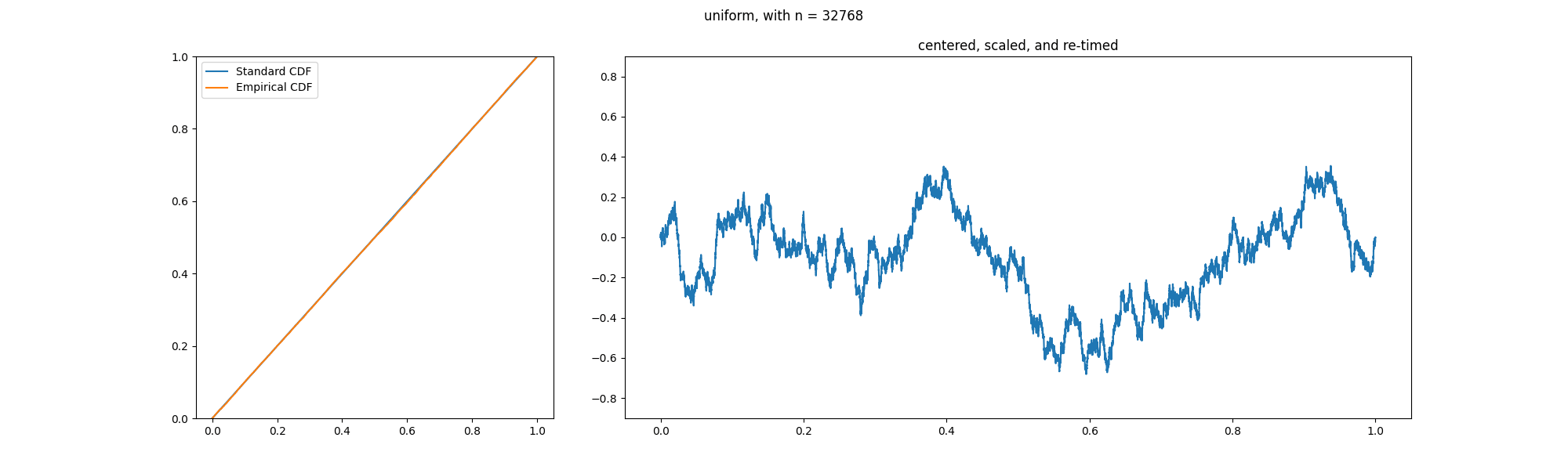
Glivenko–Cantelli Theorem
In the theory of probability, the Glivenko–Cantelli theorem (sometimes referred to as the fundamental theorem of statistics), named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, describes the asymptotic behaviour of the empirical distribution function as the number of Independent and identically distributed random variables, independent and identically distributed observations grows. Specifically, the empirical distribution function Uniform convergence, converges uniformly to the true distribution function almost surely. The uniform convergence of more general empirical measures becomes an important property of the Glivenko–Cantelli classes of functions or sets. The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning. Applications can be found in econometrics making use of M-estimators. Statement Assume that X_1,X_2,\dots are independent and identically distributed random variables in \mathbb with commo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
VC Dimension
VC may refer to: Military decorations * Victoria Cross, a military decoration awarded by the United Kingdom and other Commonwealth nations ** Victoria Cross for Australia ** Victoria Cross (Canada) ** Victoria Cross for New Zealand * Victorious Cross, Idi Amin's self-bestowed military decoration Organisations * Ocean Airlines (IATA airline designator 2003-2008), Italian cargo airline * Voyageur Airways (IATA airline designator since 1968), Canadian charter airline * Visual Communications, an Asian-Pacific-American media arts organization in Los Angeles, California * Viet Cong, a political and military organization during the Vietnam War (1959–1975) Education * Vanier College, Canada * Vassar College, US * Velez College, Philippines * Virginia College, US * Ventura College, US Places * Saint Vincent and the Grenadines (ISO country code) * Sri Lanka (ICAO airport prefix code) * Watsonian vice-counties, subdivisions of Great Britain or Ireland * Ventura County, in S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pixel Connectivity
In image processing, pixel connectivity is the way in which pixels in 2-dimensional (or hypervoxels in n-dimensional) images relate to their neighbors. Formulation In order to specify a set of connectivities, the dimension and the width of the neighborhood , must be specified. The dimension of a neighborhood is valid for any dimension n\geq1. A common width is 3, which means along each dimension, the central cell will be adjacent to 1 cell on either side for all dimensions. Let M_N^n represent a N-dimensional hypercubic neighborhood with size on each dimension of n=2k+1, k\in\mathbb Let \vec represent a discrete vector in the first orthant from the center structuring element to a point on the boundary of M_N^n. This implies that each element q_i \in \ ,\forall i \in \ and that at least one component q_i = k Let S_N^d represent a N-dimensional hypersphere with radius of d=\left \Vert \vec \right \Vert. Define the amount of elements on the hypersphere S_N^d within the nei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Concept Class
In computational learning theory in mathematics, a concept over a domain ''X'' is a total Boolean function over ''X''. A concept class is a class of concepts. Concept classes are a subject of computational learning theory. Concept class terminology frequently appears in model theory associated with probably approximately correct (PAC) learning. In this setting, if one takes a set ''Y'' as a set of (classifier output) labels, and ''X'' is a set of examples, the map , i.e. from examples to classifier labels (where and where ''c'' is a subset of ''X''), ''c'' is then said to be a ''concept''. A ''concept class'' is then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Machine Learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task (computing), tasks without explicit Machine code, instructions. Within a subdiscipline in machine learning, advances in the field of deep learning have allowed Neural network (machine learning), neural networks, a class of statistical algorithms, to surpass many previous machine learning approaches in performance. ML finds application in many fields, including natural language processing, computer vision, speech recognition, email filtering, agriculture, and medicine. The application of ML to business problems is known as predictive analytics. Statistics and mathematical optimisation (mathematical programming) methods comprise the foundations of machine learning. Data mining is a related field of study, focusing on exploratory data analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Real Numbers
In mathematics, a real number is a number that can be used to measurement, measure a continuous variable, continuous one-dimensional quantity such as a time, duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limit (mathematics), limits, continuous function, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally mathematical notation, denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction (mathematics), fraction . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |