|
Prismatoid Polyhedra
In geometry, a prismatoid is a polyhedron whose vertices all lie in two parallel planes. Its lateral faces can be trapezoids or triangles. If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid. Volume If the areas of the two parallel faces are and , the cross-sectional area of the intersection of the prismatoid with a plane midway between the two parallel faces is , and the height (the distance between the two parallel faces) is , then the volume of the prismatoid is given by V = \fracB. E. Meserve, R. E. Pingry: ''Some Notes on the Prismoidal Formula''. The Mathematics Teacher, Vol. 45, No. 4 (April 1952), pp. 257-263 (This formula follows immediately by integrating the area parallel to the two planes of vertices by Simpson's rule, since that rule is exact for integration of polynomials of degree up to 3, and in this case the area is at most a quadratic function in the height.) Prismatoid famil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prismatoid (parameters H,A₁,A₂,A₃)
In geometry, a prismatoid is a polyhedron whose vertices all lie in two parallel planes. Its lateral faces can be trapezoids or triangles. If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid. Volume If the areas of the two parallel faces are and , the cross-sectional area of the intersection of the prismatoid with a plane midway between the two parallel faces is , and the height (the distance between the two parallel faces) is , then the volume of the prismatoid is given by V = \fracB. E. Meserve, R. E. Pingry: ''Some Notes on the Prismoidal Formula''. The Mathematics Teacher, Vol. 45, No. 4 (April 1952), pp. 257-263 (This formula follows immediately by integrating the area parallel to the two planes of vertices by Simpson's rule, since that rule is exact for integration of polynomials of degree up to 3, and in this case the area is at most a quadratic function in the height.) Prismatoid fam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprism
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History At the intersection of modern-day graph theory and coding theory, the triangulation of a set of points have interested mathematicians since Isaac Newton, who fruitlessly sought a mathematical proof of the kissing number problem in 1694. The existence of antiprisms was discussed, and their name was coined by Johannes Kepler, though it is possible that they were previously known to Archimedes, as they satisfy the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cupola (geometry)
In geometry, a cupola is a solid formed by joining two polygons, one (the base) with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively. A cupola can be seen as a prism where one of the polygons has been collapsed in half by merging alternate vertices. A cupola can be given an extended Schläfli symbol representing a regular polygon joined by a parallel of its truncation, or Cupolae are a subclass of the prismatoids. Its dual contains a shape that is sort of a weld between half of an -sided trapezohedron and a -sided pyramid. Examples The above-mentioned three polyhedra are the only non-trivial convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star Antiprism
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History At the intersection of modern-day graph theory and coding theory, the triangulation of a set of points have interested mathematicians since Isaac Newton, who fruitlessly sought a mathematical proof of the kissing number problem in 1694. The existence of antiprisms was discussed, and their name was coined by Johannes Kepler, though it is possible that they were previously known to Archimedes, as they satisf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Frustum
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°. A pentagon may be simple or self-intersecting. A self-intersecting ''regular pentagon'' (or ''star pentagon'') is called a pentagram. Regular pentagons A '' regular pentagon'' has Schläfli symbol and interior angles of 108°. A '' regular pentagon'' has five lines of reflectional symmetry, and rotational symmetry of order 5 (through 72°, 144°, 216° and 288°). The diagonals of a convex regular pentagon are in the golden ratio to its sides. Given its side length t, its height H (distance from one side to the opposite vertex), width W (distance between two farthest separated points, which equals the diagonal length D) and circumradius R are given by: :\begin H &= \frac~t \approx 1.539~t, \\ W= D &= \frac~t\approx 1.618~t, \\ W &= \sqrt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Cupola
In geometry, the pentagonal cupola is one of the Johnson solids (). It can be obtained as a slice of the rhombicosidodecahedron. The pentagonal cupola consists of 5 equilateral triangles, 5 squares, 1 pentagon, and 1 decagon. Formulae The following formulae for volume, surface area and circumradius can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Pentagonal cupola from Wolfram Alpha. Retrieved April 11, 2020. :V=\left(\frac\left(5+4\sqrt\right)\right)a^3\approx2.32405a^3, :A=\left(\frac\left(20+5\sqrt+\sqrt\right)\right)a^2\approx16.57975a^2, :R=\left(\frac\sqrt\right)a\approx2.23295a. The height of the pentagonal cupola is :h = \sqrta \approx 0.52573a. Related polyhedra Dual polyhedron The dual of the pentagonal cupola has 10 triangular faces and 5 kite faces: Other convex cupolae Crossed pentagrammic cupola In geometry, the crossed pentagrammic cupola is one of the nonconvex Johnson solid isomorphs, being topologically identical to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagrammic Crossed Antiprism
In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams. It differs from the pentagrammic antiprism by having opposite orientations on the two pentagrams. This polyhedron is identified with the indexed name U80 as a uniform polyhedron. The pentagrammic crossed-antiprism may be inscribed within an icosahedron, and has ten triangular faces in common with the great icosahedron. It has the same vertex arrangement as the pentagonal antiprism. In fact, it may be considered as a parabidiminished great icosahedron. See also * Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms. All have their vertices in parallel planes and are therefore prismatoid ... External links * *http://www.mathconsult.ch/sho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces. Hence, it is a non-regular dodecahedron. Geometry If the faces of the pentagonal antiprism are all regular, it is a semiregular polyhedron. It can also be considered as a parabidiminished icosahedron, a shape formed by removing two pentagonal pyramids from a regular icosahedron leaving two nonadjacent pentagonal faces; a related shape, the metabidiminished icosahedron (one of the Johnson solids), is likewise form from the icosahedron by removing two pyramids, but its pentagonal faces are adjacent to each other. The two pentagonal faces of either shape can be augmented with pyramids to form the icosahedron. Relation to polytopes The pentagonal antiprism occurs as a constituent element in some higher-dimensional p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Antiprism
In geometry, the square antiprism is the second in an infinite family of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It is also known as an ''anticube''. If all its faces are regular, it is a semiregular polyhedron or uniform polyhedron. A nonuniform ''D''4-symmetric variant is the cell of the noble square antiprismatic 72-cell. Points on a sphere When eight points are distributed on the surface of a sphere with the aim of maximising the distance between them in some sense, the resulting shape corresponds to a square antiprism rather than a cube. Specific methods of distributing the points include, for example, the Thomson problem (minimizing the sum of all the reciprocals of distances between points), maximising the distance of each point to the nearest point, or minimising the sum of all reciprocals of squares of distances between points. Molecules with square antiprismatic geometry According to the VSEPR theory of molecul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with seven faces, fifteen edges, and ten vertices. As a semiregular (or uniform) polyhedron If faces are all regular, the pentagonal prism is a semiregular polyhedron, more generally, a uniform polyhedron, and the third in an infinite set of prisms formed by square sides and two regular polygon caps. It can be seen as a '' truncated pentagonal hosohedron'', represented by Schläfli symbol t. Alternately it can be seen as the Cartesian product of a regular pentagon and a line segment, and represented by the product ×. The dual of a pentagonal prism is a pentagonal bipyramid. The symmetry group of a right pentagonal prism is ''D5h'' of order 20. The rotation group is ''D5'' of order 10. Volume The volume, as for all prisms, is the product of the area of the pentagonal base times the height or distance along any edge perpendicular to the base. For a uniform pentagonal pris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelepiped 2013-11-29
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, the four concepts—''parallelepiped'' and ''cube'' in three dimensions, ''parallelogram'' and ''square'' in two dimensions—are defined, but in the context of a more general affine geometry, in which angles are not differentiated, only ''parallelograms'' and ''parallelepipeds'' exist. Three equivalent definitions of ''parallelepiped'' are *a polyhedron with six faces (hexahedron), each of which is a parallelogram, *a hexahedron with three pairs of parallel faces, and *a prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all specific cases of parallelepiped. "Parallelepiped" is now usually pronounced or ; trad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
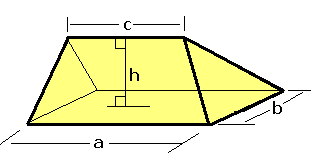
Geometric Wedge
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
