|
Percolation Thresholds
The percolation threshold is a mathematical concept in percolation theory that describes the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist; while above it, there exists a giant component of the order of system size. In engineering and coffee making, percolation represents the flow of fluids through porous media, but in the mathematics and physics worlds it generally refers to simplified lattice models of random systems or networks (graphs), and the nature of the connectivity in them. The percolation threshold is the critical value of the occupation probability ''p'', or more generally a critical surface for a group of parameters ''p''1, ''p''2, ..., such that infinite connectivity (''percolation'') first occurs. Percolation models The most common percolation model is to take a regular lattice, like a square lattice, and make it into a random network by randomly "occupying" sites (vertices) or bonds (edges ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percolation Theory
In statistical physics and mathematics, percolation theory describes the behavior of a network when nodes or links are added. This is a geometric type of phase transition, since at a critical fraction of addition the network of small, disconnected clusters merge into significantly larger connected, so-called spanning clusters. The applications of percolation theory to materials science and in many other disciplines are discussed here and in the articles network theory and percolation. Introduction A representative question (and the source of the name) is as follows. Assume that some liquid is poured on top of some porous material. Will the liquid be able to make its way from hole to hole and reach the bottom? This physical question is modelled mathematically as a three-dimensional network of vertices, usually called "sites", in which the edge or "bonds" between each two neighbors may be open (allowing the liquid through) with probability , or closed with probability , and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Percolation
In statistical physics, directed percolation (DP) refers to a class of models that mimic filtering of fluids through porous materials along a given direction, due to the effect of gravity. Varying the microscopic connectivity of the pores, these models display a phase transition from a macroscopically permeable (percolating) to an impermeable (non-percolating) state. Directed percolation is also used as a simple model for epidemic spreading with a transition between survival and extinction of the disease depending on the infection rate. More generally, the term directed percolation stands for a universality class of continuous phase transitions which are characterized by the same type of collective behavior on large scales. Directed percolation is probably the simplest universality class of transitions out of thermal equilibrium. Lattice models One of the simplest realizations of DP is bond directed percolation. This model is a directed variant of ordinary (isotropic) percol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clustering Coefficient
In graph theory, a clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties; this likelihood tends to be greater than the average probability of a tie randomly established between two nodes (Holland and Leinhardt, 1971; Watts and Strogatz, 1998). Two versions of this measure exist: the global and the local. The global version was designed to give an overall indication of the clustering in the network, whereas the local gives an indication of the embeddedness of single nodes. Local clustering coefficient The local clustering coefficient of a vertex (node) in a graph quantifies how close its neighbours are to being a clique (complete graph). Duncan J. Watts and Steven Strogatz introduced the measure in 1998 to determine whether a graph is a small-world network ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and Statistical independence, independently of the time since the last event. It is named after France, French mathematician Siméon Denis Poisson (; ). The Poisson distribution can also be used for the number of events in other specified interval types such as distance, area, or volume. For instance, a call center receives an average of 180 calls per hour, 24 hours a day. The calls are independent; receiving one does not change the probability of when the next one will arrive. The number of calls received during any minute has a Poisson probability distribution with mean 3: the most likely numbers are 2 and 3 but 1 and 4 are also likely and there is a small probability of it being as low as zero and a very smal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erdős–Rényi Model
In the mathematical field of graph theory, the Erdős–Rényi model is either of two closely related models for generating random graphs or the evolution of a random network. They are named after Hungarian mathematicians Paul Erdős and Alfréd Rényi, who first introduced one of the models in 1959, while Edgar Gilbert introduced the other model contemporaneously and independently of Erdős and Rényi. In the model of Erdős and Rényi, all graphs on a fixed vertex set with a fixed number of edges are equally likely; in the model introduced by Gilbert, also called the Erdős–Rényi–Gilbert model, each edge has a fixed probability of being present or absent, independently of the other edges. These models can be used in the probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs. Definition There are two closely related variants of the Erdős–R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Distribution
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network. Definition The degree of a node in a network (sometimes referred to incorrectly as the connectivity) is the number of connections or edges the node has to other nodes. If a network is directed, meaning that edges point in one direction from one node to another node, then nodes have two different degrees, the in-degree, which is the number of incoming edges, and the out-degree, which is the number of outgoing edges. The degree distribution ''P''(''k'') of a network is then defined to be the fraction of nodes in the network with degree ''k''. Thus if there are ''n'' nodes in total in a network and ''n''''k'' of them have degree ''k'', we have P(k) = \frac. The same information is also sometimes presented in the form of a ''cumulative degree distribution'', the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment (mathematics)
In mathematics, the moments of a function are certain quantitative measures related to the shape of the function's graph. If the function represents mass density, then the zeroth moment is the total mass, the first moment (normalized by total mass) is the center of mass, and the second moment is the moment of inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. The mathematical concept is closely related to the concept of moment in physics. For a distribution of mass or probability on a bounded interval, the collection of all the moments (of all orders, from to ) uniquely determines the distribution (Hausdorff moment problem). The same is not true on unbounded intervals (Hamburger moment problem). In the mid-nineteenth century, Pafnuty Chebyshev became the first person to think systematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Distribution
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network. Definition The degree of a node in a network (sometimes referred to incorrectly as the connectivity) is the number of connections or edges the node has to other nodes. If a network is directed, meaning that edges point in one direction from one node to another node, then nodes have two different degrees, the in-degree, which is the number of incoming edges, and the out-degree, which is the number of outgoing edges. The degree distribution ''P''(''k'') of a network is then defined to be the fraction of nodes in the network with degree ''k''. Thus if there are ''n'' nodes in total in a network and ''n''''k'' of them have degree ''k'', we have P(k) = \frac. The same information is also sometimes presented in the form of a ''cumulative degree distribution'', the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Giant Component
In network theory, a giant component is a connected component of a given random graph that contains a finite fraction of the entire graph's vertices. Giant component in Erdős–Rényi model Giant components are a prominent feature of the Erdős–Rényi model (ER) of random graphs, in which each possible edge connecting pairs of a given set of vertices is present, independently of the other edges, with probability . In this model, if p \le \frac for any constant \epsilon>0, then with high probability all connected components of the graph have size , and there is no giant component. However, for p \ge \frac there is with high probability a single giant component, with all other components having size . For p=p_c = \frac, intermediate between these two possibilities, the number of vertices in the largest component of the graph, P_ is with high probability proportional to n^.. Giant component is also important in percolation theory. When a fraction of nodes, q=1-p, is removed ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
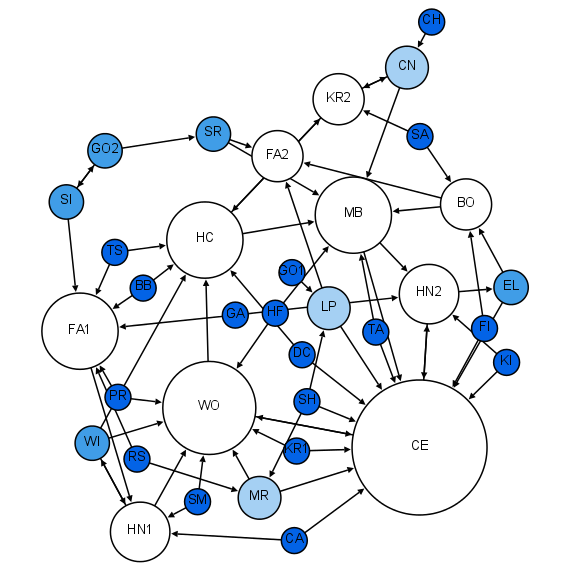
Network Science
Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by ''nodes'' (or ''vertices'') and the connections between the elements or actors as ''links'' (or ''edges''). The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena." Background and history The study of networks has emerged in diverse disciplines as a means of analyzing complex relational data. The earliest known paper in this f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tree (graph Theory)
In graph theory In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are conne ..., a tree is an undirected graph in which any two Vertex (graph theory), vertices are connected by ''exactly one'' Path (graph theory), path, or equivalently a Connected graph, connected Cycle (graph theory), acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by ''at most one'' path, or equivalently an acyclic undirected graph, or equivalently a Disjoint union of graphs, disjoint union of trees. A polytreeSee . (or directed tree or oriented treeSee .See . or singly connected networkSee .) is a directed acyclic graph (DAG) whose underlying undirected graph is a tree. A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirecte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |