|
Pentagramma Mirificum
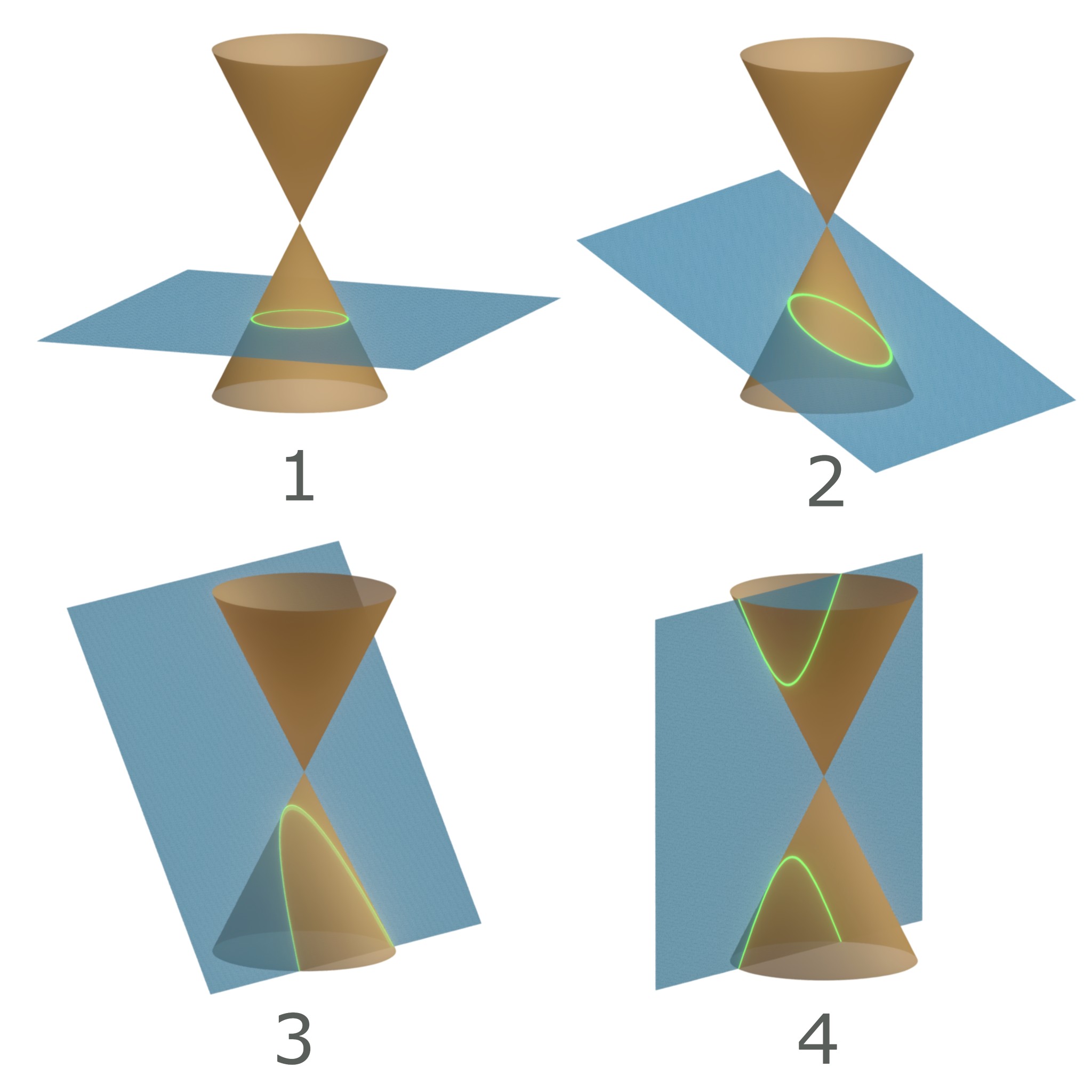
Pentagramma mirificum (Latin for ''miraculous pentagram'') is a star polygon on a sphere, composed of five great circle arcs, all of whose internal angles are right angles. This shape was described by John Napier in his 1614 book ''Mirifici Logarithmorum Canonis Descriptio'' (''Description of the Admirable Table of Logarithms'') along with rules that link the values of trigonometric functions of five parts of a right spherical triangle (two angles and three sides). The properties of ''pentagramma mirificum'' were studied, among others, by Carl Friedrich Gauss. Geometric properties On a sphere, both the angles and the sides of a triangle (arcs of great circles) are measured as angles. There are five right angles, each measuring \pi/2, at A, B, C, D, and E. There are ten arcs, each measuring \pi/2: PC, PE, QD, QA, RE, RB, SA, SC, TB, and TD. In the spherical pentagon PQRST, every vertex is the pole of the opposite side. For instance, point P is the pole of equator RS, point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Triangle
A right triangle (American English) or right-angled triangle (British), or more formally an orthogonal triangle, formerly called a rectangled triangle ( grc, ὀρθόσγωνία, lit=upright angle), is a triangle in which one angle is a right angle (that is, a 90-degree angle), i.e., in which two sides are perpendicular. The relation between the sides and other angles of the right triangle is the basis for trigonometry. The side opposite to the right angle is called the ''hypotenuse'' (side ''c'' in the figure). The sides adjacent to the right angle are called ''legs'' (or ''catheti'', singular: ''cathetus''). Side ''a'' may be identified as the side ''adjacent to angle B'' and ''opposed to'' (or ''opposite'') ''angle A'', while side ''b'' is the side ''adjacent to angle A'' and ''opposed to angle B''. If the lengths of all three sides of a right triangle are integers, the triangle is said to be a Pythagorean triangle and its side lengths are collectively known as a ''Pythagor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a prolific United Kingdom of Great Britain and Ireland, British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics. As a child, Cayley enjoyed solving complex maths problems for amusement. He entered Trinity College, Cambridge, where he excelled in Greek language, Greek, French language, French, German language, German, and Italian language, Italian, as well as mathematics. He worked as a lawyer for 14 years. He postulated the Cayley–Hamilton theorem—that every square matrix is a root of its own characteristic polynomial, and verified it for matrices of order 2 and 3. He was the first to define the concept of a group (mathematics), group in the modern way—as a set with a Binary function, binary operation satisfying certain laws. Formerly, when mathematicians spoke of "groups", they had meant permutation groups. Cayley tables and Cayley graphs as well as Cayle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytic geometry, Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Five Points Determine A Conic
In Euclidean and projective geometry, just as two (distinct) points determine a line (a degree-1 plane curve), five points determine a conic (a degree-2 plane curve). There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines. Formally, given any five points in the plane in general linear position, meaning no three collinear, there is a unique conic passing through them, which will be non-degenerate; this is true over both the Euclidean plane and any pappian projective plane. Indeed, given any five points there is a conic passing through them, but if three of the points are collinear the conic will be degenerate (reducible, because it contains a line), and may not be unique; see further discussion. Proofs This result can be proven numerous different ways; the dimension counting argument is most direct, and generalizes to higher degree, while other proofs are special to conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
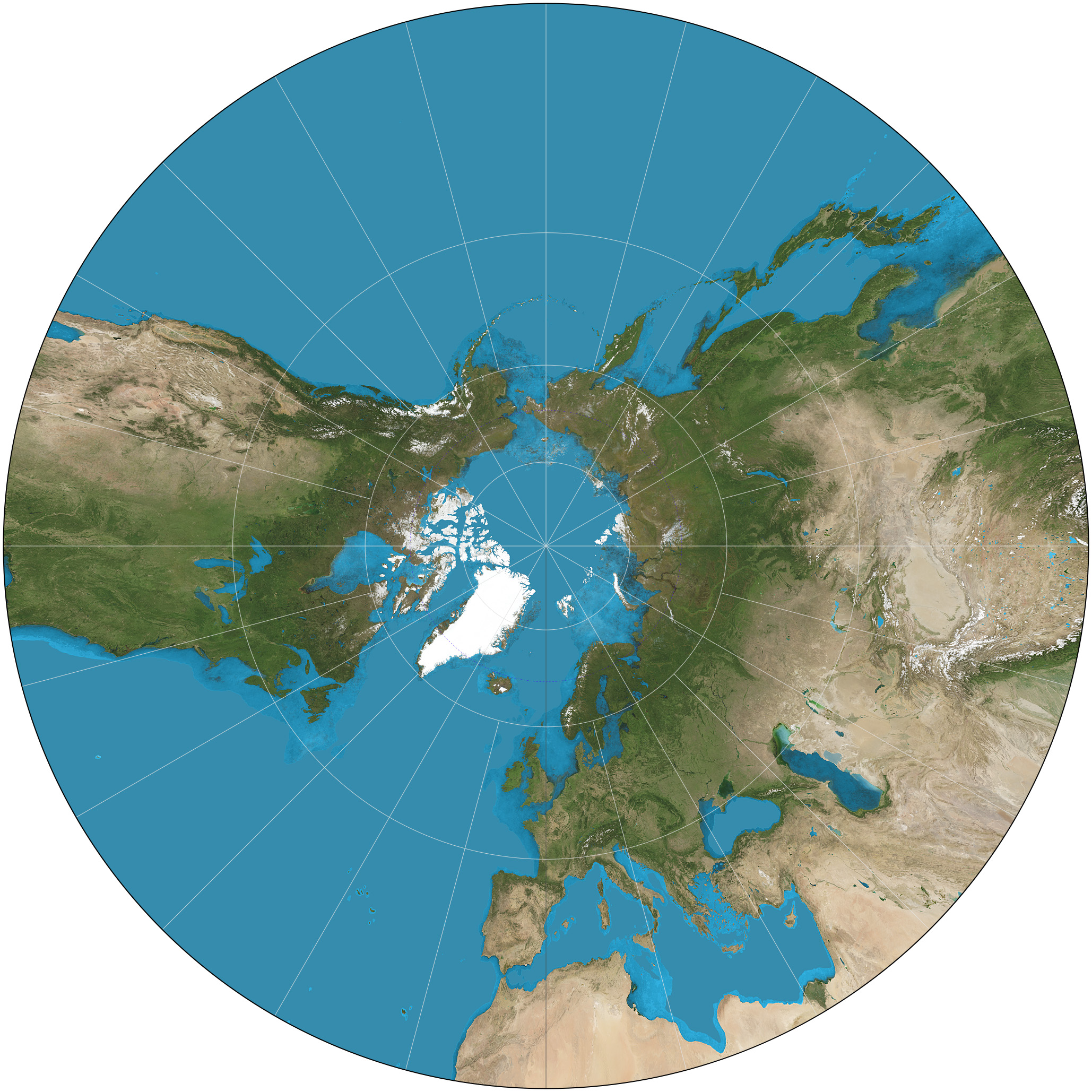
Gnomonic Projection
A gnomonic map projection is a map projection which displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. This is achieved by casting surface points of the sphere onto a tangent plane, each landing where a ray from the center of the sphere passes through the point on the surface and then on to the plane. No distortion occurs at the tangent point, but distortion increases rapidly away from it. Less than half of the sphere can be projected onto a finite map. Consequently, a rectilinear photographic lens, which is based on the gnomonic principle, cannot image more than 180 degrees. History The gnomonic projection is said to be the oldest map projection, developed by Thales for star maps in the 6th century BC. The path of the shadow-tip or light-spot in a nodus-based sundial traces out the same hyperbolae formed by parallels on a gnomonic map. Properties Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional object has an infinite number of possible central axes and rotational directions. If the rotation axis passes internally through the body's own center of mass, then the body is said to be ''autorotating'' or '' spinning'', and the surface intersection of the axis can be called a ''pole''. A rotation around a completely external axis, e.g. the planet Earth around the Sun, is called ''revolving'' or ''orbiting'', typically when it is produced by gravity, and the ends of the rotation axis can be called the ''orbital poles''. Mathematics Mathematically, a rotation is a rigid body movement which, unlike a translation, keeps a point fixed. This definition applies to rotations within both two and three dimensions (in a plane and in space, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook ''Spherical trigonometry for the use of colleges and Schools''. Since then, significant developments have been the application of vector methods, quaternion methods, and the use of numerical methods. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes referred to as the ''Princeps mathematicorum'' () and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and he is ranked among history's most influential mathematicians. Also available at Retrieved 23 February 2014. Comprehensive biographical article. Biography Early years Johann Carl Friedrich Gauss was born on 30 April 1777 in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany), to poor, working-class parents. His mother was illiterate and never recorded the date of his birth, remembering only that he had been born on a Wednesday, eight days before the Feast of the Ascension (which occurs 39 days after Easter). Ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star Polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple and star polygons. Branko Grünbaum identified two primary definitions used by Johannes Kepler, one being the regular star polygons with intersecting edges that don't generate new vertices, and the second being simple isotoxal concave polygons. The first usage is included in polygrams which includes polygons like the pentagram but also compound figures like the hexagram. One definition of a ''star polygon'', used in turtle graphics, is a polygon having 2 or more turns (turning number and density), like in spirolaterals.Abelson, Harold, diSessa, Andera, 1980, ''Turtle Geometry'', MIT Press, p.24 Etymology Star polygon names combine a numeral prefix, such as ''penta-'', with the Greek suffix '' -gram'' (in this cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |