|
Patched Conics
In astrodynamics, the patched conic approximation or patched two-body approximation is a method to simplify trajectory calculations for spacecraft in a multiple-body environment. Method The simplification is achieved by dividing space into various parts by assigning each of the ''n'' bodies (e.g. the Sun, planets, moons) its own sphere of influence (astrodynamics), sphere of influence. When the spacecraft is within the sphere of influence of a smaller body, only the gravitational force between the spacecraft and that smaller body is considered, otherwise the gravitational force between the spacecraft and the larger body is used. This reduces a complicated n-body problem to multiple two-body problems, for which the solutions are the well-known conic sections of the Kepler orbits. Although this method gives a good approximation of trajectories for interplanetary spaceflight, interplanetary spacecraft missions, there are missions for which this approximation does not provide suffici ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and the Newton's law of universal gravitation, law of universal gravitation. Orbital mechanics is a core discipline within space exploration, space-mission design and control. Celestial mechanics treats more broadly the orbital dynamics of systems under the influence of gravity, including both spacecraft and natural astronomical object, astronomical bodies such as star systems, planets, Natural satellite, moons, and comets. Orbital mechanics focuses on spacecraft trajectory, trajectories, including orbital maneuvers, orbital plane (astronomy), orbital plane changes, and interplanetary transfers, and is used by mission planners to predict the results of spacecraft propulsion, propulsive maneuvers. General relativity is a more exact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Point
In celestial mechanics, the Lagrange points (; also Lagrangian points or libration points) are points of equilibrium for small-mass objects under the influence of two massive orbiting bodies. Mathematically, this involves the solution of the restricted three-body problem in which two bodies are far more massive than the third. Normally, the two massive bodies exert an unbalanced gravitational force at a point, altering the orbit of whatever is at that point. At the Lagrange points, the gravitational forces of the two large bodies and the centrifugal force balance each other. This can make Lagrange points an excellent location for satellites, as few orbit corrections are needed to maintain the desired orbit. Small objects placed in orbit at Lagrange points are in equilibrium in at least two directions relative to the center of mass of the large bodies. For any combination of two orbital bodies there are five Lagrange points, L1 to L5, all in the orbital plane of the two lar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere Of Influence (astrodynamics)
A sphere of influence (SOI) in astrodynamics and astronomy is the oblate spheroid, oblate-spheroid-shaped region around a celestial body where the primary gravity, gravitational influence on an orbiting object is that body. This is usually used to describe the areas in the Solar System where planets dominate the orbits of surrounding objects such as natural satellite, moons, despite the presence of the much more massive but distant Sun. In the patched conic approximation, used in estimating the trajectories of bodies moving between the neighbourhoods of different masses using a two body approximation, ellipses and hyperbolae, the SOI is taken as the boundary where the trajectory switches which mass field it is influenced by. The general equation describing the radius of the sphere r_ of a planet: : r_ \approx a\left(\frac\right)^ where : a is the semimajor axis of the smaller object's (usually a planet's) orbit around the larger body (usually the Sun). : m and M are the masses of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-body Problem
In physics, the -body problem is the problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally.Leimanis and Minorsky: Our interest is with Leimanis, who first discusses some history about the -body problem, especially Ms. Kovalevskaya's 1868–1888 twenty-year complex-variables approach, failure; Section 1: "The Dynamics of Rigid Bodies and Mathematical Exterior Ballistics" (Chapter 1, "The motion of a rigid body about a fixed point (Euler and Poisson equations)"; Chapter 2, "Mathematical Exterior Ballistics"), good precursor background to the -body problem; Section 2: "Celestial Mechanics" (Chapter 1, "The Uniformization of the Three-body Problem (Restricted Three-body Problem)"; Chapter 2, "Capture in the Three-Body Problem"; Chapter 3, "Generalized -body Problem"). Solving this problem has been motivated by the desire to understand the motions of the Sun, Moon, planets, and visible stars. In the 20th century, unde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-body Problem
In classical mechanics, the two-body problem is to predict the motion of two massive objects which are abstractly viewed as point particles. The problem assumes that the two objects interact only with one another; the only force affecting each object arises from the other one, and all other objects are ignored. The most prominent case of the classical two-body problem is the gravitational case (see also Kepler problem), arising in astronomy for predicting the orbits (or escapes from orbit) of objects such as satellites, planets, and stars. A two-point-particle model of such a system nearly always describes its behavior well enough to provide useful insights and predictions. A simpler "one body" model, the " central-force problem", treats one object as the immobile source of a force acting on the other. One then seeks to predict the motion of the single remaining mobile object. Such an approximation can give useful results when one object is much more massive than the other (as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
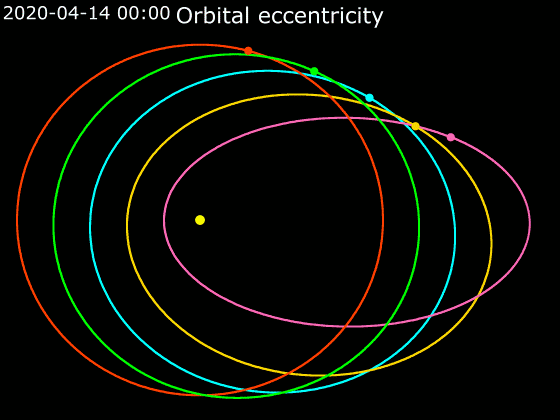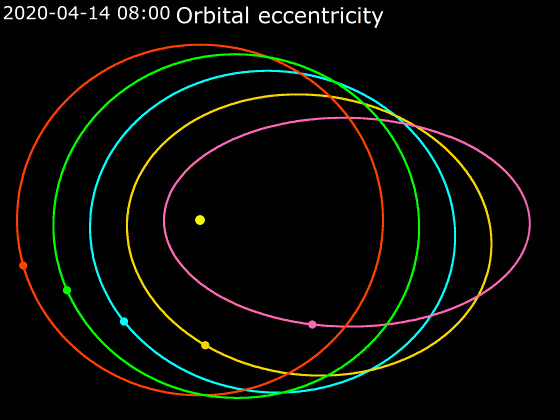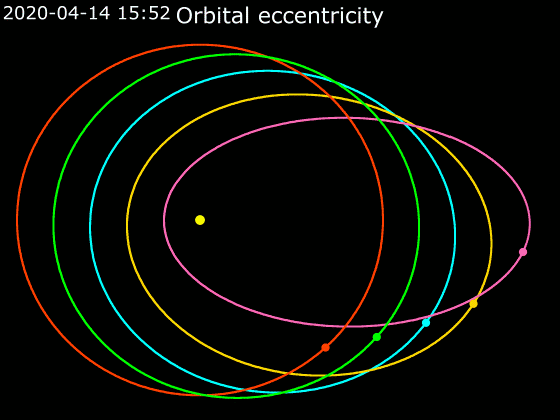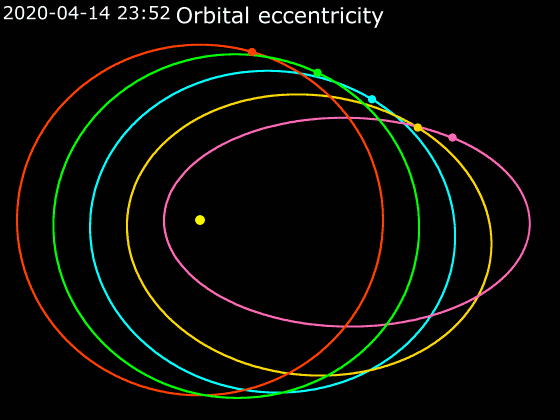
Elliptic Orbit
In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 (thus excluding the circular orbit). In a wider sense, it is a Kepler's orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1. In a gravitational two-body problem with negative energy, both bodies follow similar elliptic orbits with the same orbital period around their common barycenter. Also the relative position of one body with respect to the other follows an elliptic orbit. Examples of elliptic orbits include: Hohmann transfer orbit, Molniya orbit, and tundra orbit. Velocity Under standard assumptions, no other forces acting except two spherically symmetrical bodies m1 and m2, the orbital speed (v\,) of one body trave ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravity Well
The Hill sphere of an astronomical body is the region in which it dominates the attraction of satellites. To be retained by a planet, a moon must have an orbit that lies within the planet's Hill sphere. That moon would, in turn, have a Hill sphere of its own. Any object within that distance would tend to become a satellite of the moon, rather than of the planet itself. One simple view of the extent of the Solar System is the Hill sphere of the Sun with respect to local stars and the galactic nucleus. In more precise terms, the Hill sphere approximates the gravitational sphere of influence of a smaller body in the face of perturbations from a more massive body. It was defined by the American astronomer George William Hill, based on the work of the French astronomer Édouard Roche. In the example to the right, the Earth's Hill sphere extends between the Lagrange points and , which lie along the line of centers of the two bodies. The region of influence of the smaller body is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Trajectory
In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one. Under simplistic assumptions a body traveling along this trajectory will coast towards infinity, settling to a final excess velocity relative to the central body. Similarly to parabolic trajectories, all hyperbolic trajectories are also escape trajectories. The specific energy of a hyperbolic trajectory orbit is positive. Planetary flybys, used for gravitational slingshots, can be described within the planet's sphere of influence using hyperbolic trajectories. Parameters describing a hyperbolic trajectory Like an elliptical orbit, a hyperbol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mars
Mars is the fourth planet from the Sun and the second-smallest planet in the Solar System, only being larger than Mercury (planet), Mercury. In the English language, Mars is named for the Mars (mythology), Roman god of war. Mars is a terrestrial planet with a thin atmosphere (less than 1% that of Earth's), and has a crust primarily composed of elements similar to Earth's crust, as well as a core made of iron and nickel. Mars has surface features such as impact craters, valleys, dunes and polar ice caps. It has two small and irregularly shaped moons, Phobos (moon), Phobos and Deimos (moon), Deimos. Some of the most notable surface features on Mars include Olympus Mons, the largest volcano and List of tallest mountains in the Solar System, highest known mountain in the Solar System and Valles Marineris, one of the largest canyons in the Solar System. The North Polar Basin (Mars), Borealis basin in the Northern Hemisphere covers approximately 40% of the planet and may be a la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surface is made up of the ocean, dwarfing Earth's polar ice, lakes, and rivers. The remaining 29% of Earth's surface is land, consisting of continents and islands. Earth's surface layer is formed of several slowly moving tectonic plates, which interact to produce mountain ranges, volcanoes, and earthquakes. Earth's liquid outer core generates the magnetic field that shapes the magnetosphere of the Earth, deflecting destructive solar winds. The atmosphere of the Earth consists mostly of nitrogen and oxygen. Greenhouse gases in the atmosphere like carbon dioxide (CO2) trap a part of the energy from the Sun close to the surface. Water vapor is widely present in the atmosphere and forms clouds that cover most of the planet. More solar e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interplanetary Spaceflight
Interplanetary spaceflight or interplanetary travel is the crewed or uncrewed travel between stars and planets, usually within a single planetary system. In practice, spaceflights of this type are confined to travel between the planets of the Solar System. Uncrewed space probes have flown to all the observed planets in the Solar System as well as to dwarf planets Pluto and Ceres, and several asteroids. Orbiters and landers return more information than fly-by missions. Crewed flights have landed on the Moon and have been planned, from time to time, for Mars, Venus and Mercury. While many scientists appreciate the knowledge value that uncrewed flights provide, the value of crewed missions is more controversial. Science fiction writers propose a number of benefits, including the mining of asteroids, access to solar power, and room for colonization in the event of an Earth catastrophe. A number of techniques have been developed to make interplanetary flights more economical. Advanc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trajectory
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete trajectory is defined by position and momentum, simultaneously. The mass might be a projectile or a satellite. For example, it can be an orbit — the path of a planet, asteroid, or comet as it travels around a central mass. In control theory, a trajectory is a time-ordered set of states of a dynamical system (see e.g. Poincaré map). In discrete mathematics, a trajectory is a sequence (f^k(x))_ of values calculated by the iterated application of a mapping f to an element x of its source. Physics of trajectories A familiar example of a trajectory is the path of a projectile, such as a thrown ball or rock. In a significantly simplified model, the object moves only under the influence of a uniform gravitational force field. This can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |