|
Purity (quantum Mechanics)
In quantum mechanics, and especially quantum information theory, the purity of a normalized quantum state is a scalar defined as \gamma \, \equiv \, \operatorname(\rho^2) where \rho \, is the density matrix of the state and \operatorname is the trace operation. The purity defines a measure on quantum states, giving information on how much a state is mixed. Mathematical properties The purity of a normalized quantum state satisfies \frac1d \leq \gamma \leq 1 \,, where d is the dimension of the Hilbert space upon which the state is defined. The upper bound is obtained by \operatorname(\rho) = 1 \,and \operatorname(\rho^2) \leq \operatorname(\rho) \,(see trace). If \rho \, is a projection, which defines a pure state, then the upper bound is saturated: \operatorname(\rho^2)= \operatorname(\rho)=1 \, (see Projections). The lower bound is obtained by the completely mixed state, represented by the matrix \frac1d I_d \,. The purity of a quantum state is conserved under unitary tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diagonalizable Matrix
In linear algebra, a square matrix A is called diagonalizable or non-defective if it is matrix similarity, similar to a diagonal matrix. That is, if there exists an invertible matrix P and a diagonal matrix D such that . This is equivalent to (Such D are not unique.) This property exists for any linear map: for a dimension (vector space), finite-dimensional vector space a linear map T:V\to V is called diagonalizable if there exists an Basis (linear algebra)#Ordered bases and coordinates, ordered basis of V consisting of eigenvectors of T. These definitions are equivalent: if T has a matrix (mathematics), matrix representation A = PDP^ as above, then the column vectors of P form a basis consisting of eigenvectors of and the diagonal entries of D are the corresponding eigenvalues of with respect to this eigenvector basis, T is represented by Diagonalization is the process of finding the above P and and makes many subsequent computations easier. One can raise a diag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metal
A metal () is a material that, when polished or fractured, shows a lustrous appearance, and conducts electrical resistivity and conductivity, electricity and thermal conductivity, heat relatively well. These properties are all associated with having electrons available at the Fermi level, as against nonmetallic materials which do not. Metals are typically ductile (can be drawn into a wire) and malleable (can be shaped via hammering or pressing). A metal may be a chemical element such as iron; an alloy such as stainless steel; or a molecular compound such as polythiazyl, polymeric sulfur nitride. The general science of metals is called metallurgy, a subtopic of materials science; aspects of the electronic and thermal properties are also within the scope of condensed matter physics and solid-state chemistry, it is a multidisciplinary topic. In colloquial use materials such as steel alloys are referred to as metals, while others such as polymers, wood or ceramics are nonmetallic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Insulator (electricity)
An electrical insulator is a material in which electric current does not flow freely. The atoms of the insulator have tightly bound electrons which cannot readily move. Other materials—semiconductors and electrical conductor, conductors—conduct electric current more easily. The property that distinguishes an insulator is its resistivity; insulators have higher resistivity than semiconductors or conductors. The most common examples are Nonmetal (chemistry), non-metals. A perfect insulator does not exist because even the materials used as insulators contain small numbers of mobile charges (charge carriers) which can carry current. In addition, all insulators become electrically conductive when a sufficiently large voltage is applied that the electric field tears electrons away from the atoms. This is known as electrical breakdown, and the voltage at which it occurs is called the breakdown voltage of an insulator. Some materials such as glass, Electrical insulation paper, paper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condensed Matter Physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid State of matter, phases, that arise from electromagnetic forces between atoms and electrons. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconductivity, superconducting phase exhibited by certain materials at extremely low cryogenic temperatures, the ferromagnetic and antiferromagnetic phases of Spin (physics), spins on crystal lattices of atoms, the Bose–Einstein condensates found in ultracold atomic systems, and liquid crystals. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theoretical physics, physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter), psi, respectively). Wave functions are complex number, complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density function, probability density of measurement in quantum mechanics, measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called ''normalization''. Since the wave function is complex-valued, only its relative phase and relative magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position And Momentum Space
In physics and geometry, there are two closely related vector spaces, usually three-dimensional but in general of any finite dimension. Position space (also real space or coordinate space) is the set of all ''position vectors'' r in Euclidean space, and has dimensions of length; a position vector defines a point in space. (If the position vector of a point particle varies with time, it will trace out a path, the trajectory of a particle.) Momentum space is the set of all ''momentum vectors'' p a physical system can have; the momentum vector of a particle corresponds to its motion, with dimension of masslengthtime−1. Mathematically, the duality between position and momentum is an example of ''Pontryagin duality''. In particular, if a function is given in position space, ''f''(r), then its Fourier transform obtains the function in momentum space, ''φ''(p). Conversely, the inverse Fourier transform of a momentum space function is a position space function. These quantities and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
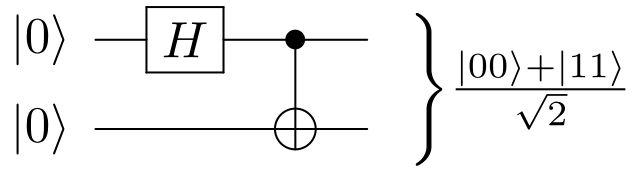
Bell State
In quantum information science, the Bell's states or EPR pairs are specific quantum states of two qubits that represent the simplest examples of quantum entanglement. The Bell's states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particles being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will " collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell's state the two qubits are in initially. Bell's states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for three or more subsystems. Understanding of Bell's states is useful in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negativity (quantum Mechanics)
In quantum mechanics, negativity is a measure of quantum entanglement which is easy to compute. It is a measure deriving from the PPT criterion for separability. It has been shown to be an entanglement monotone and hence a proper measure of entanglement. Definition The negativity of a subsystem A can be defined in terms of a density matrix \rho as: :\mathcal(\rho) \equiv \frac where: * \rho^ is the partial transpose of \rho with respect to subsystem A * , , X, , _1 = \text, X, = \text \sqrt is the trace norm or the sum of the singular values of the operator X . An alternative and equivalent definition is the absolute sum of the negative eigenvalues of \rho^: : \mathcal(\rho) = \left, \sum_ \lambda_i \ = \sum_i \frac where \lambda_i are all of the eigenvalues. Properties * Is a convex function of \rho: :\mathcal(\sum_p_\rho_) \le \sum_p_\mathcal(\rho_) * Is an entanglement monotone: :\mathcal(P(\rho)) \le \mathcal(\rho) where P(\rho) is an arbitrary LOCC LOCC ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Transpose
Partial may refer to: Mathematics *Partial derivative, derivative with respect to one of several variables of a function, with the other variables held constant ** ∂, a symbol that can denote a partial derivative, sometimes pronounced "partial dee" **Partial differential equation, a differential equation that contains unknown multivariable functions and their partial derivatives Other uses *Partial application, in computer science the process of fixing a number of arguments to a function, producing another function *Partial charge or net atomic charge, in chemistry a charge value that is not an integer or whole number *Partial fingerprint, impression of human fingers used in criminology or forensic science *Partial seizure or focal seizure, a seizure that initially affects only one hemisphere of the brain * Partial or Part score, in contract bridge a trick score less than 100, as well as other meanings * Partial or Partial wave, one sound wave of which a complex tone is composed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peres–Horodecki Criterion
The Peres–Horodecki criterion is a necessary condition, for the joint density matrix \rho of two quantum mechanical systems A and B, to be separable. It is also called the PPT criterion, for ''positive partial transpose''. In the 2×2 and 2×3 dimensional cases the condition is also sufficient. It is used to decide the separability of mixed states, where the Schmidt decomposition does not apply. The theorem was discovered in 1996 by Asher Peres and the Horodecki family ( Michał, Paweł, and Ryszard) In higher dimensions, the test is inconclusive, and one should supplement it with more advanced tests, such as those based on entanglement witnesses. Definition If we have a general state \rho which acts on Hilbert space of \mathcal_A \otimes \mathcal_B :\rho = \sum_ p^_ , i\rangle \langle j , \otimes , k\rangle \langle l, Its partial transpose (with respect to the B party) is defined as :\rho^ := (I \otimes T) (\rho) = \sum_ p^ _ , i\rangle \langle j , \otimes (, k\ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |