|
Proof Net
In proof theory, proof nets are a geometrical method of representing proofs that eliminates two forms of ''bureaucracy'' that differentiate proofs: (A) irrelevant syntactical features of regular proof calculi, and (B) the order of rules applied in a derivation. In this way, the formal properties of proof identity correspond more closely to the intuitively desirable properties. Proof nets were introduced by Jean-Yves Girard. This distinguishes proof nets from regular proof calculi such as the natural deduction calculus and the sequent calculus, where these phenomena are present. For instance, these two linear logic proofs are identical: And their corresponding nets will be the same. Correctness criteria Several correctness criteria are known to check if a sequential proof structure (i.e. something which seems to be a proof net) is actually a concrete proof structure (i.e. something which encodes a valid derivation in linear logic). The first such criterion is the long-tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proof Theory
Proof theory is a major branchAccording to Wang (1981), pp. 3–4, proof theory is one of four domains mathematical logic, together with model theory, axiomatic set theory, and recursion theory. Barwise (1978) consists of four corresponding parts, with part D being about "Proof Theory and Constructive Mathematics". of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as lists, boxed lists, or trees, which are constructed according to the axioms and rules of inference of the logical system. Consequently, proof theory is syntactic in nature, in contrast to model theory, which is semantic in nature. Some of the major areas of proof theory include structural proof theory, ordinal analysis, provability logic, reverse mathematics, proof mining, automated theorem proving, and proof complexity. Much research also focuses ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean-Yves Girard
Jean-Yves Girard (; born 1947) is a French logician working in proof theory. He is the research director (emeritus) at the mathematical institute of the University of Aix-Marseille, at Luminy. Biography Jean-Yves Girard is an alumnus of the École normale supérieure de Saint-Cloud. He made a name for himself in the 1970s with his proof of strong normalization in a system of second-order logic called System F. This result gave a new proof of Takeuti's conjecture, which was proven a few years earlier by William W. Tait, Motō Takahashi and Dag Prawitz. For this purpose, he introduced the notion of "reducibility candidate" ("candidat de réducibilité"). He is also credited with the discovery of Girard's paradox, linear logic, the geometry of interaction, ludics, and (satirically) the mustard watch. He obtained the CNRS Silver medal in 1983 and is a member of the French Academy of Sciences The French Academy of Sciences (French: ''Académie des sciences'') is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning. This contrasts with Hilbert-style systems, which instead use axioms as much as possible to express the logical laws of deductive reasoning. Motivation Natural deduction grew out of a context of dissatisfaction with the axiomatizations of deductive reasoning common to the systems of Hilbert, Frege, and Russell (see, e.g., Hilbert system). Such axiomatizations were most famously used by Russell and Whitehead in their mathematical treatise '' Principia Mathematica''. Spurred on by a series of seminars in Poland in 1926 by Łukasiewicz that advocated a more natural treatment of logic, Jaśkowski made the earliest attempts at defining a more natural deduction, first in 1929 using a diagrammatic notation, and later updating his proposal in a sequence of papers in 1934 and 1935. His proposals led to d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequent Calculus
In mathematical logic, sequent calculus is a style of formal logical argumentation in which every line of a proof is a conditional tautology (called a sequent by Gerhard Gentzen) instead of an unconditional tautology. Each conditional tautology is inferred from other conditional tautologies on earlier lines in a formal argument according to rules and procedures of inference, giving a better approximation to the natural style of deduction used by mathematicians than to David Hilbert's earlier style of formal logic, in which every line was an unconditional tautology. More subtle distinctions may exist; for example, propositions may implicitly depend upon non-logical axioms. In that case, sequents signify conditional theorems in a first-order language rather than conditional tautologies. Sequent calculus is one of several extant styles of proof calculus for expressing line-by-line logical arguments. * Hilbert style. Every line is an unconditional tautology (or theorem). * Gentze ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter. Although the logic has also been studied for its own sake, more broadly, ideas from linear logic have been influential in fields such as programming languages, game semantics, and quantum physics (because linear logic can be seen as the logic of quantum information theory), as well as linguistics, particularly because of its emphasis on resource-boundedness, duality, and interaction. Linear logic lends itself to many different presentations, explanations, and intuitions. Proof-theoretically, it derives from an analysis of classical sequent calculus in which uses of (the structural rules) contraction and weakening are carefully controlled. Operationally, this means that logical deduction is no longer merely about an ever-expanding collection of persistent "truth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter. Although the logic has also been studied for its own sake, more broadly, ideas from linear logic have been influential in fields such as programming languages, game semantics, and quantum physics (because linear logic can be seen as the logic of quantum information theory), as well as linguistics, particularly because of its emphasis on resource-boundedness, duality, and interaction. Linear logic lends itself to many different presentations, explanations, and intuitions. Proof-theoretically, it derives from an analysis of classical sequent calculus in which uses of (the structural rules) contraction and weakening are carefully controlled. Operationally, this means that logical deduction is no longer merely about an ever-expanding collection of persistent "truth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ludics
In proof theory, ludics is an analysis of the principles governing inference rules of mathematical logic. Key features of ludics include notion of compound connectives, using a technique known as ''focusing'' or ''focalisation'' (invented by the computer scientist Jean-Marc Andreoli), and its use of ''locations'' or ''loci'' over a base instead of propositions. More precisely, ludics tries to retrieve known logical connectives and proof behaviours by following the paradigm of interactive computation, similarly to what is done in game semantics to which it is closely related. By abstracting the notion of formulae and focusing on their concrete uses—that is distinct occurrences—it provides an abstract syntax for computer science, as loci can be seen as pointers on memory. The primary achievement of ludics is the discovery of a relationship between two natural, but distinct notions of type, or proposition. The first view, which might be termed the proof-theoretic or Gentzen-sty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coherent Space
In proof theory, a coherent space (also coherence space) is a concept introduced in the semantic study of linear logic. Let a set ''C'' be given. Two subsets ''S'',''T'' ⊆ ''C'' are said to be ''orthogonal'', written ''S'' ⊥ ''T'', if ''S'' ∩ ''T'' is ∅ or a singleton. The ''dual'' of a family ''F'' ⊆ ℘(''C'') is the family ''F'' ⊥ of all subsets ''S'' ⊆ ''C'' orthogonal to every member of ''F'', i.e., such that ''S'' ⊥ ''T'' for all ''T'' ∈ ''F''. A coherent space ''F'' over ''C'' is a family of ''C''-subsets for which ''F'' = (''F'' ⊥) ⊥. In ''Proofs and Types'' coherent spaces are called coherence spaces. A footnote explains that although in the French original they were ''espaces cohérents'', the coherence space translation was used because spectral spaces are sometimes called coherent spaces. Definitions As defined by Jean-Yves Girard, a ''coherence space'' \mathcal is a collection of sets satisfying down-closure and binary completeness in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deep Inference
Deep inference names a general idea in structural proof theory that breaks with the classical sequent calculus by generalising the notion of structure to permit inference to occur in contexts of high structural complexity. The term ''deep inference'' is generally reserved for proof calculi where the structural complexity is unbounded; in this article we will use non-shallow inference to refer to calculi that have structural complexity greater than the sequent calculus, but not unboundedly so, although this is not at present established terminology. Deep inference is not important in logic outside of structural proof theory, since the phenomena that lead to the proposal of formal systems with deep inference are all related to the cut-elimination theorem. The first calculus of deep inference was proposed by Kurt Schütte,Kurt Schütte. Proof Theory. Springer-Verlag, 1977. but the idea did not generate much interest at the time. Nuel Belnap proposed display logic in an attem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
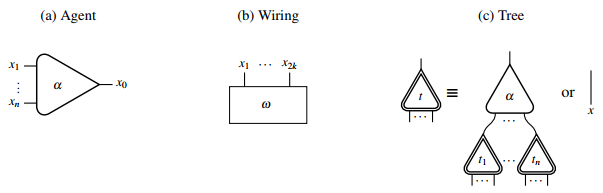
Interaction Nets
Interaction nets are a graphical model of computation devised by Yves Lafont in 1990 as a generalisation of the proof structures of linear logic. An interaction net system is specified by a set of agent types and a set of interaction rules. Interaction nets are an inherently distributed model of computation in the sense that computations can take place simultaneously in many parts of an interaction net, and no synchronisation is needed. The latter is guaranteed by the strong confluence property of reduction in this model of computation. Thus interaction nets provide a natural language for massive parallelism. Interaction nets are at the heart of many implementations of the lambda calculus, such as efficient closed reduction and optimal, in Lévy's sense, Lambdascope. Definitions Interactions nets are graph-like structures consisting of ''agents'' and ''edges''. An agent of type \alpha and with ''arity'' \text(\alpha) = n \ge 0 has one ''principal port'' and n ''auxiliary ports'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |