|
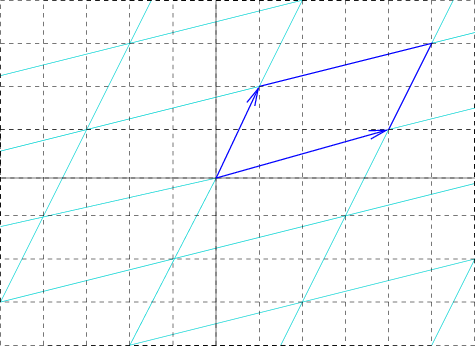
Primitive Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations. There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2d Op Rectangular
D, or d, is the fourth letter in the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''dee'' (pronounced ), plural ''dees''. History The Semitic letter Dāleth may have developed from the logogram for a fish or a door. There are many different Egyptian hieroglyphs that might have inspired this. In Semitic, Ancient Greek and Latin, the letter represented ; in the Etruscan alphabet the letter was archaic, but still retained (see letter B). The equivalent Greek letter is Delta, Δ. Architecture The minuscule (lower-case) form of 'd' consists of a lower-story left bowl and a stem ascender. It most likely developed by gradual variations on the majuscule (capital) form 'D', and today now composed as a stem with a full lobe to the right. In handwriting, it was common to start the arc to the left of the vertical stroke, resulting in a serif at the top of the arc. This serif w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetragonal
In crystallography, the tetragonal crystal system is one of the 7 crystal systems. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base (''a'' by ''a'') and height (''c'', which is different from ''a''). Bravais lattices There are two tetragonal Bravais lattices: the primitive tetragonal and the body-centered tetragonal. The base-centered tetragonal lattice is equivalent to the primitive tetragonal lattice with a smaller unit cell, while the face-centered tetragonal lattice is equivalent to the body-centered tetragonal lattice with a smaller unit cell. Crystal classes The point groups that fall under this crystal system are listed below, followed by their representations in international notation, Schoenflies notation, orbifold notation, Coxeter notation and mineral examples.Hurlbut, Cornelius S.; Klein, Cornelis, 1985, ''Manual of Mineralogy'', 20th ed., p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthorhombic
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (''a'' by ''b'') and height (''c''), such that ''a'', ''b'', and ''c'' are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal. Bravais lattices There are four orthorhombic Bravais lattices: primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic. For the base-centered orthorhombic lattice, the primitive cell has the shape of a right rhombic prism;See , row oC, column Primitive, where the cell parameters are given as a1 = a2, α = β = 90° it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. Note that the length a of the primit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monoclinic
In crystallography, the monoclinic crystal system is one of the seven crystal systems. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a parallelogram prism. Hence two pairs of vectors are perpendicular (meet at right angles), while the third pair makes an angle other than 90°. Bravais lattices Two monoclinic Bravais lattices exist: the primitive monoclinic and the base-centered monoclinic. For the base-centered monoclinic lattice, the primitive cell has the shape of an oblique rhombic prism;See , row mC, column Primitive, where the cell parameters are given as a1 = a2, α = β it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. Note that the length a of the primitive cell below equals \frac \sqrt of the conventional cell above. Crystal classes The table below org ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triclinic
180px, Triclinic (a ≠ b ≠ c and α ≠ β ≠ γ ) In crystallography, the triclinic (or anorthic) crystal system is one of the 7 crystal systems. A crystal system is described by three basis vectors. In the triclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system. In addition, the angles between these vectors must all be different and may not include 90°. The triclinic lattice is the least symmetric of the 14 three-dimensional Bravais lattices. It has (itself) the minimum symmetry all lattices have: points of inversion at each lattice point and at 7 more points for each lattice point: at the midpoints of the edges and the faces, and at the center points. It is the only lattice type that itself has no mirror planes. Crystal classes The triclinic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation, point groups, International Tables for Crystallography space group number, orbifold, type, and sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelepiped 2013-11-29
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, the four concepts—''parallelepiped'' and ''cube'' in three dimensions, ''parallelogram'' and ''square'' in two dimensions—are defined, but in the context of a more general affine geometry, in which angles are not differentiated, only ''parallelograms'' and ''parallelepipeds'' exist. Three equivalent definitions of ''parallelepiped'' are *a polyhedron with six faces (hexahedron), each of which is a parallelogram, *a hexahedron with three pairs of parallel faces, and *a prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all specific cases of parallelepiped. "Parallelepiped" is now usually pronounced or ; trad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2d Oc Rectangular
D, or d, is the fourth letter in the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''dee'' (pronounced ), plural ''dees''. History The Semitic letter Dāleth may have developed from the logogram for a fish or a door. There are many different Egyptian hieroglyphs that might have inspired this. In Semitic, Ancient Greek and Latin, the letter represented ; in the Etruscan alphabet the letter was archaic, but still retained (see letter B). The equivalent Greek letter is Delta, Δ. Architecture The minuscule (lower-case) form of 'd' consists of a lower-story left bowl and a stem ascender. It most likely developed by gradual variations on the majuscule (capital) form 'D', and today now composed as a stem with a full lobe to the right. In handwriting, it was common to start the arc to the left of the vertical stroke, resulting in a serif at the top of the arc. This serif w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2d Oc Rhombic
D, or d, is the fourth letter in the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''dee'' (pronounced ), plural ''dees''. History The Semitic letter Dāleth may have developed from the logogram for a fish or a door. There are many different Egyptian hieroglyphs that might have inspired this. In Semitic, Ancient Greek and Latin, the letter represented ; in the Etruscan alphabet the letter was archaic, but still retained (see letter B). The equivalent Greek letter is Delta, Δ. Architecture The minuscule (lower-case) form of 'd' consists of a lower-story left bowl and a stem ascender. It most likely developed by gradual variations on the majuscule (capital) form 'D', and today now composed as a stem with a full lobe to the right. In handwriting, it was common to start the arc to the left of the vertical stroke, resulting in a serif at the top of the arc. This serif w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombus
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after the French sweet – also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle. Every rhombus is simple (non-self-intersecting), and is a special case of a parallelogram and a kite. A rhombus with right angles is a square. Etymology The word "rhombus" comes from grc, ῥόμβος, rhombos, meaning something that spins, which derives from the verb , romanized: , meaning "to turn round and round." The word was used both by Eucl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ''ABCD'' would be denoted . Characterizations A convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals) * A convex quadrilateral with successiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containing a right angle. A rectangle with four sides of equal length is a ''square''. The term "oblong" is occasionally used to refer to a non-square rectangle. A rectangle with vertices ''ABCD'' would be denoted as . The word rectangle comes from the Latin ''rectangulus'', which is a combination of ''rectus'' (as an adjective, right, proper) and ''angulus'' (angle). A crossed rectangle is a crossed (self-intersecting) quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals (therefore only two sides are parallel). It is a special case of an antiparallelogram, and its angles are not right angles and not all equal, though opposite angles are equal. Other geometries, such as spherical, elliptic, and hyperboli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |