 |
Petrie Dual
In topological graph theory, the Petrie dual of an embedded graph (on a 2-manifold with all faces disks) is another embedded graph that has the Petrie polygons of the first embedding as its faces. The Petrie dual is also called the Petrial, and the Petrie dual of an embedded graph G may be denoted G^\pi. It can be obtained from a signed rotation system or ribbon graph representation of the embedding by twisting every edge of the embedding. Properties Like the usual dual graph, repeating the Petrie dual operation twice returns to the original surface embedding. Unlike the usual dual graph (which is an embedding of a generally different graph in the same surface) the Petrie dual is an embedding of the same graph in a generally different surface. Surface duality and Petrie duality are two of the six Wilson operations, and together generate the group of these operations. Regular polyhedra Applying the Petrie dual to a regular polyhedron produces a regular map. The number of skew ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Regular Dodecahedron
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals (60 face diagonals, 100 space diagonals). It is represented by the Schläfli symbol . Dimensions If the edge length of a regular dodecahedron is a, the radius of a circumscribed sphere (one that touches the regular dodecahedron at all vertices) is :r_u = a\frac \left(1 + \sqrt\right) \approx 1.401\,258\,538 \cdot a and the radius of an inscribed sphere (tangent to each of the regular dodecahedron's faces) is :r_i = a\frac \sqrt \approx 1.113\,516\,364 \cdot a while the midradius, which touches the middle of each edge, is :r_m = a\frac \left(3 +\sqrt\right) \approx 1.309\,016\,994 \cdot a These quantities may also be expressed as :r_u = a\, \frac \phi :r_i = a\, \frac :r_m = a\, \frac where ''ϕ'' is the golden ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Hemi-cube (geometry)
In abstract geometry, a hemicube is an abstract, regular polyhedron, containing half the faces of a cube. Realization It can be realized as a projective polyhedron (a tessellation of the real projective plane by three quadrilaterals), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. It has three square faces, six edges, and four vertices. It has an unexpected property that every face is in contact with every other face on two edges, and every face contains all the vertices, which gives an example of an abstract polytope whose faces are not determined by their vertex sets. From the point of view of graph theory the skeleton is a tetrahedral graph, an embedding of ''K''4 (the complete graph with four vertices) on a projective plane. The hemicube should not be confused with the demicube – the hemicube is a projective polyhedron, while the demic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
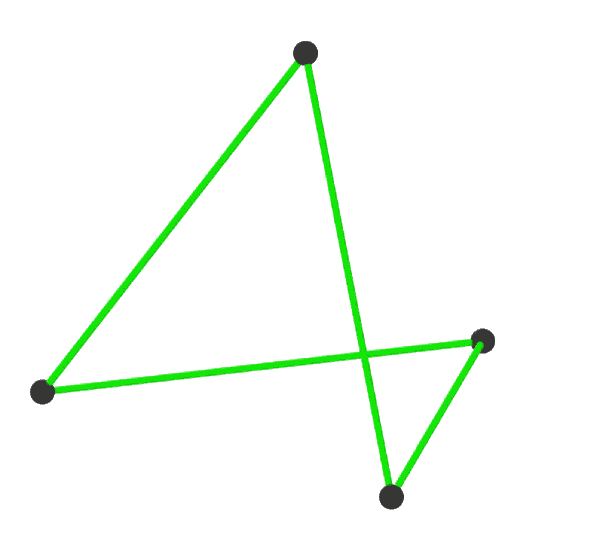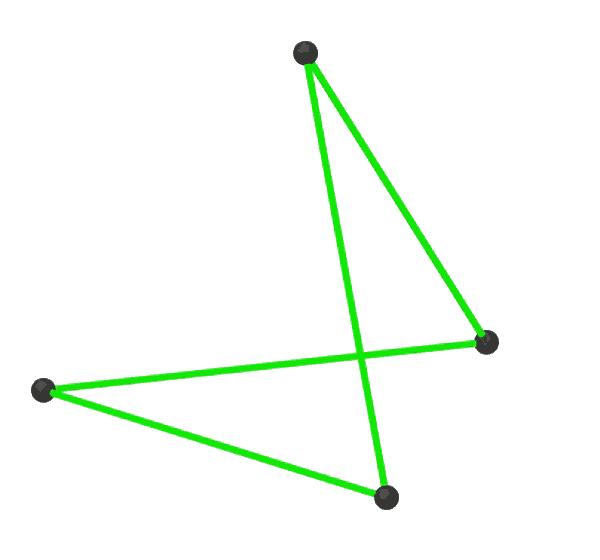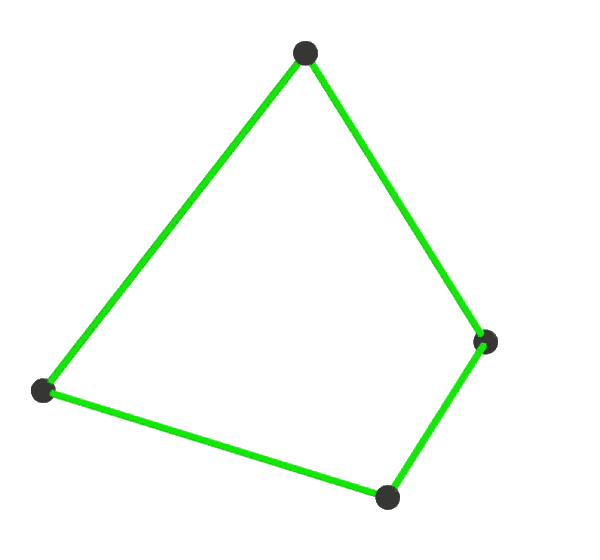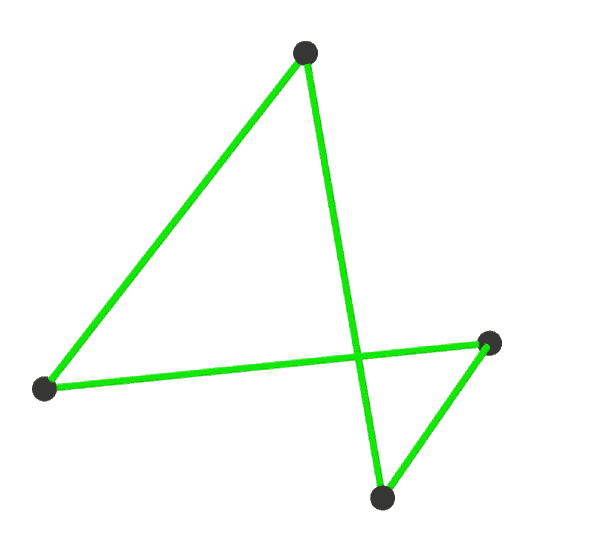
Petrial Icosahedron
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is identified by its Schläfli symbol of the form , where ''n'' is the number of sides of each face and ''m'' the number of faces meeting at each vertex. There are 5 finite convex regular polyhedra (the Platonic solids), and four regular star polyhedra (the Kepler–Poinsot polyhedra), making nine regular polyhedra in all. In addition, there are five regular compounds of the regular polyhedra. The regular polyhedra There are five convex regular polyhedra, known as the Platonic solids, four regular star polyhedra, the Kepler–Poinsot polyhedra, and five regular compo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Petrial Dodecahedron
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is identified by its Schläfli symbol of the form , where ''n'' is the number of sides of each face and ''m'' the number of faces meeting at each vertex. There are 5 finite convex regular polyhedra (the Platonic solids), and four regular star polyhedra (the Kepler–Poinsot polyhedra), making nine regular polyhedra in all. In addition, there are five regular compounds of the regular polyhedra. The regular polyhedra There are five convex regular polyhedra, known as the Platonic solids, four regular star polyhedra, the Kepler–Poinsot polyhedra, and five regular compoun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Octahedron 4 Petrie Polygons
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. A regular octahedron is the dual polyhedron of a cube. It is a rectified tetrahedron. It is a square bipyramid in any of three orthogonal orientations. It is also a triangular antiprism in any of four orientations. An octahedron is the three-dimensional case of the more general concept of a cross polytope. A regular octahedron is a 3-ball in the Manhattan () metric. Regular octahedron Dimensions If the edge length of a regular octahedron is ''a'', the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is :r_u = \frac a \approx 0.707 \cdot a and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is :r_i = \frac a \approx 0.408\cdot a while the midradius, which tou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Cube 4 Petrie Polygons
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3-zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spherical tiling, and pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg) |
Tetrahedron 3 Petrie Polygons
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another spher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Face Of Petrial Icosahedron
The face is the front of an animal's head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affect the psyche adversely. Structure The front of the human head is called the face. It includes several distinct areas, of which the main features are: *The forehead, comprising the skin beneath the hairline, bordered laterally by the temples and inferiorly by eyebrows and ears *The eyes, sitting in the orbit and protected by eyelids and eyelashes * The distinctive human nose shape, nostrils, and nasal septum *The cheeks, covering the maxilla and mandibula (or jaw), the extremity of which is the chin *The mouth, with the upper lip divided by the philtrum, sometimes revealing the teeth Facial appearance is vital for human recognition and communication. Facial muscles in humans allow expression of emotions. The face is itself a highly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Face Of Petrial Dodecahedron
The face is the front of an animal's head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human Personal identity, identity, and damage such as scarring or developmental deformities may affect the psyche adversely. Structure The front of the human head is called the face. It includes several distinct areas, of which the main features are: *The forehead, comprising the human skin, skin beneath the hairline, bordered laterally by the temple (anatomy), temples and inferiorly by eyebrows and ears *The Human eye, eyes, sitting in the orbit (anatomy), orbit and protected by eyelids and eyelashes * The distinctive human nose Ethmoid bone, shape, nostrils, and nasal septum *The cheeks, covering the maxilla and mandibula (or jaw), the extremity of which is the chin *The Human mouth, mouth, with the upper lip divided by the philtrum, sometimes revealing the tooth, teeth Facial biometrics, appearance is vital for hum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Face Of Petrial Octahedron
The face is the front of an animal's head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affect the psyche adversely. Structure The front of the human head is called the face. It includes several distinct areas, of which the main features are: *The forehead, comprising the skin beneath the hairline, bordered laterally by the temples and inferiorly by eyebrows and ears *The eyes, sitting in the orbit and protected by eyelids and eyelashes * The distinctive human nose shape, nostrils, and nasal septum *The cheeks, covering the maxilla and mandibula (or jaw), the extremity of which is the chin *The mouth, with the upper lip divided by the philtrum, sometimes revealing the teeth Facial appearance is vital for human recognition and communication. Facial muscles in humans allow expression of emotions. The face is itself a highl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |