|
Peres–Horodecki Criterion
The Peres–Horodecki criterion is a necessary condition, for the joint density matrix \rho of two quantum mechanical systems A and B, to be separable. It is also called the PPT criterion, for ''positive partial transpose''. In the 2×2 and 2×3 dimensional cases the condition is also sufficient. It is used to decide the separability of mixed states, where the Schmidt decomposition does not apply. The theorem was discovered in 1996 by Asher Peres and the Horodecki family (Michał, Paweł, and Ryszard) In higher dimensions, the test is inconclusive, and one should supplement it with more advanced tests, such as those based on entanglement witnesses. Definition If we have a general state \rho which acts on \mathcal_A \otimes \mathcal_B :\rho = \sum_ p^_ , i\rangle \langle j , \otimes , k\rangle \langle l, Its partial transpose (with respect to the B party) is defined as :\rho^ := (I \otimes T) (\rho) = \sum_ p^ _ , i\rangle \langle j , \otimes (, k\rangle \langle l, )^T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density Matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using the Born rule. It is a generalization of the more usual state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent ''mixed states''. Mixed states arise in quantum mechanics in two different situations: first when the preparation of the system is not fully known, and thus one must deal with a statistical ensemble of possible preparations, and second when one wants to describe a physical system which is entangled with another, without describing their combined state. Density matrices are thus crucial tools in areas of quantum mechanics that deal with mixed states, such as quantum statistical mechanics, open quantum systems, quantum decoherence, and quantum information. Definition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Werner State
A Werner state is a -dimensional bipartite quantum state density matrix that is invariant under all unitary operators of the form U \otimes U. That is, it is a bipartite quantum state \rho_ that satisfies :\rho_ = (U \otimes U) \rho_ (U^\dagger \otimes U^\dagger) for all unitary operators ''U'' acting on ''d''-dimensional Hilbert space. These states were first developed by Reinhard F. Werner in 1989. General definition Every Werner state W_^ is a mixture of projectors onto the symmetric and antisymmetric subspaces, with the relative weight p \in ,1/math> being the main parameter that defines the state, in addition to the dimension d \geq 2: :W_^ = p \frac P^\text_ + (1-p) \frac P^\text_, where :P^\text_ = \frac(I_+F_), :P^\text_ = \frac(I_-F_), are the projectors and :F_ = \sum_ , i\rangle \langle j, _A \otimes , j\rangle \langle i, _B is the permutation or flip operator that exchanges the two subsystems ''A'' and ''B''. Werner states are separable for ''p'' ≥ and entang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rajiah Simon
Rajiah Simon, is a Professor of Physics at the Institute of Mathematical Sciences, Chennai, India. Rajiah Simon received the Shanti Swarup Bhatnagar Prize for Science and Technology in 1993 for pioneering work in Quantum optics. Simon and collaborators initiated the "Quantum theory of charged-particle beam optics", by working out the focusing action of a magnetic quadrupole using the Dirac Equation. R. Jagannathan, R. Simon, E. C. G. Sudarshan Ennackal Chandy George Sudarshan (also known as E. C. G. Sudarshan; 16 September 1931 – 13 May 2018) was an Indian American theoretical physicist and a professor at the University of Texas. Sudarshan has been credited with numerous contrib ... and N. MukundaQuantum theory of magnetic electron lenses based on the Dirac equation Physics Letters A, 134, 457-464 (1989). References External links [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Communication
Quantum information science is an interdisciplinary field that seeks to understand the analysis, processing, and transmission of information using quantum mechanics principles. It combines the study of Information science with quantum effects in physics. It includes theoretical issues in computational models and more experimental topics in quantum physics, including what can and cannot be done with quantum information. The term quantum information theory is also used, but it fails to encompass experimental research, and can be confused with a subfield of quantum information science that addresses the processing of quantum information. Scientific and engineering studies To understand quantum teleportation, quantum entanglement and the manufacturing of quantum computer hardware requires a thorough understanding of quantum physics and engineering. Since 2010s, there has been remarkable progress in manufacturing quantum computers, with companies like Google and IBM investing heavily ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entanglement Distillation
Entanglement distillation (also called ''entanglement purification'') is the transformation of ''N'' copies of an arbitrary entangled state \rho into some number of approximately pure Bell pairs, using only local operations and classical communication. Quantum entanglement distillation can in this way overcome the degenerative influence of noisy quantum channels by transforming previously shared less entangled pairs into a smaller number of maximally entangled pairs. History The limits for entanglement dilution and distillation are due to C. H. Bennett, H. Bernstein, S. Popescu, and B. Schumacher, who presented the first distillation protocols for pure states in 1996; entanglement distillation protocols for mixed states were introduced by Bennett, Brassard, Popescu, Schumacher, Smolin and Wootters the same year. Bennett, DiVincenzo, Smolin and Wootters established the connection to quantum error-correction in a ground-breaking paper published in August 1996, also in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bound Entanglement
Bound entanglement is a weak form of quantum entanglement, from which no singlets can be distilled with local operations and classical communication (LOCC). Bound entanglement was discovered by M. Horodecki, P. Horodecki, and R. Horodecki. Bipartite entangled states that have a non-negative partial transpose are all bound-entangled. Moreover, a particular quantum state for 2x4 systems has been presented. Such states are not detected by the Peres-Horodecki criterion as entangled, thus other entanglement criteria are needed for their detection. There are a number of examples for such states. There are also multipartite entangled states that have a negative partial transpose with respect to some bipartitions, while they have a positive partial transpose to the other partitions, nevertheless, they are undistillable. The possible existence of bipartite bound entangled states with a negative partial transpose is still under intensive study. Properties of bound entangled states with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Choi's Theorem On Completely Positive Maps
In mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional (matrix) C*-algebras. An infinite-dimensional algebraic generalization of Choi's theorem is known as Belavkin's " Radon–Nikodym" theorem for completely positive maps. Statement Choi's theorem. Let \Phi : \mathbb^ \to \mathbb^ be a linear map. The following are equivalent: :(i) is -positive (i.e. \left (\operatorname_n\otimes\Phi \right )(A)\in\mathbb^\otimes\mathbb^ is positive whenever A\in\mathbb^\otimes\mathbb^ is positive). :(ii) The matrix with operator entries ::C_\Phi= \left (\operatorname_n\otimes\Phi \right ) \left (\sum_E_\otimes E_ \right ) = \sum_E_\otimes\Phi(E_) \in \mathbb ^ :is positive, where E_ \in \mathbb^ is the matrix with 1 in the -th entry and 0s elsewhere. (The matrix ''C''Φ is sometimes called the ''Choi matrix'' of .) :(iii) is completely positive. Proof (i) implies (ii) We observe that if :E=\sum_E_\oti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hahn–Banach Theorem
The Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed vector space to make the study of the dual space "interesting". Another version of the Hahn–Banach theorem is known as the Hahn–Banach separation theorem or the hyperplane separation theorem, and has numerous uses in convex geometry. History The theorem is named for the mathematicians Hans Hahn and Stefan Banach, who proved it independently in the late 1920s. The special case of the theorem for the space C , b/math> of continuous functions on an interval was proved earlier (in 1912) by Eduard Helly, and a more general extension theorem, the M. Riesz extension theorem, from which the Hahn–Banach theorem can be derived, was proved in 1923 by Marcel Riesz. The first Hahn–Banach theorem was prov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximally Entangled State
Quantum entanglement is the phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics. Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior gives r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
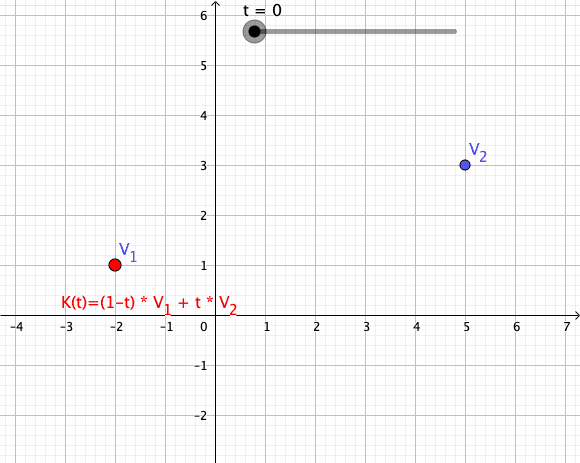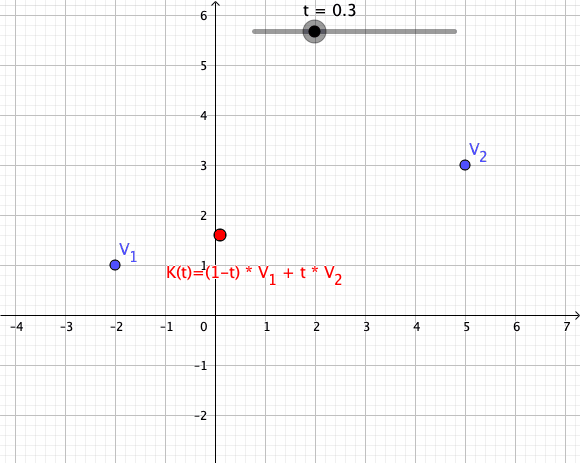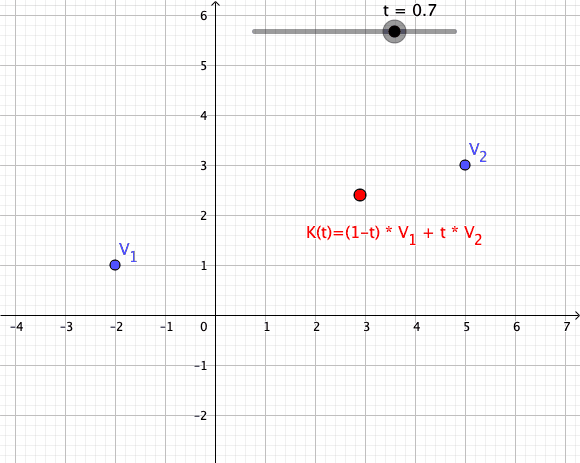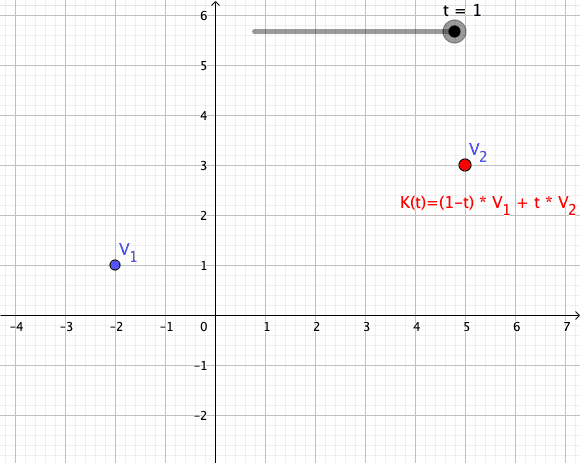
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is id ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Entanglement
Quantum entanglement is the phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics. Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior gives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |