|
Pareto Set
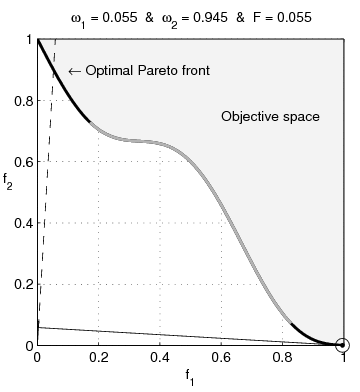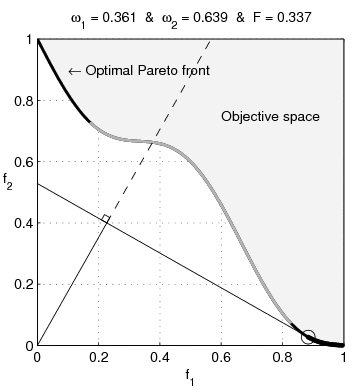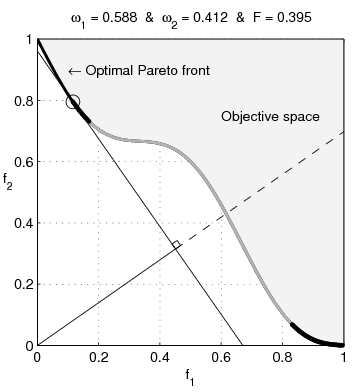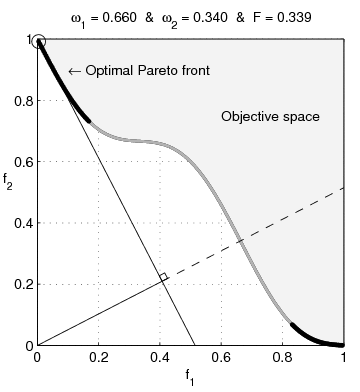
In multi-objective optimization, the Pareto front (also called Pareto frontier or Pareto curve) is the set of all Pareto efficient solutions. The concept is widely used in engineering. It allows the designer to restrict attention to the set of efficient choices, and to make tradeoffs within this set, rather than considering the full range of every parameter. Definition The Pareto frontier, ''P''(''Y''), may be more formally described as follows. Consider a system with function f: X \rightarrow \mathbb^m, where ''X'' is a compact set of feasible decisions in the metric space \mathbb^n, and ''Y'' is the feasible set of criterion vectors in \mathbb^m, such that Y = \. We assume that the preferred directions of criteria values are known. A point y^ \in \mathbb^m is preferred to (strictly dominates) another point y^ \in \mathbb^m, written as y^ \succ y^. The Pareto frontier is thus written as: : P(Y) = \. Marginal rate of substitution A significant aspect of the Pareto frontie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multi-objective Optimization
Multi-objective optimization or Pareto optimization (also known as multi-objective programming, vector optimization, multicriteria optimization, or multiattribute optimization) is an area of MCDM, multiple-criteria decision making that is concerned with Mathematical optimization, mathematical optimization problems involving more than one Loss function, objective function to be optimized simultaneously. Multi-objective is a type of vector optimization that has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Space
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces. One suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hausdorff Distance
In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty set, non-empty compact space, compact subsets of a metric space into a metric space in its own right. It is named after Felix Hausdorff and Dimitrie Pompeiu. Informally, two sets are close in the Hausdorff distance if every point of either set is close to some point of the other set. The Hausdorff distance is the longest distance someone can be forced to travel by an adversary who chooses a point in one of the two sets, from where they then must travel to the other set. In other words, it is the greatest of all the distances from a point in one set to the closest point in the other set. This distance was first introduced by Hausdorff in his book ''Grundzüge der Mengenlehre'', first published in 1914, although a very close relative appeared in the doctoral thesis of Maurice René Fré ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skyline Operator
The skyline operator is the subject of an optimization problem and computes the Pareto optimum on tuples with multiple dimensions. This operator is an extension to SQL proposed by Börzsönyi et al. to filter results from a database to keep only those objects that are not dominated by any other point on all dimensions. The name ''skyline'' comes from the view on Manhattan from the Hudson River, where those buildings can be seen that are not hidden by any other. A building is visible if it is not dominated by a building that is taller or closer to the river (two dimensions, distance to the river minimized, height maximized). Another application of the skyline operator involves selecting a hotel for a holiday. The user wants the hotel to be both cheap and close to the beach. However, hotels that are close to the beach may also be expensive. In this case, the skyline operator would only present those hotels that are not worse than any other hotel in both price and distance to the beac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxima Of A Point Set
In computational geometry, a point in a finite set of points is said to be ''maximal'' or ''non-dominated'' if there is no other point in whose coordinates are all greater than or equal to the corresponding coordinates of . The maxima of a point set are all the maximal points of . The problem of finding all maximal points, sometimes called the problem of the maxima or maxima set problem, has been studied as a variant of the convex hull and orthogonal convex hull problems. It is equivalent to finding the Pareto frontier of a collection of points, and was called the floating-currency problem by Herbert Freeman based on an application involving comparing the relative wealth of individuals with different holdings of multiple currencies.. Two dimensions For points in two dimensions, this problem can be solved in time by an algorithm that performs the following steps: *Sort the points in one of the coordinate dimensions (the -coordinate, say) *For each point, in decreasing order ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the d'Alembert principle of virtual work. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the Turin Academy of Science in 1760 culminating in his 1788 grand opus, ''Mécanique analytique''. Lagrangian mechanics describes a mechanical system as a pair consisting of a configuration space (physics), configuration space ''M'' and a smooth function L within that space called a ''Lagrangian''. For many systems, , where ''T'' and ''V'' are the Kinetic energy, kinetic and Potential energy, potential energy of the system, respectively. The stationary action principle requires that the Action (physics)#Action (functional), action functional of the system derived from ''L'' must remain at a stationary point (specifically, a Maximum and minimum, maximum, Maximum and minimum, minimum, or Saddle point, saddle point) throughout the time evoluti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marginal Rate Of Substitution
In economics, the marginal rate of substitution (MRS) is the rate at which a consumer can give up some amount of one good in exchange for another good while maintaining the same level of utility. At equilibrium consumption levels (assuming no externalities), marginal rates of substitution are identical. The marginal rate of substitution is one of the three factors from marginal productivity, the others being marginal rates of transformation and marginal productivity of a factor. As the slope of indifference curve Under the standard assumption of neoclassical economics that goods and services are continuously divisible, the marginal rates of substitution will be the same regardless of the direction of exchange, and will correspond to the slope of an indifference curve (more precisely, to the slope multiplied by −1) passing through the consumption bundle in question, at that point: mathematically, it is the implicit derivative. MRS of X for Y is the amount of Y which a consumer c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), function called a metric or distance function. Metric spaces are a general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a Conceptual metaphor , metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different bra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pareto Efficient Frontier 1024x1024
Pareto may refer to: People * Vilfredo Pareto (1848–1923), Italian economist, political scientist, and philosopher, works named for him include: ** Pareto analysis, a statistical analysis tool in problem solving **Pareto distribution, a power-law probability distribution **Pareto efficiency ** Pareto front, the set of all Pareto efficient solutions ** Pareto principle, or the 80-20 rule * Bartolomeo Pareto, medieval priest and cartographer from Genoa * Graziella Pareto (1889–1973), Catalan soprano * Lorenzo Pareto Lorenzo Nicolò Pareto (Genoa, 6 December 1800 – Genoa, 19 June 1865) was an Italian geologist and statesman. As a man of science, he is considered one of the fathers of modern geology. A member of the Italian National Academy of Sciences, h ... (1800–1865), Italian geologist and statesman * Paula Pareto (born 1986), Argentine judoka * Benedetto Pareto, builder of the Shrine of Nostra Signora della Guardia in Liguria, Italy Other uses * Pareto, Piedmo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pareto Efficient
In welfare economics, a Pareto improvement formalizes the idea of an outcome being "better in every possible way". A change is called a Pareto improvement if it leaves at least one person in society better off without leaving anyone else worse off than they were before. A situation is called Pareto efficient or Pareto optimal if all possible Pareto improvements have already been made; in other words, there are no longer any ways left to make one person better off without making some other person worse-off. In social choice theory, the same concept is sometimes called the unanimity principle, which says that if ''everyone'' in a society ( non-strictly) prefers A to B, society as a whole also non-strictly prefers A to B. The Pareto front consists of all Pareto-efficient situations. In addition to the context of efficiency in ''allocation'', the concept of Pareto efficiency also arises in the context of ''efficiency in production'' vs. '' x-inefficiency'': a set of outputs of go ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |