|
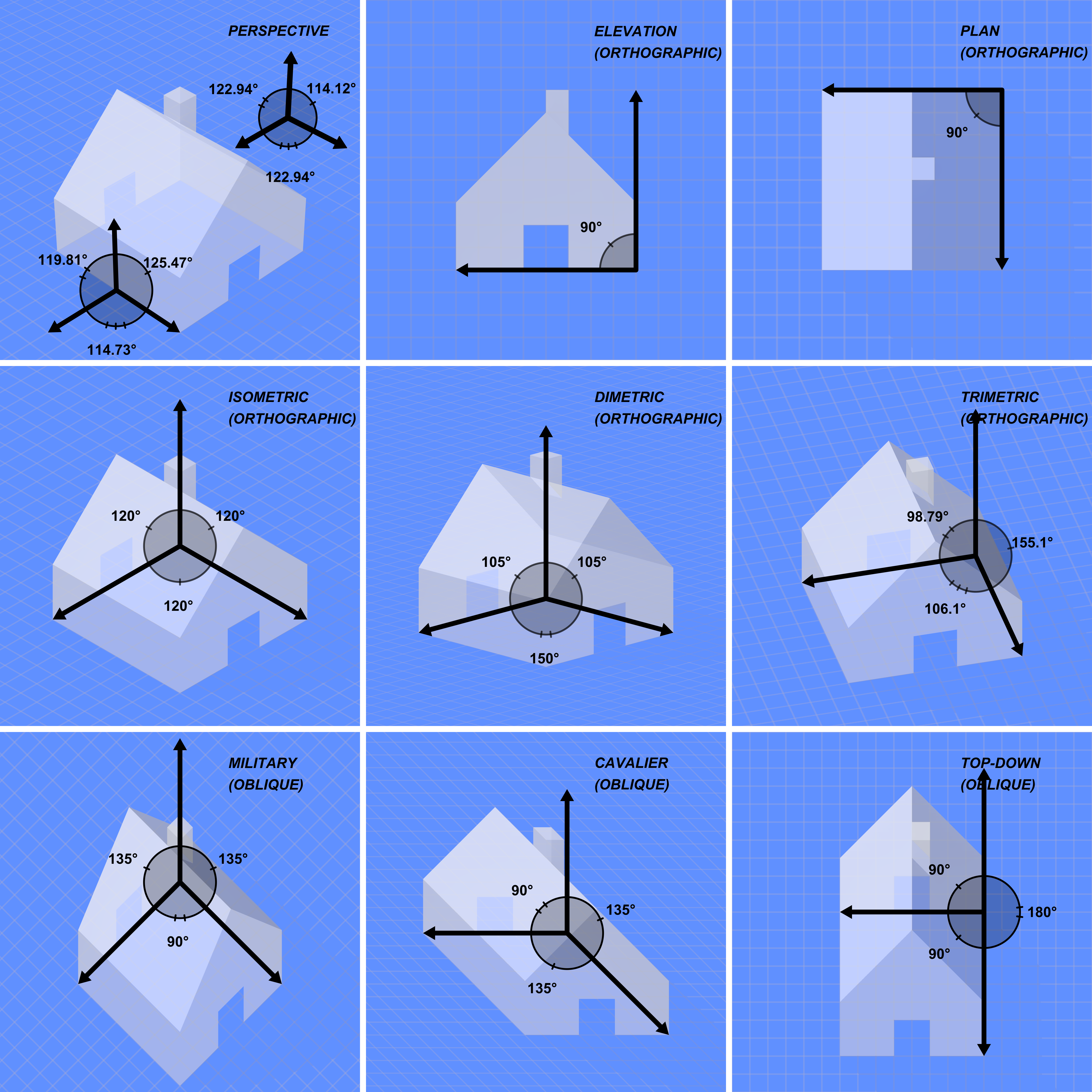
Orthographic Projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing three-dimensional objects in two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''Axonometric projection'' is synonymous with ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiview Projection
In technical drawing and computer graphics, a multiview projection is a technique of illustration by which a standardized series of orthographic two-dimensional pictures are constructed to represent the form of a three-dimensional object. Up to six pictures of an object are produced (called ''primary views''), with each projection plane parallel to one of the coordinate axes of the object. The views are positioned relative to each other according to either of two schemes: ''first-angle'' or ''third-angle'' projection. In each, the appearances of views may be thought of as being ''projected'' onto planes that form a six-sided box around the object. Although six different sides can be drawn, ''usually'' three views of a drawing give enough information to make a three-dimensional object. These views are known as ''front view'', ''top view'' and ''end view''. Other names for these views include ''plan'', ''elevation'' and ''section''. When the plane or axis of the object depicted ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analemma
In astronomy, an analemma (; ) is a diagram showing the position of the Sun in the sky as seen from a fixed location on Earth at the same mean solar time, as that position varies over the course of a year. The diagram will resemble a figure eight. Globes of Earth often display an analemma as a two-dimensional figure of equation of time vs. declination of the Sun. The north–south component of the analemma results from the change in the Sun's declination due to the tilt of Earth's axis of rotation. The east–west component results from the nonuniform rate of change of the Sun's right ascension, governed by combined effects of Earth's axial tilt and orbital eccentricity. One can photograph an analemma by keeping a camera at a fixed location and orientation and taking multiple exposures throughout the year, always at the same time of day (disregarding daylight saving time, if applicable). Diagrams of analemmas frequently carry marks that show the position of the Su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-tuple
In mathematics, a tuple is a finite ordered list (sequence) of elements. An -tuple is a sequence (or ordered list) of elements, where is a non-negative integer. There is only one 0-tuple, referred to as ''the empty tuple''. An -tuple is defined inductively using the construction of an ordered pair. Mathematicians usually write tuples by listing the elements within parentheses "" and separated by a comma and a space; for example, denotes a 5-tuple. Sometimes other symbols are used to surround the elements, such as square brackets " nbsp; or angle brackets "⟨ ⟩". Braces "" are used to specify arrays in some programming languages but not in mathematical expressions, as they are the standard notation for sets. The term ''tuple'' can often occur when discussing other mathematical objects, such as vectors. In computer science, tuples come in many forms. Most typed functional programming languages implement tuples directly as product types, tightly associated with algeb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perspective Projection
Linear or point-projection perspective (from la, perspicere 'to see through') is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection. Linear perspective is an approximate representation, generally on a flat surface, of an image as it is seen by the eye. Perspective drawing is useful for representing a three-dimensional scene in a two-dimensional medium, like paper. The most characteristic features of linear perspective are that objects appear smaller as their distance from the observer increases, and that they are subject to ''foreshortening'', meaning that an object's dimensions along the line of sight appear shorter than its dimensions across the line of sight. All objects will recede to points in the distance, usually along the horizon line, but also above and below the horizon line depending on the view used. Italian Renaissance painters and architects including Masaccio, Paolo Uccello, Piero della Francesca and Luca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
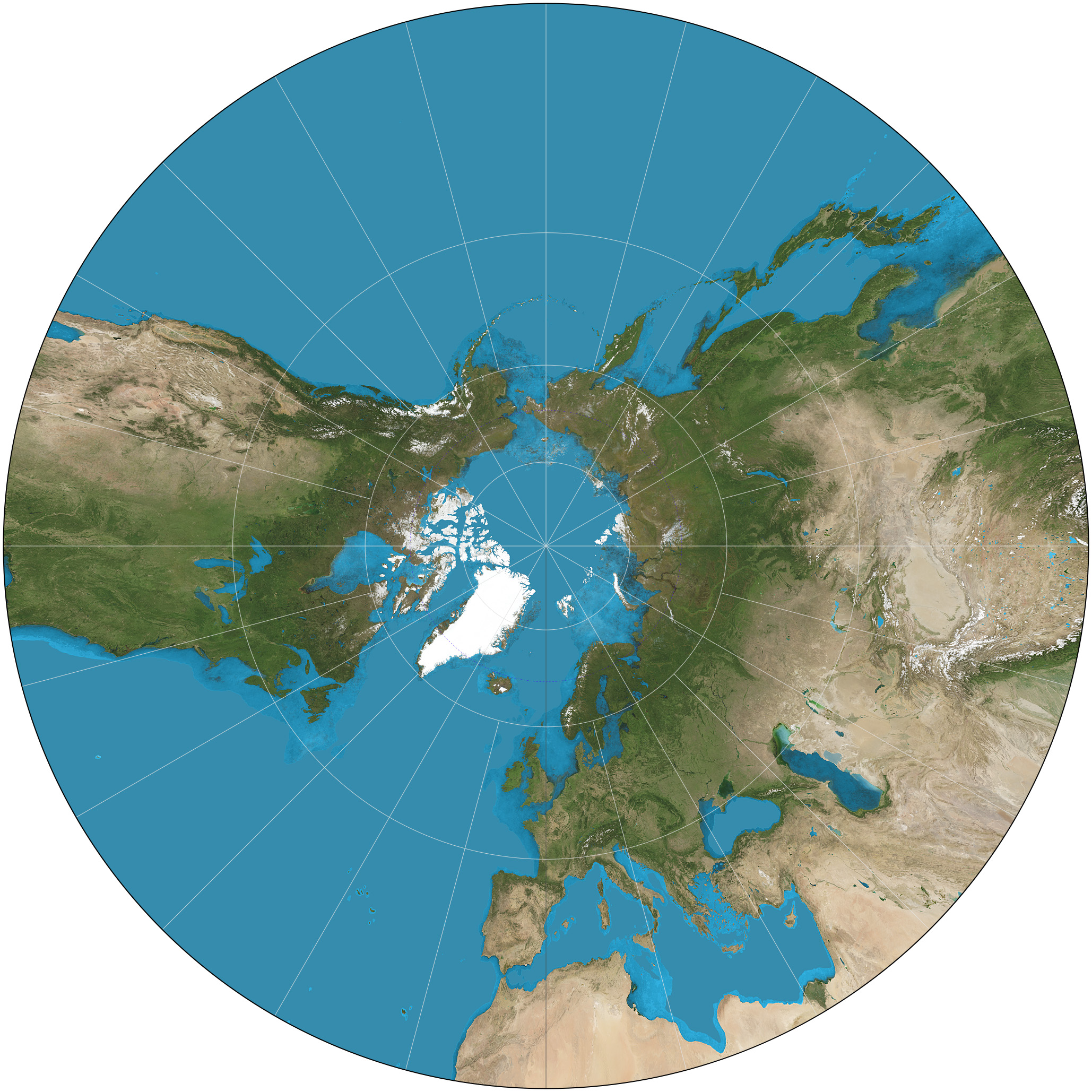
Gnomonic Projection
A gnomonic map projection is a map projection which displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. This is achieved by casting surface points of the sphere onto a tangent plane, each landing where a ray from the center of the sphere passes through the point on the surface and then on to the plane. No distortion occurs at the tangent point, but distortion increases rapidly away from it. Less than half of the sphere can be projected onto a finite map. Consequently, a rectilinear photographic lens, which is based on the gnomonic principle, cannot image more than 180 degrees. History The gnomonic projection is said to be the oldest map projection, developed by Thales for star maps in the 6th century BC. The path of the shadow-tip or light-spot in a nodus-based sundial traces out the same hyperbolae formed by parallels on a gnomonic map. Properties T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
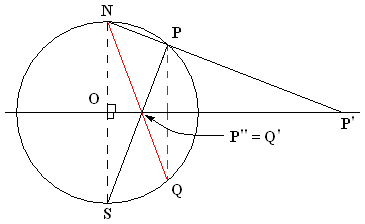
Stereographic Projection
In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere (the ''pole'' or ''center of projection''), onto a plane (the ''projection plane'') perpendicular to the diameter through the point. It is a smooth, bijective function from the entire sphere except the center of projection to the entire plane. It maps circles on the sphere to circles or lines on the plane, and is conformal, meaning that it preserves angles at which curves meet and thus locally approximately preserves shapes. It is neither isometric (distance preserving) nor equiareal (area preserving). The stereographic projection gives a way to represent a sphere by a plane. The metric induced by the inverse stereographic projection from the plane to the sphere defines a geodesic distance between points in the plane equal to the spherical distance between the spherical points they represent. A two-dimensional coordinate system on the stere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartography
Cartography (; from grc, χάρτης , "papyrus, sheet of paper, map"; and , "write") is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an imagined reality) can be modeled in ways that communicate spatial information effectively. The fundamental objectives of traditional cartography are to: * Set the map's agenda and select traits of the object to be mapped. This is the concern of map editing. Traits may be physical, such as roads or land masses, or may be abstract, such as toponyms or political boundaries. * Represent the terrain of the mapped object on flat media. This is the concern of map projections. * Eliminate characteristics of the mapped object that are not relevant to the map's purpose. This is the concern of generalization. * Reduce the complexity of the characteristics that will be mapped. This is also the concern of generalization. * Orchestrate the elements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthographic Projection SW
{{disambig ...
Orthographic may refer to: * anything related to Orthography, a linguistic discipline that studies and regulates writing systems of particular languages. ** Orthographic reform ** Orthographic transcription ** Orthographic variant ** Orthographic depth ** Orthographic Latinisation * Orthographic projection ** Orthographic projection (geometry) ** Orthographic projection (cartography) See also * Ortho (other) * -graphy The English suffix -graphy means a "field of study" or related to "writing" a book, and is an anglicization of the French ''-graphie'' inherited from the Latin ''-graphia'', which is a transliterated direct borrowing from Greek. Arts * Cartog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convention Placement Vues Dessin Technique
Convention may refer to: * Convention (norm), a custom or tradition, a standard of presentation or conduct ** Treaty, an agreement in international law * Convention (meeting), meeting of a (usually large) group of individuals and/or companies in a certain field who share a common interest ** Fan convention, a gathering of fans of a particular media property or genre ** Gaming convention, centered on role-playing games, collectible card games, miniatures wargames, board games, video games, and the like ** Political convention, a formal gathering of people for political purposes * Trade fair * Bridge convention, a term in the game of bridge * Convention (Paris Métro), a station on line 12 of the Paris Métro in the 15th arrondissement * "The Convention" (''The Office'' episode) * "Convention" (''Malcolm in the Middle'' episode) See also * Conference * National Convention (other) The National Convention was the first republican legislative body of the French Revolution, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compass And Straightedge Constructions
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses. The idealized ruler, known as a straightedge, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really means: see Markable rulers below.) More formally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perspective (graphical)
Linear or point-projection perspective (from la, perspicere 'to see through') is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection. Linear perspective is an approximate representation, generally on a flat surface, of an image as it is seen by the eye. Perspective drawing is useful for representing a three-dimensional scene in a two-dimensional medium, like paper. The most characteristic features of linear perspective are that objects appear smaller as their distance from the observer increases, and that they are subject to ''foreshortening'', meaning that an object's dimensions along the line of sight appear shorter than its dimensions across the line of sight. All objects will recede to points in the distance, usually along the horizon line, but also above and below the horizon line depending on the view used. Italian Renaissance painters and architects including Masaccio, Paolo Uccello, Piero della Francesca and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |