|
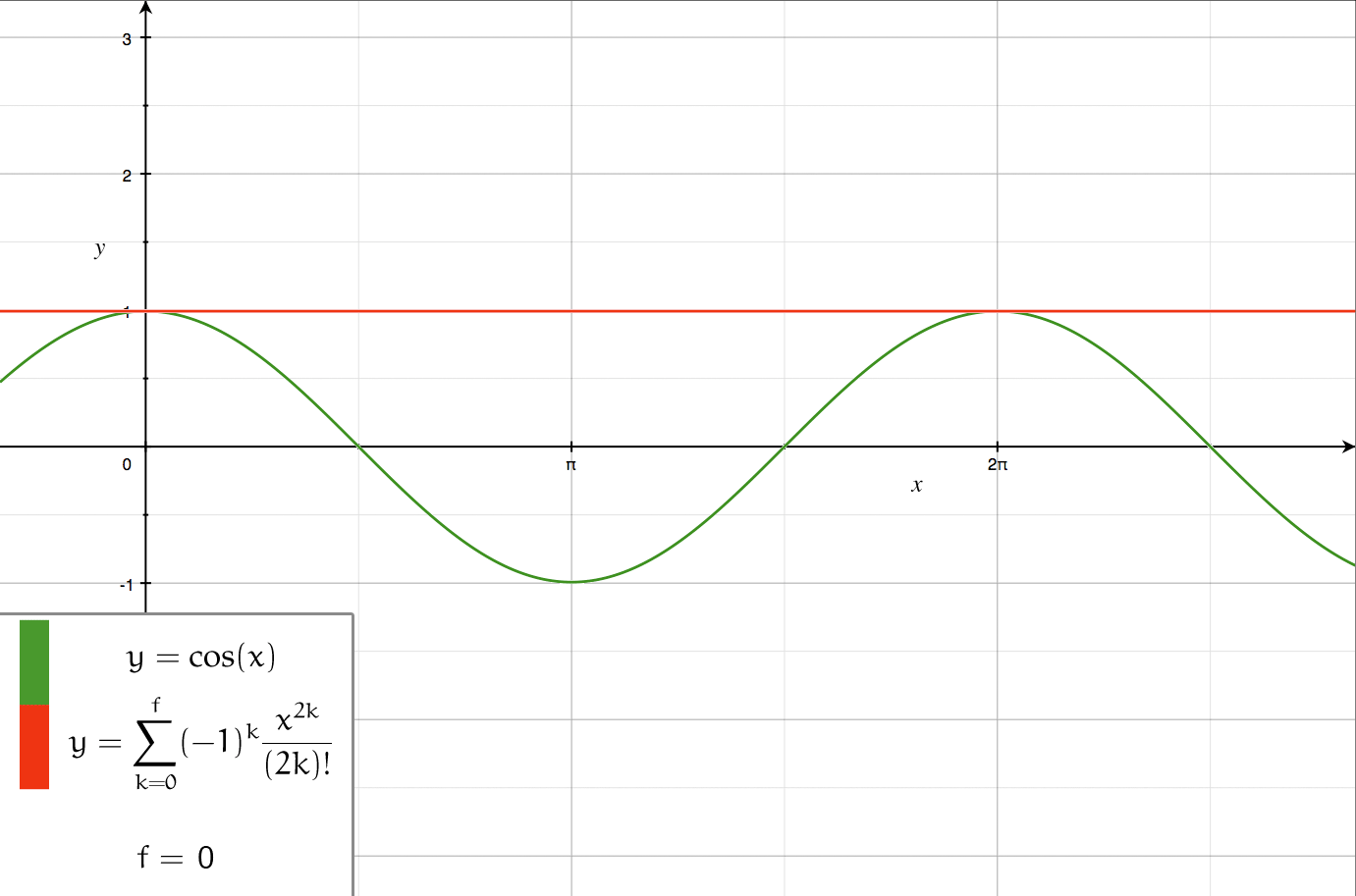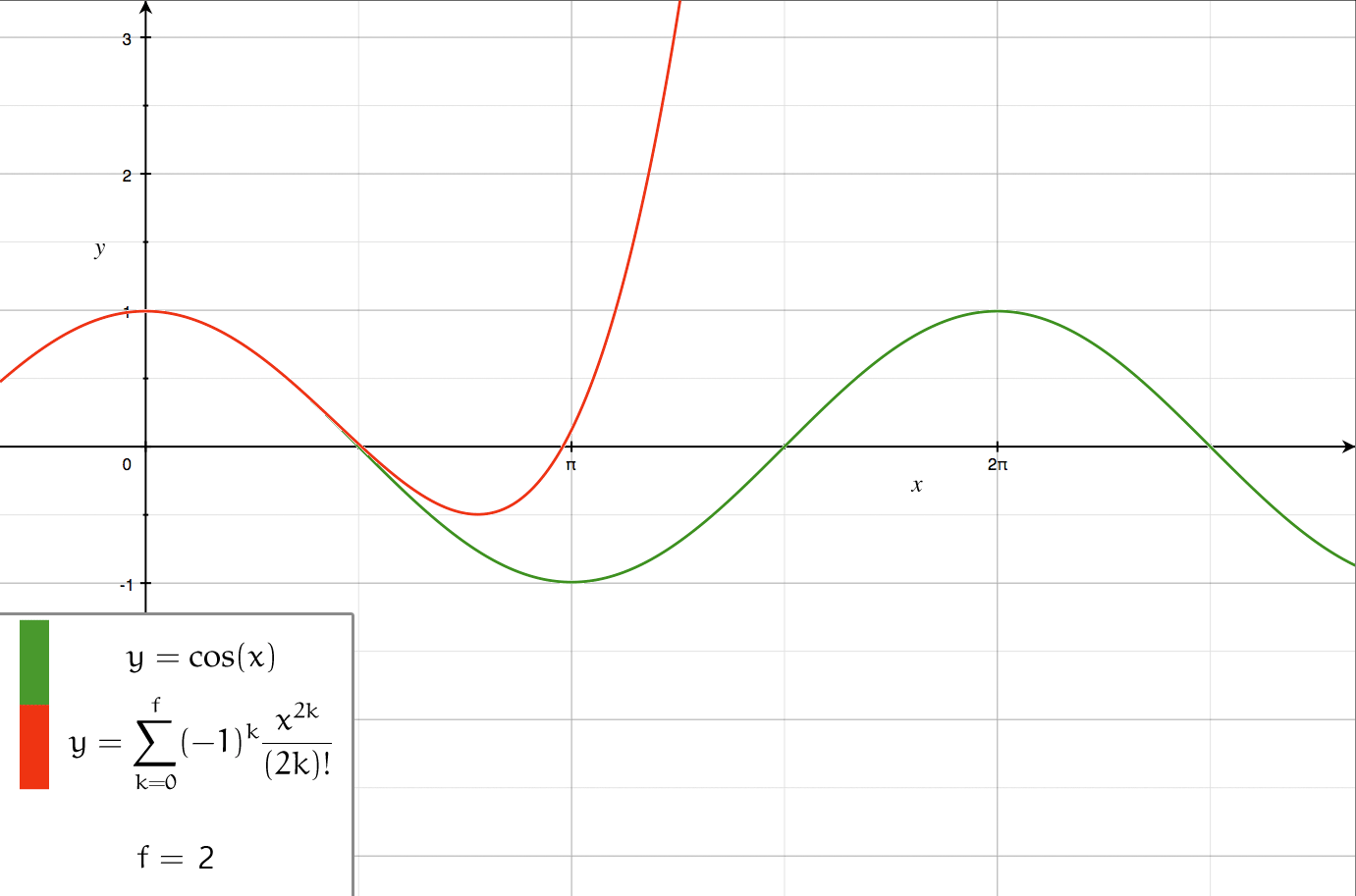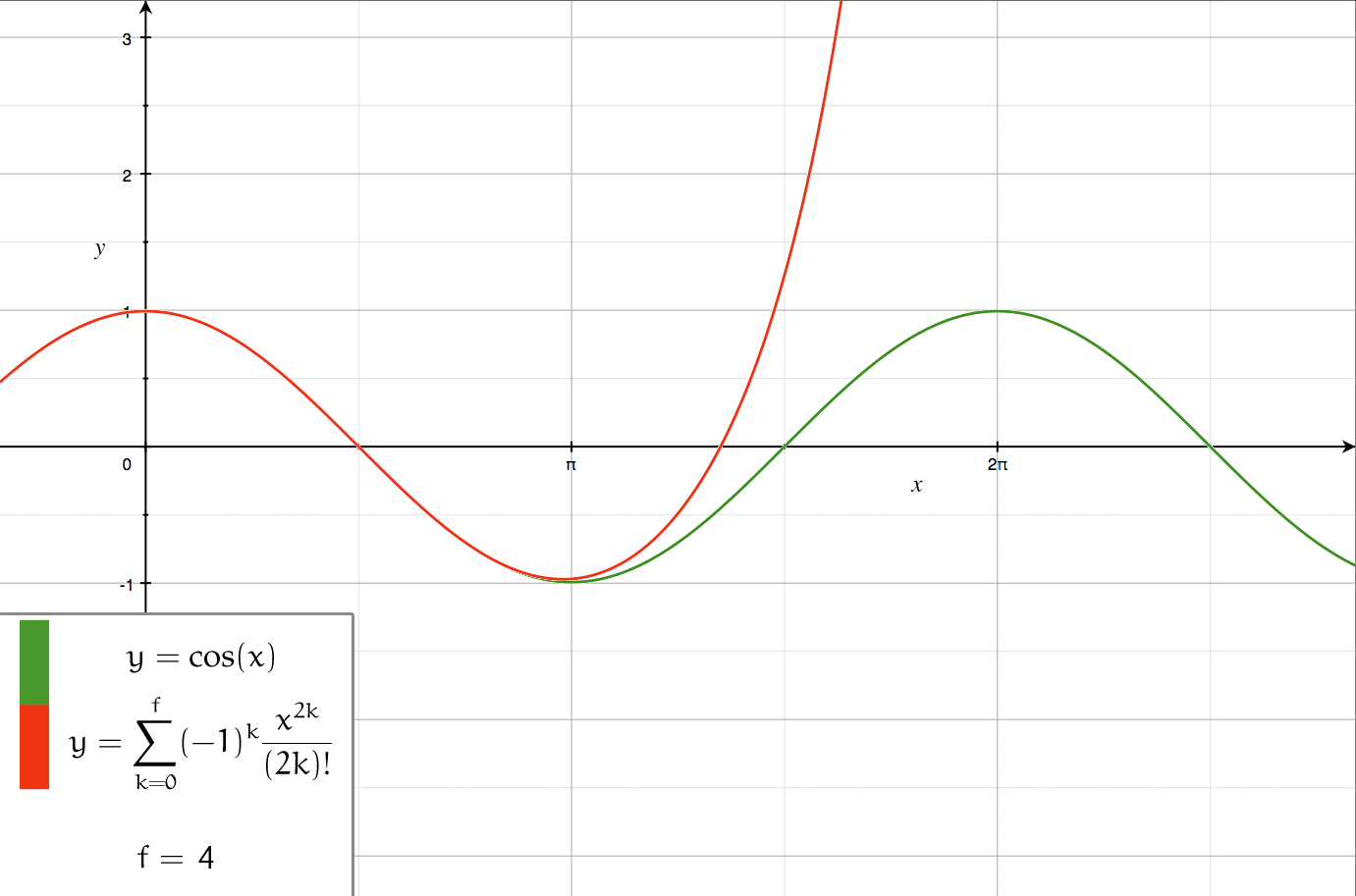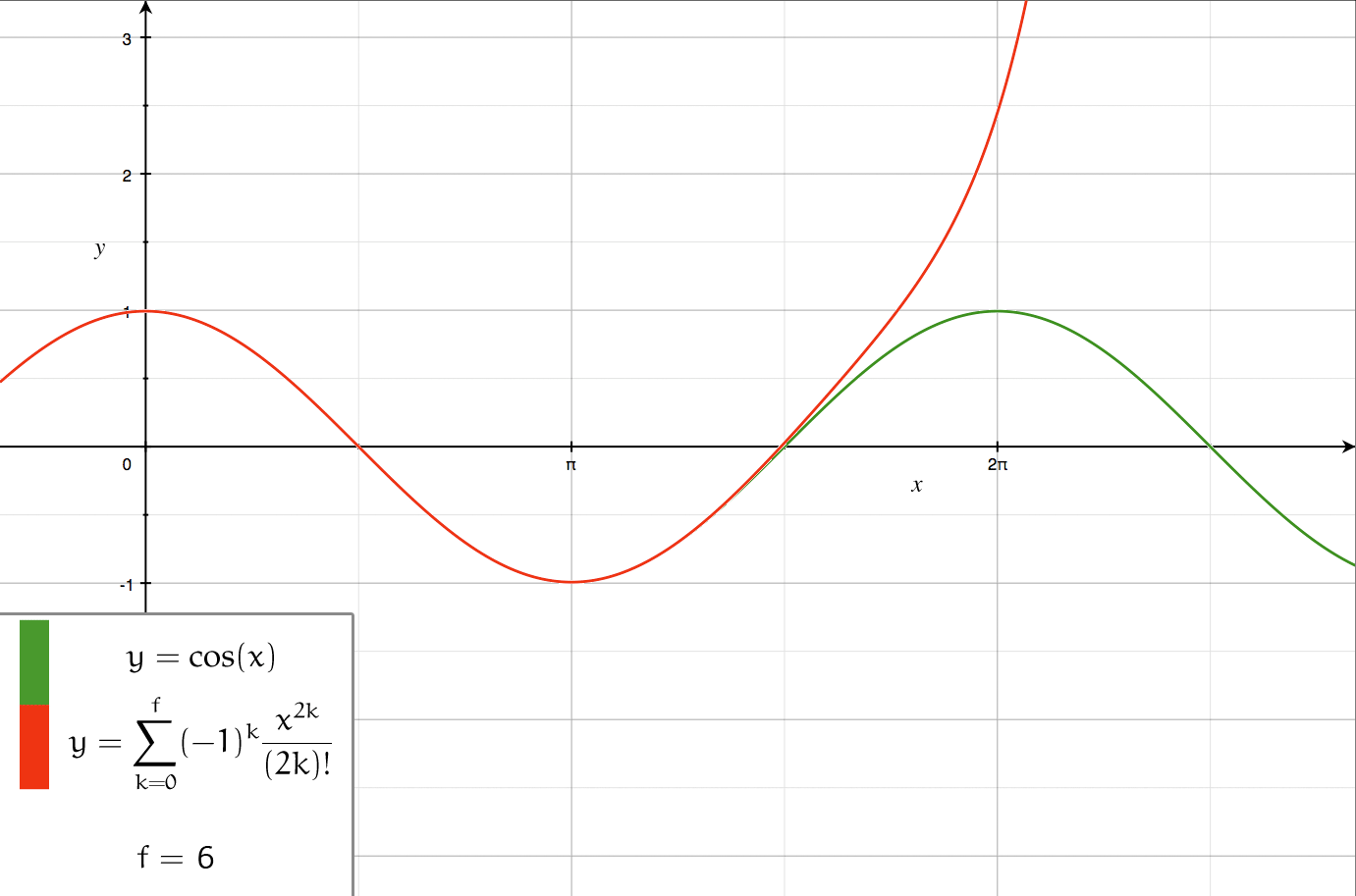
Order Of Approximation
In science, engineering, and other quantitative disciplines, order of approximation refers to formal or informal expressions for how accurate an approximation is. Usage in science and engineering In formal expressions, the ordinal number used before the word order refers to the highest power in the series expansion used in the approximation. The expressions: a ''zeroth-order approximation'', a ''first-order approximation'', a ''second-order approximation'', and so forth are used as fixed phrases. The expression a ''zero-order approximation'' is also common. Cardinal numerals are occasionally used in expressions like an ''order-zero approximation'', an ''order-one approximation'', etc. The omission of the word ''order'' leads to phrases that have less formal meaning. Phrases like first approximation or to a first approximation may refer to ''a roughly approximate value of a quantity''. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Science
Science is a systematic endeavor that Scientific method, builds and organizes knowledge in the form of Testability, testable explanations and predictions about the universe. Science may be as old as the human species, and some of the earliest archeological evidence for scientific reasoning is tens of thousands of years old. The earliest written records in the history of science come from Ancient Egypt and Mesopotamia in around 3000 to 1200 Common Era, BCE. Their contributions to mathematics, astronomy, and medicine entered and shaped Greek natural philosophy of classical antiquity, whereby formal attempts were made to provide explanations of events in the Universe, physical world based on natural causes. After the fall of the Western Roman Empire, knowledge of History of science in classical antiquity, Greek conceptions of the world deteriorated in Western Europe during the early centuries (400 to 1000 CE) of the Middle Ages, but was preserved in the Muslim world during the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Research
Research is "creative and systematic work undertaken to increase the stock of knowledge". It involves the collection, organization and analysis of evidence to increase understanding of a topic, characterized by a particular attentiveness to controlling sources of bias and error. These activities are characterized by accounting and controlling for biases. A research project may be an expansion on past work in the field. To test the validity of instruments, procedures, or experiments, research may replicate elements of prior projects or the project as a whole. The primary purposes of basic research (as opposed to applied research) are documentation, discovery, interpretation, and the research and development (R&D) of methods and systems for the advancement of human knowledge. Approaches to research depend on epistemologies, which vary considerably both within and between humanities and sciences. There are several forms of research: scientific, humanities, artistic, econ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scientist
A scientist is a person who conducts scientific research to advance knowledge in an area of the natural sciences. In classical antiquity, there was no real ancient analog of a modern scientist. Instead, philosophers engaged in the philosophical study of nature called natural philosophy, a precursor of natural science. Though Thales (circa 624-545 BC) was arguably the first scientist for describing how cosmic events may be seen as natural, not necessarily caused by gods,Frank N. Magill''The Ancient World: Dictionary of World Biography'', Volume 1 Routledge, 2003 it was not until the 19th century that the term ''scientist'' came into regular use after it was coined by the theologian, philosopher, and historian of science William Whewell in 1833. In modern times, many scientists have advanced degrees in an area of science and pursue careers in various sectors of the economy such as academia, industry, government, and nonprofit environments.'''' History The roles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Significant Figures
Significant figures (also known as the significant digits, ''precision'' or ''resolution'') of a number in positional notation are digits in the number that are reliable and necessary to indicate the quantity of something. If a number expressing the result of a measurement (e.g., length, pressure, volume, or mass) has more digits than the number of digits allowed by the measurement resolution, then only as many digits as allowed by the measurement resolution are reliable, and so only these can be significant figures. For example, if a length measurement gives 114.8 mm while the smallest interval between marks on the ruler used in the measurement is 1 mm, then the first three digits (1, 1, and 4, showing 114 mm) are certain and so they are significant figures. Digits which are uncertain but ''reliable'' are also considered significant figures. In this example, the last digit (8, which adds 0.8 mm) is also considered a significant figure even though the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percent Error
In any quantitative science, the terms relative change and relative difference are used to compare two quantities while taking into account the "sizes" of the things being compared, i.e. dividing by a ''standard'' or ''reference'' or ''starting'' value. The comparison is expressed as a ratio and is a unitless number. By multiplying these ratios by 100 they can be expressed as percentages so the terms percentage change, percent(age) difference, or relative percentage difference are also commonly used. The terms "change" and "difference" are used interchangeably. Relative change is often used as a quantitative indicator of quality assurance and quality control for repeated measurements where the outcomes are expected to be the same. A special case of percent change (relative change expressed as a percentage) called ''percent error'' occurs in measuring situations where the reference value is the accepted or actual value (perhaps theoretically determined) and the value being compared ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Accuracy And Precision
Accuracy and precision are two measures of '' observational error''. ''Accuracy'' is how close a given set of measurements (observations or readings) are to their '' true value'', while ''precision'' is how close the measurements are to each other. In other words, ''precision'' is a description of '' random errors'', a measure of statistical variability. ''Accuracy'' has two definitions: # More commonly, it is a description of only ''systematic errors'', a measure of statistical bias of a given measure of central tendency; low accuracy causes a difference between a result and a true value; ISO calls this ''trueness''. # Alternatively, ISO defines accuracy as describing a combination of both types of observational error (random and systematic), so high accuracy requires both high precision and high trueness. In the first, more common definition of "accuracy" above, the concept is independent of "precision", so a particular set of data can be said to be accurate, precise, both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series Expansion
In mathematics, a series expansion is an expansion of a function into a series, or infinite sum. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called '' series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. A ''Taylor series'' is a power series based on a function's derivatives at a single point. More specifically, if a function f: U\to\mathbb is infinitely differentiab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series (mathematics)
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures (such as in combinatorics) through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance. For a long time, the idea that such a potentially infinite summation could produce a finite result was considered paradoxical. This paradox was resolved using the concept of a limit during the 17th century. Zeno's paradox of Achilles and the tortoise illustrates this counterintuitive property of infinite sums: Achilles runs after a tortoise, but when he reaches the position of the tortoise at the beginn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Of A Polynomial
In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial's monomials (individual terms) with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. For a univariate polynomial, the degree of the polynomial is simply the highest exponent occurring in the polynomial. The term order has been used as a synonym of ''degree'' but, nowadays, may refer to several other concepts (see order of a polynomial (other)). For example, the polynomial 7x^2y^3 + 4x - 9, which can also be written as 7x^2y^3 + 4x^1y^0 - 9x^0y^0, has three terms. The first term has a degree of 5 (the sum of the powers 2 and 3), the second term has a degree of 1, and the last term has a degree of 0. Therefore, the polynomial has a degree of 5, which is the highest degree of any term. To determine the degree of a polynomial that is not in standard form, such as (x+1)^2 - (x-1)^2, one can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smooth Function
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives it has over some domain, called ''differentiability class''. At the very minimum, a function could be considered smooth if it is differentiable everywhere (hence continuous). At the other end, it might also possess derivatives of all orders in its domain, in which case it is said to be infinitely differentiable and referred to as a C-infinity function (or C^ function). Differentiability classes Differentiability class is a classification of functions according to the properties of their derivatives. It is a measure of the highest order of derivative that exists and is continuous for a function. Consider an open set U on the real line and a function f defined on U with real values. Let ''k'' be a non-negative integer. The function f is said to be of differentiability class ''C^k'' if the derivatives f',f'',\dots,f^ exist and are continuous on U. If f is k-di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |