|
Order-disorder Transition
In physics, the terms order and disorder designate the presence or absence of some symmetry or correlation in a many-particle system. In condensed matter physics, systems typically are ordered at low temperatures; upon heating, they undergo one or several phase transitions into less ordered states. Examples for such an order-disorder transition are: * the melting of ice: solid-liquid transition, loss of crystalline order; * the demagnetization of iron by heating above the Curie temperature: ferromagnetic-paramagnetic transition, loss of magnetic order. The degree of freedom that is ordered or disordered can be translational (crystalline ordering), rotational ( ferroelectric ordering), or a spin state (magnetic ordering). The order can consist either in a full crystalline space group symmetry, or in a correlation. Depending on how the correlations decay with distance, one speaks of long range order or short range order. If a disordered state is not in thermodynamic equilibrium, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
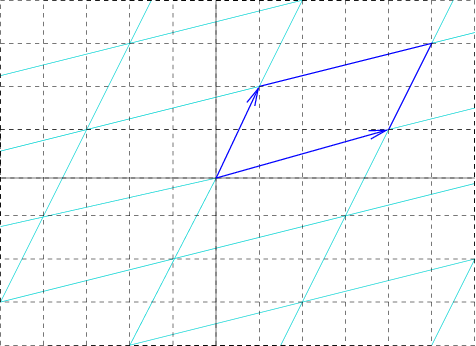
Unit Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations. There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Decay
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where is the quantity and (lambda) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant: :\frac = -\lambda N. The solution to this equation (see derivation below) is: :N(t) = N_0 e^, where is the quantity at time , is the initial quantity, that is, the quantity at time . Measuring rates of decay Mean lifetime If the decaying quantity, ''N''(''t''), is the number of discrete elements in a certain set, it is possible to compute the average length of time that an element remains in the set. This is called the mean lifetime (or simply the lifetime), where the exponential time constant, \tau, relates to the decay rate constant, λ, in the following way: :\tau = \frac. The mean lifetime can be looked at as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin (physics)
Spin is a conserved quantity carried by elementary particles, and thus by composite particles (hadrons) and atomic nucleus, atomic nuclei. Spin is one of two types of angular momentum in quantum mechanics, the other being ''orbital angular momentum''. The orbital angular momentum operator is the quantum-mechanical counterpart to the classical angular momentum of orbital revolution and appears when there is periodic structure to its wavefunction as the angle varies. For photons, spin is the quantum-mechanical counterpart of the Polarization (waves), polarization of light; for electrons, the spin has no classical counterpart. The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum. The existence of the electron spin can also be inferred theoretically from the spin–statistics theorem and from th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Function
A correlation function is a function that gives the statistical correlation between random variables, contingent on the spatial or temporal distance between those variables. If one considers the correlation function between random variables representing the same quantity measured at two different points, then this is often referred to as an autocorrelation function, which is made up of autocorrelations. Correlation functions of different random variables are sometimes called cross-correlation functions to emphasize that different variables are being considered and because they are made up of cross-correlations. Correlation functions are a useful indicator of dependencies as a function of distance in time or space, and they can be used to assess the distance required between sample points for the values to be effectively uncorrelated. In addition, they can form the basis of rules for interpolating values at points for which there are no observations. Correlation functions used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
System
A system is a group of Interaction, interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its environment (systems), environment, is described by its boundaries, structure and purpose and expressed in its functioning. Systems are the subjects of study of systems theory and other systems sciences. Systems have several common properties and characteristics, including structure, function(s), behavior and interconnectivity. Etymology The term ''system'' comes from the Latin word ''systēma'', in turn from Greek language, Greek ''systēma'': "whole concept made of several parts or members, system", literary "composition"."σύστημα" Henry George Liddell, Robert Scott, ''A Greek–English Lexicon'', on Per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (order And Disorder)
In thermodynamics, entropy is often associated with the amount of order or disorder in a thermodynamic system. This stems from Rudolf Clausius' 1862 assertion that any thermodynamic process always "admits to being reduced eductionto the alteration in some way or another of the ''arrangement'' of the constituent parts of the working body" and that internal work associated with these alterations is quantified energetically by a measure of "entropy" change, according to the following differential expression: :\int \frac \ge 0 where ''Q'' = motional energy (“heat”) that is transferred reversibly to the system from the surroundings and T = the absolute temperature at which the transfer occurs In the years to follow, Ludwig Boltzmann translated these 'alterations of arrangement' into a probabilistic view of order and disorder in gas-phase molecular systems. In the context of entropy, "''perfect internal disorder''" has often been regarded as describing thermodynamic equilibrium, b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics applies to a wide variety of topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering and mechanical engineering, but also in other complex fields such as meteorology. Historically, thermodynamics developed out of a desire to increase the efficiency of early steam engines, particularly through the work of French physicist Sadi Carnot (1824) who believed that engine efficiency was the key that could help France win the Napoleonic Wars. Scots-Irish physicist Lord Kelvin was the first to formulate a co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutron Diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material. A sample to be examined is placed in a beam of thermal or cold neutrons to obtain a diffraction pattern that provides information of the structure of the material. The technique is similar to X-ray diffraction but due to their different scattering properties, neutrons and X-rays provide complementary information: X-Rays are suited for superficial analysis, strong x-rays from synchrotron radiation are suited for shallow depths or thin specimens, while neutrons having high penetration depth are suited for bulk samples.Measurement of residual stress in materials using neutrons |
Magnetic Ordering
Magnetism is the class of physical attributes that are mediated by a magnetic field, which refers to the capacity to induce attractive and repulsive phenomena in other entities. Electric currents and the magnetic moments of elementary particles give rise to a magnetic field, which acts on other currents and magnetic moments. Magnetism is one aspect of the combined phenomena of electromagnetism. The most familiar effects occur in ferromagnetic materials, which are strongly attracted by magnetic fields and can be magnetized to become permanent magnets, producing magnetic fields themselves. Demagnetizing a magnet is also possible. Only a few substances are ferromagnetic; the most common ones are iron, cobalt, and nickel and their alloys. The rare-earth metals neodymium and samarium are less common examples. The prefix ' refers to iron because permanent magnetism was first observed in lodestone, a form of natural iron ore called magnetite, Fe3O4. All substances exhibit some type of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin (physics)
Spin is a conserved quantity carried by elementary particles, and thus by composite particles (hadrons) and atomic nucleus, atomic nuclei. Spin is one of two types of angular momentum in quantum mechanics, the other being ''orbital angular momentum''. The orbital angular momentum operator is the quantum-mechanical counterpart to the classical angular momentum of orbital revolution and appears when there is periodic structure to its wavefunction as the angle varies. For photons, spin is the quantum-mechanical counterpart of the Polarization (waves), polarization of light; for electrons, the spin has no classical counterpart. The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum. The existence of the electron spin can also be inferred theoretically from the spin–statistics theorem and from th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charge Ordering
Charge ordering (CO) is a (first- or second-order) phase transition occurring mostly in strongly correlated materials such as transition metal oxides or organic conductors. Due to the strong interaction between electrons, charges are localized on different sites leading to a disproportionation and an ordered superlattice. It appears in different patterns ranging from vertical to horizontal stripes to a checkerboard–like pattern , and it is not limited to the two-dimensional case. The charge order transition is accompanied by symmetry breaking and may lead to ferroelectricity. It is often found in close proximity to superconductivity and colossal magnetoresistance. This long range order phenomena was first discovered in magnetite (Fe3O4) by Verwey in 1939. He observed an increase of the electrical resistivity by two orders of magnitude at TCO=120K, suggesting a phase transition which is now well known as the Verwey transition. He was the first to propose the idea of an orderin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.jpg)

.gif)
