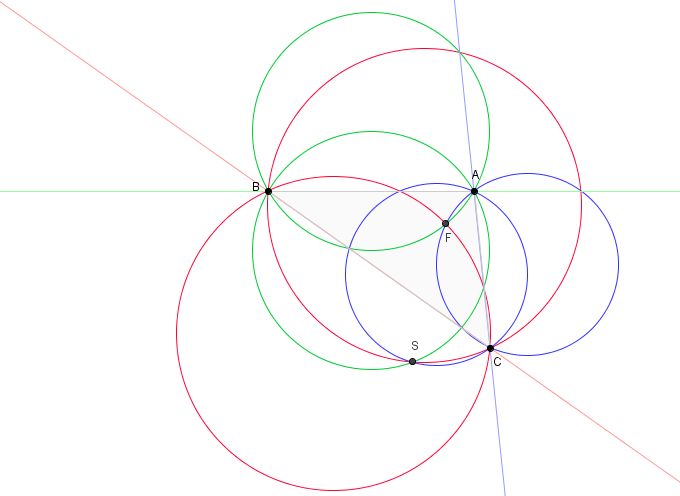
|
Orthocentroidal Disk
In geometry, the orthocentroidal circle of a non-equilateral triangle is the circle that has the triangle's orthocenter and centroid at opposite ends of its diameter. This diameter also contains the triangle's nine-point center and is a subset of the Euler line, which also contains the circumcenter outside the orthocentroidal circle. Andrew Guinand showed in 1984 that the triangle's incenter must lie in the interior of the orthocentroidal circle, but not coinciding with the nine-point center; that is, it must fall in the open orthocentroidal disk punctured at the nine-point center... . The incenter could be any such point, depending on the specific triangle having that particular orthocentroidal disk. Furthermore, the Fermat point, the Gergonne point, and the symmedian point are in the open orthocentroidal disk punctured at its own center (and could be at any point therein), while the second Fermat point and Feuerbach point are in the exterior of the orthocentroidal circle. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthocentroidal Disk
In geometry, the orthocentroidal circle of a non-equilateral triangle is the circle that has the triangle's orthocenter and centroid at opposite ends of its diameter. This diameter also contains the triangle's nine-point center and is a subset of the Euler line, which also contains the circumcenter outside the orthocentroidal circle. Andrew Guinand showed in 1984 that the triangle's incenter must lie in the interior of the orthocentroidal circle, but not coinciding with the nine-point center; that is, it must fall in the open orthocentroidal disk punctured at the nine-point center... . The incenter could be any such point, depending on the specific triangle having that particular orthocentroidal disk. Furthermore, the Fermat point, the Gergonne point, and the symmedian point are in the open orthocentroidal disk punctured at its own center (and could be at any point therein), while the second Fermat point and Feuerbach point are in the exterior of the orthocentroidal circle. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Mathematical Monthly
''The American Mathematical Monthly'' is a mathematical journal founded by Benjamin Finkel in 1894. It is published ten times each year by Taylor & Francis for the Mathematical Association of America. The ''American Mathematical Monthly'' is an expository journal intended for a wide audience of mathematicians, from undergraduate students to research professionals. Articles are chosen on the basis of their broad interest and reviewed and edited for quality of exposition as well as content. In this the ''American Mathematical Monthly'' fulfills a different role from that of typical mathematical research journals. The ''American Mathematical Monthly'' is the most widely read mathematics journal in the world according to records on JSTOR. Tables of contents with article abstracts from 1997–2010 are availablonline The MAA gives the Lester R. Ford Awards annually to "authors of articles of expository excellence" published in the ''American Mathematical Monthly''. Editors *2022– ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brocard Points
In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard (1845–1922), a French mathematician. Definition In a triangle ''ABC'' with sides ''a'', ''b'', and ''c'', where the vertices are labeled ''A'', ''B'' and ''C'' in counterclockwise order, there is exactly one point ''P'' such that the line segments ''AP'', ''BP'', and ''CP'' form the same angle, ω, with the respective sides ''c'', ''a'', and ''b'', namely that : \angle PAB = \angle PBC = \angle PCA =\omega.\, Point ''P'' is called the first Brocard point of the triangle ''ABC'', and the angle ''ω'' is called the Brocard angle of the triangle. This angle has the property that :\cot\omega = \cot \alpha + \cot \beta + \cot \gamma, \, where \alpha, \, \beta, \, \gamma are the vertex angles \angle CAB, \, \angle ABC, \, \angle BCA respectively. There is also a second Brocard point, Q, in triangle ''ABC'' such that line segments ''AQ'', ''BQ'', and ''CQ'' form equal angles wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locus (mathematics)
In geometry, a locus (plural: ''loci'') (Latin word for "place", "location") is a set of all points (commonly, a line, a line segment, a curve or a surface), whose location satisfies or is determined by one or more specified conditions.. In other words, the set of the points that satisfy some property is often called the ''locus of a point'' satisfying this property. The use of the singular in this formulation is a witness that, until the end of the 19th century, mathematicians did not consider infinite sets. Instead of viewing lines and curves as sets of points, they viewed them as places where a point may be ''located'' or may move. History and philosophy Until the beginning of the 20th century, a geometrical shape (for example a curve) was not considered as an infinite set of points; rather, it was considered as an entity on which a point may be located or on which it moves. Thus a circle in the Euclidean plane was defined as the ''locus'' of a point that is at a given dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feuerbach Point
In the geometry of triangles, the incircle and nine-point circle of a triangle are internally tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is a triangle center, meaning that its definition does not depend on the placement and scale of the triangle. It is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers, and is named after Karl Wilhelm Feuerbach..Encyclopedia of Triangle Centers , accessed 2014-10-24. Feuerbach's theorem, published by Feuerbach in 1822, states more generally that the nine-point circle is tangent to the three s of the triangle as well as its incircle. A very short proof of this theorem based on |
Symmedian Point
In geometry, symmedians are three particular lines associated with every triangle. They are constructed by taking a median of the triangle (a line connecting a vertex with the midpoint of the opposite side), and reflecting the line over the corresponding angle bisector (the line through the same vertex that divides the angle there in half). The angle formed by the symmedian and the angle bisector has the same measure as the angle between the median and the angle bisector, but it is on the other side of the angle bisector. The three symmedians meet at a triangle center called the Lemoine point. Ross Honsberger has called its existence "one of the crown jewels of modern geometry".. Isogonality Many times in geometry, if we take three special lines through the vertices of a triangle, or ''cevians'', then their reflections about the corresponding angle bisectors, called ''isogonal lines'', will also have interesting properties. For instance, if three cevians of a triangle intersect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gergonne Point
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter. An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides. The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex , for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex , or the excenter of . Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat Point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it. The Fermat point gives a solution to the geometric median and Steiner tree problems for three points. Construction The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows: # Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle. # Draw a line from each new vertex to the opposite vertex of the original triangle. # The two lines intersect at the Fermat point. An alternative method is the following: # On each of two arbitrarily chosen sides, construct an isosceles triangle, with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Gazette
''The Mathematical Gazette'' is an academic journal of mathematics education, published three times yearly, that publishes "articles about the teaching and learning of mathematics with a focus on the 15–20 age range and expositions of attractive areas of mathematics." It was established in 1894 by Edward Mann Langley as the successor to the Reports of the Association for the Improvement of Geometrical Teaching. Its publisher is the Mathematical Association. William John Greenstreet was its editor for more than thirty years (1897–1930). Since 2000, the editor is Gerry Leversha. Editors * Edward Mann Langley: 1894-1896 * Francis Sowerby Macaulay: 1896-1897 * William John Greenstreet: 1897-1930 * Alan Broadbent: 1930-1955 * Reuben Goodstein: 1956-1962 * Edwin A. Maxwell: 1962-1971 * Douglas Quadling Douglas Arthur Quadling (1926–2015) was an English mathematician, school master and educationalist who was one of the four drivers behind the School Mathematics Project (SMP) i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forum Geometricorum
''Forum Geometricorum: A Journal on Classical Euclidean Geometry'' is a peer-reviewed open-access academic journal that specializes in mathematical research papers on Euclidean geometry. It was founded in 2001, is published by Florida Atlantic University Florida Atlantic University (Florida Atlantic or FAU) is a public research university with its main campus in Boca Raton, Florida, and satellite campuses in Dania Beach, Davie, Fort Lauderdale, Jupiter, and Fort Pierce. FAU belongs to the 12-ca ..., and is indexed among others by Mathematical Reviews and . Its founding editor-in-chief was Paul Yiu, a professor of mathematics at Florida Atlantic, now retired. All papers are available online immediately upon acceptance through the journal's web site. , Forum Geometricorum is no longer accepting submissions. Prior issues are still available. See also * International Journal of Geometry References External links * {{official website, http://forumgeom.fau.edu/ Mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incenter
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle. Together with the centroid, circumcenter, and orthocenter, it is one of the four triangle centers known to the ancient Greeks, and the only one of the four that does not in general lie on the Euler line. It is the first listed center, X(1), in Clark Kimberling's Encyclopedia of Triangle Centers, and the identity element of the multiplicative group of triangle centers.. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
