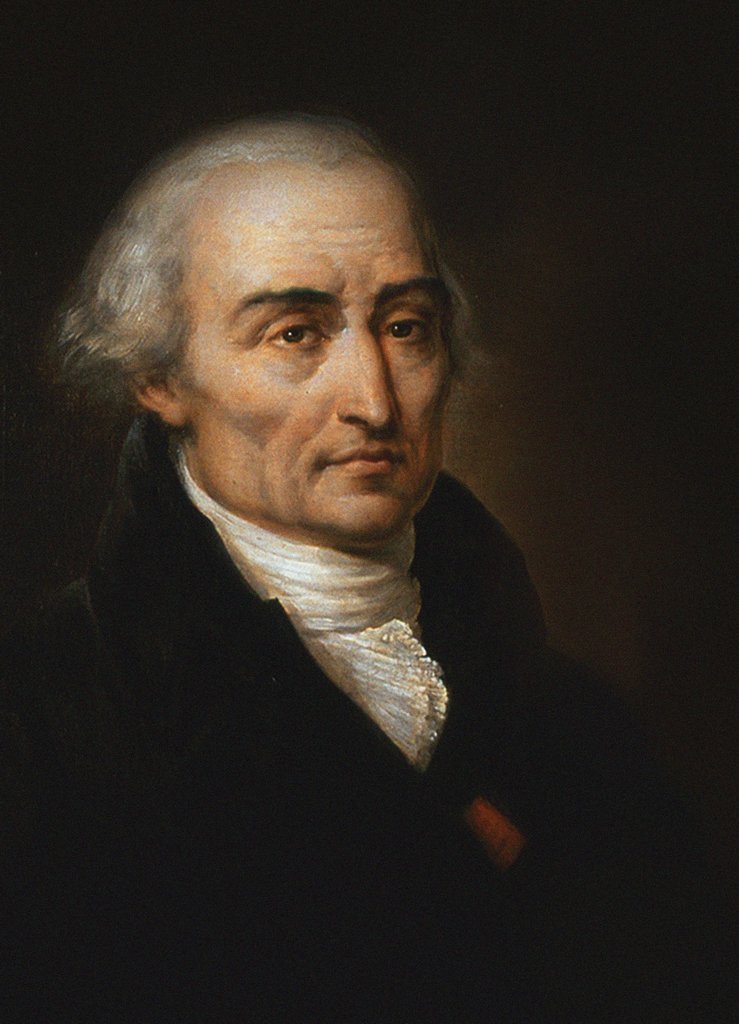|
Newton's Notation
In differential calculus, there is no single uniform notation for differentiation. Instead, various notations for the derivative of a function or variable have been proposed by various mathematicians. The usefulness of each notation varies with the context, and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation (and its opposite operation, the antidifferentiation or indefinite integration) are listed below. Leibniz's notation The original notation employed by Gottfried Leibniz is used throughout mathematics. It is particularly common when the equation is regarded as a functional relationship between dependent and independent variables and . Leibniz's notation makes this relationship explicit by writing the derivative as :\frac. Furthermore, the derivative of at is therefore written :\frac(x)\text\frac\text\frac f(x). Higher derivatives are written as :\frac, \frac, \frac, \ldots, \frac. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Calculus
In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve. The primary objects of study in differential calculus are the derivative of a function, related notions such as the differential, and their applications. The derivative of a function at a chosen input value describes the rate of change of the function near that input value. The process of finding a derivative is called differentiation. Geometrically, the derivative at a point is the slope of the tangent line to the graph of the function at that point, provided that the derivative exists and is defined at that point. For a real-valued function of a single real variable, the derivative of a function at a point generally determines the best linear approximation to the function at that point. Differential calculus and integral calcul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph Louis Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaJoseph-Louis Lagrange, comte de l’Empire ''Encyclopædia Britannica'' or Giuseppe Ludovico De la Grange Tournier; 25 January 1736 – 10 April 1813), also reported as Giuseppe Luigi Lagrange or Lagrangia, was an Italian and , later naturalized |