|
Numerical Renormalization Group
The numerical renormalization group (NRG) is a technique devised by Kenneth Wilson to solve certain many-body problems where quantum impurity physics plays a key role. History The numerical renormalization group is an inherently non-perturbative procedure, which was originally used to solve the Kondo model. The Kondo model is a simplified theoretical model which describes a system of magnetic spin-1/2 impurities which couple to metallic conduction electrons (e.g. iron impurities in gold). This problem is notoriously difficult to tackle theoretically, since perturbative techniques break down at low-energy. However, Wilson was able to prove for the first time using the numerical renormalization group that the ground state of the Kondo model is a singlet state. But perhaps more importantly, the notions of renormalization, fixed points, and renormalization group flow were introduced to the field of condensed matter theory — it is for this that Wilson won the Nobel Prize in 1982. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kenneth G
Kenneth Geoffrey Oudejans (born Amsterdam, Netherlands ), better known by his stage name Kenneth G, is a Dutch DJ and record producer. He became known in 2013 with his releases on the Dutch label Hysteria Records before joining Revealed Recordings the following year. Discography Charting singles Singles * 2008: ''Wobble'' lub Generation* 2009: ''Konichiwa Bitches!'' (with Nicky Romero) ade In NL (Spinnin')* 2010: ''Are U Serious'' elekted Music* 2011: ''Tjoppings'' ade In NL (Spinnin')* 2012: ''Bazinga'' ysteria Recs* 2012: ''Wobble'' ig Boss Records* 2013: ''Duckface'' (with Bassjackers) ysteria Recs* 2013: ''Basskikker'' nes To Watch Records (Mixmash)* 2013: ''Stay Weird'' ysteria Recs* 2013: ''Rage-Aholics'' evealed Recordings* 2014: ''RAVE-OLUTION'' (with AudioTwinz) ysteria Recs* 2014: ''97'' (with FTampa) evealed Recordings* 2014: ''Rampage'' (with Bassjackers) evealed Recordings* 2014: ''Blowfish'' (with Quintino) ly Eye Records LY or ly may refer to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
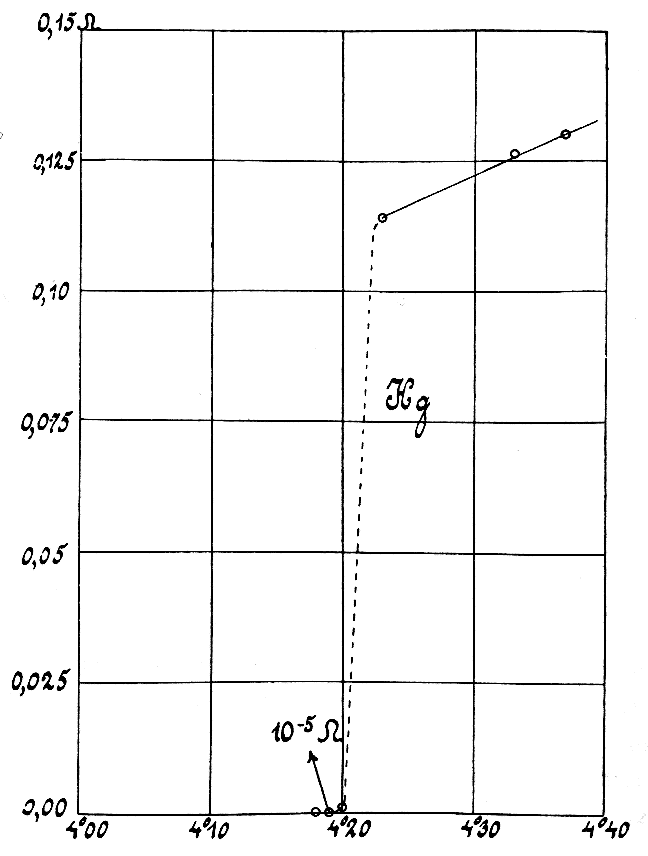
Kondo Effect
In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities, resulting in a characteristic change i.e. a minimum in electrical resistivity with temperature. The cause of the effect was first explained by Jun Kondo, who applied third-order perturbation theory to the problem to account for scattering of s-orbital conduction electrons off d-orbital electrons localized at impurities ( Kondo model). Kondo's calculation predicted that the scattering rate and the resulting part of the resistivity should increase logarithmically as the temperature approaches 0 K. Experiments in the 1960s by Myriam Sarachik at Bell Laboratories provided the first data that confirmed the Kondo effect. Extended to a lattice of ''magnetic impurities'', the Kondo effect likely explains the formation of ''heavy fermions'' and ''Kondo insulators'' in intermetallic compounds, especially those involving rare earth elements such as cerium, praseodymium, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin-1/2
In quantum mechanics, spin is an intrinsic property of all elementary particles. All known fermions, the particles that constitute ordinary matter, have a spin of . The spin number describes how many symmetrical facets a particle has in one full rotation; a spin of means that the particle must be rotated by two full turns (through 720°) before it has the same configuration as when it started. Particles having net spin include the proton, neutron, electron, neutrino, and quarks. The dynamics of spin- objects cannot be accurately described using classical physics; they are among the simplest systems which require quantum mechanics to describe them. As such, the study of the behavior of spin- systems forms a central part of quantum mechanics. Stern–Gerlach experiment The necessity of introducing half-integer spin goes back experimentally to the results of the Stern–Gerlach experiment. A beam of atoms is run through a strong heterogeneous magnetic field, which then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metal
A metal (from Greek μέταλλον ''métallon'', "mine, quarry, metal") is a material that, when freshly prepared, polished, or fractured, shows a lustrous appearance, and conducts electricity and heat relatively well. Metals are typically ductile (can be drawn into wires) and malleable (they can be hammered into thin sheets). These properties are the result of the '' metallic bond'' between the atoms or molecules of the metal. A metal may be a chemical element such as iron; an alloy such as stainless steel; or a molecular compound such as polythiazyl, polymeric sulfur nitride. In physics, a metal is generally regarded as any substance capable of conducting electricity at a temperature of absolute zero. Many elements and compounds that are not normally classified as metals become metallic under high pressures. For example, the nonmetal iodine gradually becomes a metal at a pressure of between 40 and 170 thousand times atmospheric pressure. Equally, some materials re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Renormalization
Renormalization is a collection of techniques in quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian. For example, an electron theory may begin by postulating an electron with an initial mass and charge. In quantum field theory a cloud of virtual particles, such as photons, positrons, and others surrounds and interacts with the initial electron. Accounting for the interactions of the surrounding particles (e.g. collisions at different energies) shows that the electron-system behaves as if it had a different mass and charge than initially postulated. Renormalization, in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Point (mathematics)
A fixed point (sometimes shortened to fixpoint, also known as an invariant point) is a value that does not change under a given transformation. Specifically, in mathematics, a fixed point of a function is an element that is mapped to itself by the function. In physics, the term fixed point can refer to a temperature that can be used as a reproducible reference point, usually defined by a phase change or triple point. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain and the codomain of , and . For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, , has no fixed points, since is never equal to for any real number. In graphical terms, a fixed point means the point is on the line , or in other words the graph of has a point in common with that line. Fixed-point iteration In numerical analysis, ''fixed-poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Renormalization Group
In theoretical physics, the term renormalization group (RG) refers to a formal apparatus that allows systematic investigation of the changes of a physical system as viewed at different scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle. A change in scale is called a scale transformation. The renormalization group is intimately related to ''scale invariance'' and ''conformal invariance'', symmetries in which a system appears the same at all scales (so-called self-similarity). As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation Theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In perturbation theory, the solution is expressed as a power series in a small parameter The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of \varepsilon usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, usually by keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction. Perturbation theory is used in a wide range of fields, and reaches its most sophisticated and advanced forms in quantum field theory. Perturbation theory (quantum mechanics) describes the use of this method in quantum mechanics. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resistivity
Electrical resistivity (also called specific electrical resistance or volume resistivity) is a fundamental property of a material that measures how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek letter (rho). The SI unit of electrical resistivity is the ohm- meter (Ω⋅m). For example, if a solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is , then the resistivity of the material is . Electrical conductivity or specific conductance is the reciprocal of electrical resistivity. It represents a material's ability to conduct electric current. It is commonly signified by the Greek letter (sigma), but (kappa) (especially in electrical engineering) and ( gamma) are sometimes used. The SI unit of electrical conductivity is siemens per metre (S/m). Resistivity and conductivity are int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves. The study of phonons is an important part of condensed matter physics. They play a major role in many of the physical properties of condensed matter systems, such as thermal conductivity and electrical conductivity, as well as in models of neutron scattering and related effects. The concept of phonons was introduced in 1932 by Soviet physicist Igor Tamm. The name ''phonon'' comes from the Greek word (), which translates to ''sound'' or ''voice'', because long-wavelength phonons give rise to sound. The name is analogous to the word ''photon''. Definiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anderson Impurity Model
The Anderson impurity model, named after Philip Warren Anderson, is a Hamiltonian that is used to describe magnetic impurities embedded in metals. It is often applied to the description of Kondo effect-type problems, such as heavy fermion systems and Kondo insulators. In its simplest form, the model contains a term describing the kinetic energy of the conduction electrons, a two-level term with an on-site Coulomb repulsion that models the impurity energy levels, and a hybridization term that couples conduction and impurity orbitals. For a single impurity, the Hamiltonian takes the form :H = \sum_\epsilon_k c^_c_ + \sum_\epsilon_ d^_d_ + Ud^_d_d^_d_ + \sum_V_k(d^_c_ + c^_d_), where the c operator is the annihilation operator of a conduction electron, and d is the annihilation operator for the impurity, k is the conduction electron wavevector, and \sigma labels the spin. The on–site Coulomb repulsion is U, and V gives the hybridization. Regimes The model yields several reg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.gif)