|
Non-Random Two Liquid Model
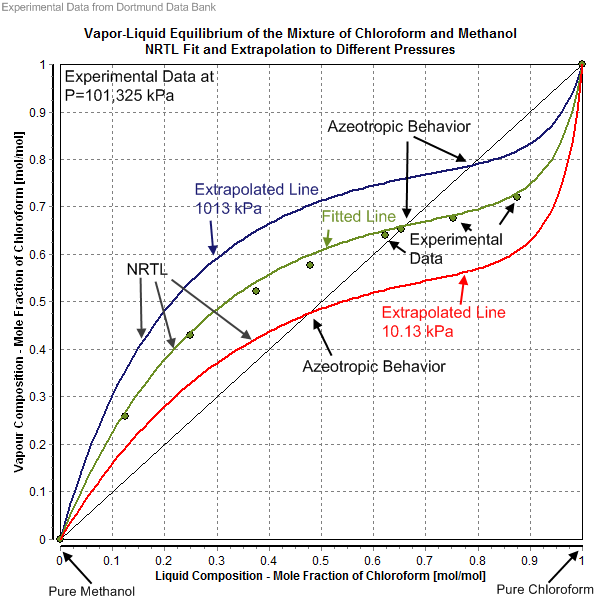
The non-random two-liquid model (abbreviated NRTL model) is an activity coefficient model that correlates the activity coefficients \gamma_i of a compound with its mole fractions x_i in the liquid phase concerned. It is frequently applied in the field of chemical engineering to calculate phase equilibria. The concept of NRTL is based on the hypothesis of Wilson that the local concentration around a molecule is different from the bulk concentration. This difference is due to a difference between the interaction energy of the central molecule with the molecules of its own kind U_ and that with the molecules of the other kind U_. The energy difference also introduces a non-randomness at the local molecular level. The NRTL model belongs to the so-called local-composition models. Other models of this type are the Wilson model, the UNIQUAC model, and the group contribution model UNIFAC. These local-composition models are not thermodynamically consistent for a one-fluid model for a real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miscibility Gap
A miscibility gap is a region in a phase diagram for a mixture of components where the mixture exists as two or more phases – any region of composition of mixtures where the constituents are not completely miscible. The IUPAC Gold Book defines ''miscibility gap'' as "Area within the coexistence curve of an isobaric phase diagram (temperature vs composition) or an isothermal phase diagram (pressure vs composition)." A miscibility gap between isostructural phases may be described as the '' solvus'', a term also used to describe the boundary on a phase diagram between a miscibility gap and other phases. Thermodynamically, miscibility gaps indicate a maximum (''e.g.'' of Gibbs energy) in the composition range. Named miscibility gaps A number of miscibility gaps in phase systems are named, including * The ''huttenlocher'' (found in bytownite Bytownite is a calcium rich member of the plagioclase solid solution series of feldspar minerals with composition between anorthite and la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Models
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics applies to a wide variety of topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering and mechanical engineering, but also in other complex fields such as meteorology. Historically, thermodynamics developed out of a desire to increase the efficiency of early steam engines, particularly through the work of French physicist Sadi Carnot (1824) who believed that engine efficiency was the key that could help France win the Napoleonic Wars. Scots-Irish physicist Lord Kelvin was the first to formulate a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Chemistry
Physical chemistry is the study of macroscopic and microscopic phenomena in chemical systems in terms of the principles, practices, and concepts of physics such as motion, energy, force, time, thermodynamics, quantum chemistry, statistical mechanics, analytical dynamics and chemical equilibria. Physical chemistry, in contrast to chemical physics, is predominantly (but not always) a supra-molecular science, as the majority of the principles on which it was founded relate to the bulk rather than the molecular or atomic structure alone (for example, chemical equilibrium and colloids). Some of the relationships that physical chemistry strives to resolve include the effects of: # Intermolecular forces that act upon the physical properties of materials ( plasticity, tensile strength, surface tension in liquids). # Reaction kinetics on the rate of a reaction. # The identity of ions and the electrical conductivity of materials. # Surface science and electrochemistry of cel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation Of State
In physics, chemistry, and thermodynamics, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate for weakly polar gases at low pressures and moderate temperatures. This equation becomes increasingly inaccurate at higher pressures and lower temperatures, and fails to predi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fugacity
In chemical thermodynamics, the fugacity of a real gas is an effective partial pressure which replaces the mechanical partial pressure in an accurate computation of the chemical equilibrium constant. It is equal to the pressure of an ideal gas which has the same temperature and molar Gibbs free energy as the real gas. Fugacities are determined experimentally or estimated from various models such as a Van der Waals gas that are closer to reality than an ideal gas. The real gas pressure and fugacity are related through the dimensionless fugacity coefficient . \varphi = \frac For an ideal gas, fugacity and pressure are equal and so . Taken at the same temperature and pressure, the difference between the molar Gibbs free energies of a real gas and the corresponding ideal gas is equal to . The fugacity is closely related to the thermodynamic activity. For a gas, the activity is simply the fugacity divided by a reference pressure to give a dimensionless quantity. This reference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
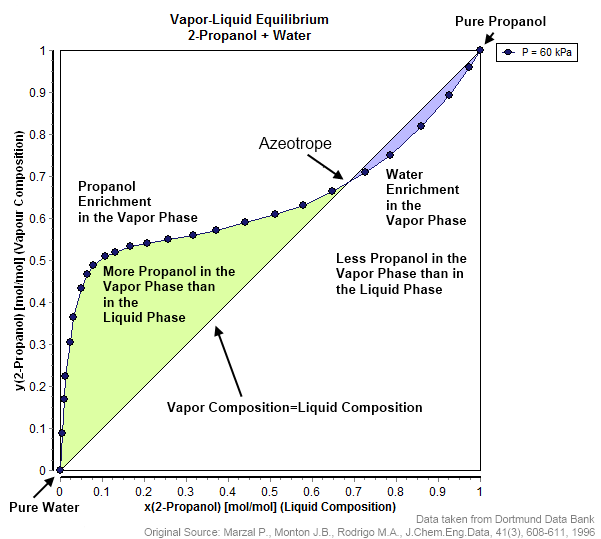
Azeotrope
An azeotrope () or a constant heating point mixture is a mixture of two or more liquids whose proportions cannot be altered or changed by simple distillation.Moore, Walter J. ''Physical Chemistry'', 3rd e Prentice-Hall 1962, pp. 140–142 This happens when an azeotrope is boiled, the vapour has the same proportions of constituents as the unboiled mixture. Because their composition is unchanged by distillation, azeotropes are also called (especially in older texts) ''constant boiling point mixtures''. Some azeotropic mixtures of pairs of compounds are known, and many azeotropes of three or more compounds are also known. In such a case it is not possible to separate the components by fractional distillation and azeotropic distillation is usually used instead. There are two types of azeotropes: minimum boiling azeotrope and maximum boiling azeotrope. A Solution (chemistry), solution that shows greater positive deviation from Raoult's law forms a minimum boiling azeotrope at a speci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
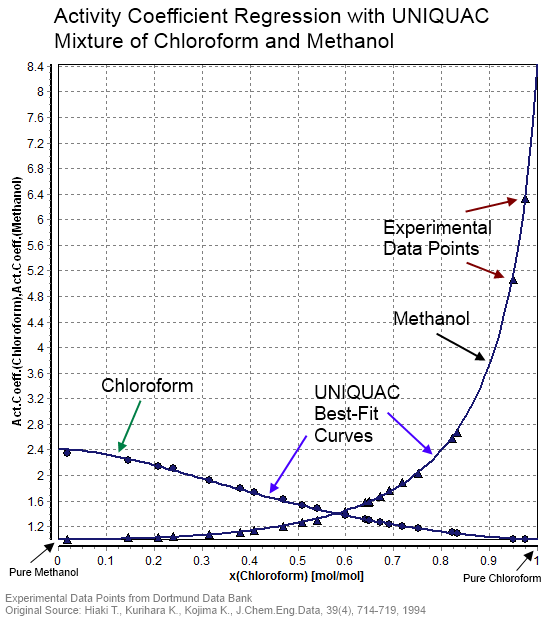
Dortmund Data Bank
The Dortmund Data Bank (short DDB) is a factual data bank for thermodynamic and thermophysical data. Its main usage is the data supply for process simulation where experimental data are the basis for the design, analysis, synthesis, and optimization of chemical processes. The DDB is used for fitting parameters for thermodynamic models like NRTL or UNIQUAC and for many different equations describing pure component properties, e.g., the Antoine equation for vapor pressures. The DDB is also used for the development and revision of predictive methods like UNIFAC and PSRK. Contents Mixture properties * Phase equilibria data ( vapor–liquid, liquid–liquid, solid–liquid), data on azeotropy and zeotropy * Mixing enthalpies * Gas solubilities * Activity coefficients at infinite dilution * Heat capacities and excess heat capacities * Volumes, densities, and excess volumes (volume effect of mixing) * Salt solubilities * Octanol-water partition coefficients * Critical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antoine Equation
The Antoine equation is a class of semi-empirical correlations describing the relation between vapor pressure and temperature for pure substances. The Antoine equation is derived from the Clausius–Clapeyron relation. The equation was presented in 1888 by the French engineer (1825–1897). Equation The Antoine equation is :\log_ p = A-\frac. where ''p'' is the vapor pressure, is temperature (in °C or in K according to the value of C) and , and are component-specific constants. The simplified form with set to zero: :\log_ p = A-\frac is the August equation, after the German physicist Ernst Ferdinand August (1795–1870). The August equation describes a linear relation between the logarithm of the pressure and the reciprocal temperature. This assumes a temperature-independent heat of vaporization. The Antoine equation allows an improved, but still inexact description of the change of the heat of vaporization with the temperature. The Antoine equation can also be transforme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Activity Coefficient
In thermodynamics, an activity coefficient is a factor used to account for deviation of a mixture of chemical substances from ideal behaviour. In an ideal mixture, the microscopic interactions between each pair of chemical species are the same (or macroscopically equivalent, the enthalpy change of solution and volume variation in mixing is zero) and, as a result, properties of the mixtures can be expressed directly in terms of simple concentrations or partial pressures of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an ''activity coefficient''. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient. The concept of activity coefficient is closely linked to that of activity in chemistry. Thermodynamic definition The chemical potential, \mu_\mathrm, of a substance B in an ideal mixture of liquids or an ideal solution is given by :\mu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margules Activity Model
The Margules activity model is a simple thermodynamic model for the excess Gibbs free energy of a liquid mixture introduced in 1895 by Max Margules. After Lewis had introduced the concept of the activity coefficient, the model could be used to derive an expression for the activity coefficients \gamma_i of a compound i in a liquid, a measure for the deviation from ideal solubility, also known as Raoult's law. In chemical engineering the Margules Gibbs free energy model for liquid mixtures is better known as the Margules activity or activity coefficient model. Although the model is old it has the characteristic feature to describe extrema in the activity coefficient, which modern models like NRTL and Wilson cannot. Equations Excess Gibbs free energy Margules expressed the intensive excess Gibbs free energy of a binary liquid mixture as a power series of the mole fractions xi: : \frac=X_1 X_2 (A_ X_1 +A_ X_2) + X_1^2 X_2^2 (B_X_1+ B_ X_2) + ... + X_1^m X_2^m (M_X_1+ M_ X_2) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gas Constant
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, i.e. the pressure–volume product, rather than energy per temperature increment per ''particle''. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation. The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |