|
Neumann Series
A Neumann series is a mathematical series of the form : \sum_^\infty T^k where T is an operator and T^k := T^\circ its k times repeated application. This generalizes the geometric series. The series is named after the mathematician Carl Neumann, who used it in 1877 in the context of potential theory. The Neumann series is used in functional analysis. It forms the basis of the Liouville-Neumann series, which is used to solve Fredholm integral equations. It is also important when studying the spectrum of bounded operators. Properties Suppose that T is a bounded linear operator on the normed vector space X. If the Neumann series converges in the operator norm, then \text-T is invertible and its inverse is the series: : (\mathrm - T)^ = \sum_^\infty T^k , where \mathrm is the identity operator in X. To see why, consider the partial sums :S_n := \sum_^n T^k. Then we have :\lim_(\mathrm-T)S_n = \lim_\left(\sum_^n T^k - \sum_^n T^\right) = \lim_\left(\mathrm - T^\right) = \math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series (mathematics)
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures (such as in combinatorics) through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance. For a long time, the idea that such a potentially infinite summation could produce a finite result was considered paradoxical. This paradox was resolved using the concept of a limit during the 17th century. Zeno's paradox of Achilles and the tortoise illustrates this counterintuitive property of infinite sums: Achilles runs after a tortoise, but when he reaches the position of the tortoise at the beginning of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergent Series
In mathematics, a series is the sum of the terms of an infinite sequence of numbers. More precisely, an infinite sequence (a_0, a_1, a_2, \ldots) defines a series that is denoted :S=a_0 +a_1+ a_2 + \cdots=\sum_^\infty a_k. The th partial sum is the sum of the first terms of the sequence; that is, :S_n = \sum_^n a_k. A series is convergent (or converges) if the sequence (S_1, S_2, S_3, \dots) of its partial sums tends to a limit; that means that, when adding one a_k after the other ''in the order given by the indices'', one gets partial sums that become closer and closer to a given number. More precisely, a series converges, if there exists a number \ell such that for every arbitrarily small positive number \varepsilon, there is a (sufficiently large) integer N such that for all n \ge N, :\left , S_n - \ell \right , 1 produce a convergent series: *: ++++++\cdots = . * Alternating the signs of reciprocals of powers of 2 also produces a convergent series: *: -+-+-+\cdots = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
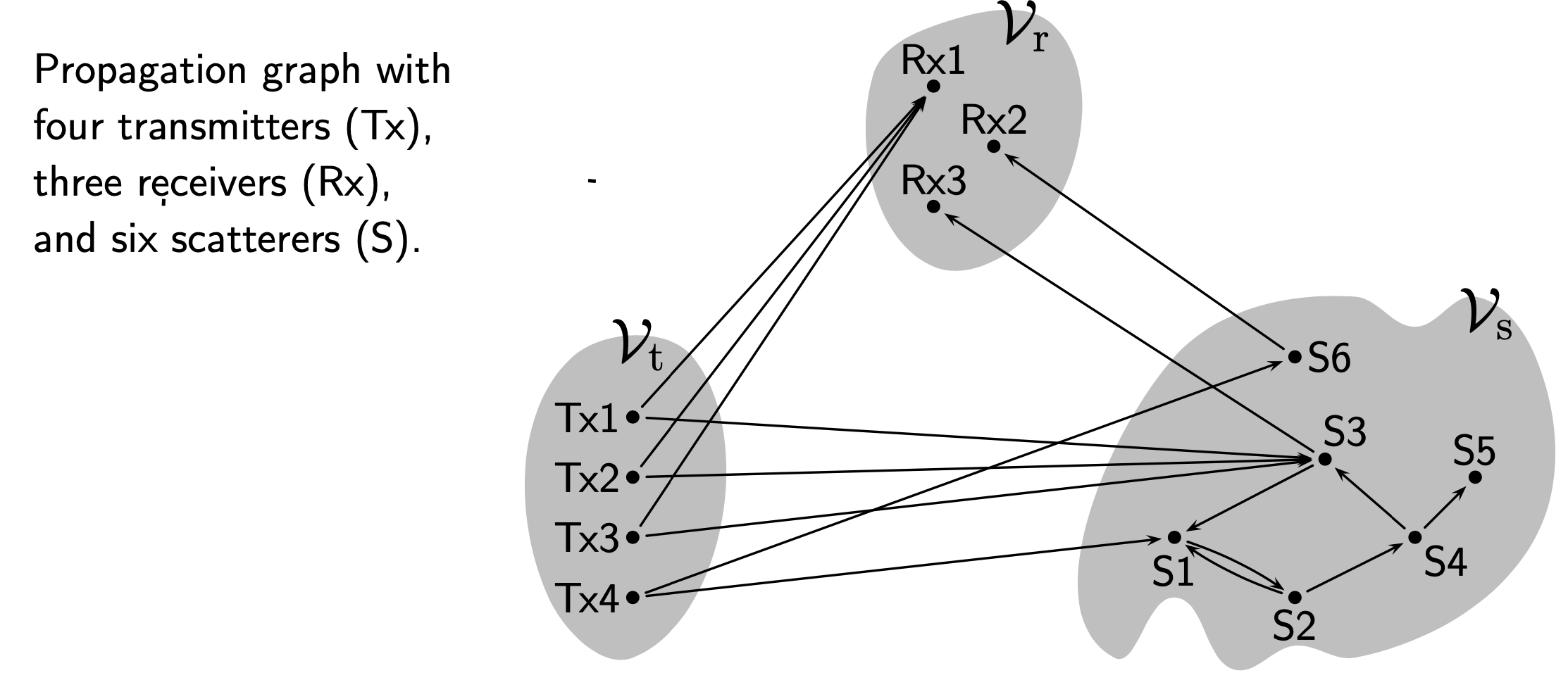
Propagation Graph
Propagation graphs are a mathematical modelling method for radio propagation channels. A propagation graph is a signal flow graph in which vertices represent transmitters, receivers or scatterers. Edges in the graph model propagation conditions between vertices. Propagation graph models were initially developed by Troels Pedersen, et al. for multipath propagation in scenarios with multiple scattering, such as indoor radio propagation. It has later been applied in many other scenarios. Mathematical definition A propagation graph is a simple directed graph \mathcal G = (\mathcal V, \mathcal E) with vertex set \mathcal V and edge set \mathcal E. The vertices models objects in the propagation scenario. The vertex set \mathcal V is split into three disjoint sets as \mathcal V = \mathcal V_t \cup \mathcal V_r \cup\mathcal V_s where \mathcal V_t is the set of transmitters, \mathcal V_r is the set of receivers and \mathcal V_s is the set of objects named "scatterers". The ed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invertible Matrix
In linear algebra, an -by- square matrix is called invertible (also nonsingular or nondegenerate), if there exists an -by- square matrix such that :\mathbf = \mathbf = \mathbf_n \ where denotes the -by- identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix is uniquely determined by , and is called the (multiplicative) ''inverse'' of , denoted by . Matrix inversion is the process of finding the matrix that satisfies the prior equation for a given invertible matrix . A square matrix that is ''not'' invertible is called singular or degenerate. A square matrix is singular if and only if its determinant is zero. Singular matrices are rare in the sense that if a square matrix's entries are randomly selected from any finite region on the number line or complex plane, the probability that the matrix is singular is 0, that is, it will "almost never" be singular. Non-square matrices (-by- matrices for which ) do not hav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Norm
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices (of given dimensions). Preliminaries Given a field K of either real or complex numbers, let K^ be the -vector space of matrices with m rows and n columns and entries in the field K. A matrix norm is a norm on K^. This article will always write such norms with double vertical bars (like so: \, A\, ). Thus, the matrix norm is a function \, \cdot\, : K^ \to \R that must satisfy the following properties: For all scalars \alpha \in K and matrices A, B \in K^, *\, A\, \ge 0 (''positive-valued'') *\, A\, = 0 \iff A=0_ (''definite'') *\left\, \alpha A\right\, =\left, \alpha\ \left\, A\right\, (''absolutely homogeneous'') *\, A+B\, \le \, A\, +\, B\, (''sub-additive'' or satisfying the ''triangle inequality'') The only feature distinguishing matrices from rearranged vectors is multiplication. Matrix norms are particularly useful if they are also sub-multiplicative: *\left\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach Space
In mathematics, more specifically in functional analysis, a Banach space (pronounced ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space. Banach spaces are named after the Polish mathematician Stefan Banach, who introduced this concept and studied it systematically in 1920–1922 along with Hans Hahn and Eduard Helly. Maurice René Fréchet was the first to use the term "Banach space" and Banach in turn then coined the term "Fréchet space." Banach spaces originally grew out of the study of function spaces by Hilbert, Fréchet, and Riesz earlier in the century. Banach spaces play a central role in functional analysis. In other areas of analysis, the spaces under study are often Banach spaces. Definition A Banach space is a complete norme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Operator
Identity may refer to: * Identity document * Identity (philosophy) * Identity (social science) * Identity (mathematics) Arts and entertainment Film and television * ''Identity'' (1987 film), an Iranian film * ''Identity'' (2003 film), an American slasher film * ''Identity'' (game show), an American game show * ''Identity'' (TV series), a British police procedural drama television series * "Identity" (''Arrow''), a 2013 episode * "Identity" (''Burn Notice''), a 2007 episode * "Identity" (''Charlie Jade''), a 2005 episode * "Identity" (''Legend of the Seeker''), a 2008 episode * "Identity" (''Law & Order: Special Victims Unit'' episode), 2005 * "Identity" (''NCIS: Los Angeles''), a 2009 pilot episode Music Albums * ''Identity'' (3T album), 2004 * ''Identity'' (BoA album), 2010 * ''Identity'' (Far East Movement album), 2016 * ''Identity'' (Robert Pierre album), 2008 * ''Identity'' (Raghav album), 2008 * ''Identity'' (Victon EP), 2017 * ''Identity'' (Zee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invertible Matrix
In linear algebra, an -by- square matrix is called invertible (also nonsingular or nondegenerate), if there exists an -by- square matrix such that :\mathbf = \mathbf = \mathbf_n \ where denotes the -by- identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix is uniquely determined by , and is called the (multiplicative) ''inverse'' of , denoted by . Matrix inversion is the process of finding the matrix that satisfies the prior equation for a given invertible matrix . A square matrix that is ''not'' invertible is called singular or degenerate. A square matrix is singular if and only if its determinant is zero. Singular matrices are rare in the sense that if a square matrix's entries are randomly selected from any finite region on the number line or complex plane, the probability that the matrix is singular is 0, that is, it will "almost never" be singular. Non-square matrices (-by- matrices for which ) do not hav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operator Norm
In mathematics, the operator norm measures the "size" of certain linear operators by assigning each a real number called its . Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces. Introduction and definition Given two normed vector spaces V and W (over the same base field, either the real numbers \R or the complex numbers \Complex), a linear map A : V \to W is continuous if and only if there exists a real number c such that \, Av\, \leq c \, v\, \quad \mbox v\in V. The norm on the left is the one in W and the norm on the right is the one in V. Intuitively, the continuous operator A never increases the length of any vector by more than a factor of c. Thus the image of a bounded set under a continuous operator is also bounded. Because of this property, the continuous linear operators are also known as bounded operators. In order to "measure the size" of A, one can take the infimum of the numbers c such that the above i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normed Vector Space
In mathematics, a normed vector space or normed space is a vector space over the real or complex numbers, on which a norm is defined. A norm is the formalization and the generalization to real vector spaces of the intuitive notion of "length" in the real (physical) world. A norm is a real-valued function defined on the vector space that is commonly denoted x\mapsto \, x\, , and has the following properties: #It is nonnegative, meaning that \, x\, \geq 0 for every vector x. #It is positive on nonzero vectors, that is, \, x\, = 0 \text x = 0. # For every vector x, and every scalar \alpha, \, \alpha x\, = , \alpha, \, \, x\, . # The triangle inequality holds; that is, for every vectors x and y, \, x+y\, \leq \, x\, + \, y\, . A norm induces a distance, called its , by the formula d(x,y) = \, y-x\, . which makes any normed vector space into a metric space and a topological vector space. If this metric space is complete then the normed space is a Banach space. Every normed vec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operator (mathematics)
In mathematics, an operator is generally a mapping or function that acts on elements of a space to produce elements of another space (possibly and sometimes required to be the same space). There is no general definition of an ''operator'', but the term is often used in place of ''function'' when the domain is a set of functions or other structured objects. Also, the domain of an operator is often difficult to be explicitly characterized (for example in the case of an integral operator), and may be extended to related objects (an operator that acts on functions may act also on differential equations whose solutions are functions that satisfy the equation). See Operator (physics) for other examples. The most basic operators are linear maps, which act on vector spaces. Linear operators refer to linear maps whose domain and range are the same space, for example \R^n to \R^n. Such operators often preserve properties, such as continuity. For example, differentiation and indef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectrum (functional Analysis)
In mathematics, particularly in functional analysis, the spectrum of a bounded linear operator (or, more generally, an unbounded linear operator) is a generalisation of the set of eigenvalues of a matrix. Specifically, a complex number \lambda is said to be in the spectrum of a bounded linear operator T if T-\lambda I is not invertible, where I is the identity operator. The study of spectra and related properties is known as spectral theory, which has numerous applications, most notably the mathematical formulation of quantum mechanics. The spectrum of an operator on a finite-dimensional vector space is precisely the set of eigenvalues. However an operator on an infinite-dimensional space may have additional elements in its spectrum, and may have no eigenvalues. For example, consider the right shift operator ''R'' on the Hilbert space ℓ2, :(x_1, x_2, \dots) \mapsto (0, x_1, x_2, \dots). This has no eigenvalues, since if ''Rx''=''λx'' then by expanding this expression we see ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |