|
Models Of Computation
In computer science, and more specifically in computability theory and computational complexity theory, a model of computation is a model which describes how an output of a mathematical function is computed given an input. A model describes how units of computations, memories, and communications are organized. The computational complexity of an algorithm can be measured given a model of computation. Using a model allows studying the performance of algorithms independently of the variations that are specific to particular implementations and specific technology. Models Models of computation can be classified into three categories: sequential models, functional models, and concurrent models. Sequential models Sequential models include: * Finite state machines * Post machines ( Post–Turing machines and tag machines). * Pushdown automata * Register machines ** Random-access machines * Turing machines * Decision tree model Functional models Functional models include: * Abs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (including the design and implementation of hardware and software). Computer science is generally considered an area of academic research and distinct from computer programming. Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and for preventing security vulnerabilities. Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of repositories ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Recursive Function
In mathematical logic and computer science, a general recursive function, partial recursive function, or μ-recursive function is a partial function from natural numbers to natural numbers that is "computable" in an intuitive sense – as well as in a formal one. If the function is total, it is also called a total recursive function (sometimes shortened to recursive function). In computability theory, it is shown that the μ-recursive functions are precisely the functions that can be computed by Turing machines (this is one of the theorems that supports the Church–Turing thesis). The μ-recursive functions are closely related to primitive recursive functions, and their inductive definition (below) builds upon that of the primitive recursive functions. However, not every total recursive function is a primitive recursive function—the most famous example is the Ackermann function. Other equivalent classes of functions are the functions of lambda calculus and the functions tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random-access Machine
In computer science, random-access machine (RAM) is an abstract machine in the general class of register machines. The RAM is very similar to the counter machine but with the added capability of 'indirect addressing' of its registers. Like the counter machine, The RAM has its instructions in the finite-state portion of the machine (the so-called Harvard architecture). The RAM's equivalent of the universal Turing machinewith its program in the registers as well as its datais called the random-access stored-program machine or RASP. It is an example of the so-called von Neumann architecture and is closest to the common notion of a computer. Together with the Turing machine and counter-machine models, the RAM and RASP models are used for computational complexity analysis. Van Emde Boas (1990) calls these three plus the pointer machine "sequential machine" models, to distinguish them from "parallel random-access machine" models. Introduction to the model The concept of a random ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Algorithms
In computer science, the analysis of algorithms is the process of finding the computational complexity of algorithms—the amount of time, storage, or other resources needed to execute them. Usually, this involves determining a function that relates the size of an algorithm's input to the number of steps it takes (its time complexity) or the number of storage locations it uses (its space complexity). An algorithm is said to be efficient when this function's values are small, or grow slowly compared to a growth in the size of the input. Different inputs of the same size may cause the algorithm to have different behavior, so best, worst and average case descriptions might all be of practical interest. When not otherwise specified, the function describing the performance of an algorithm is usually an upper bound, determined from the worst case inputs to the algorithm. The term "analysis of algorithms" was coined by Donald Knuth. Algorithm analysis is an important part of a broad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nondeterministic Model Of Computation
In theoretical computer science, a nondeterministic Turing machine (NTM) is a theoretical model of computation whose governing rules specify more than one possible action when in some given situations. That is, an NTM's next state is ''not'' completely determined by its action and the current symbol it sees, unlike a deterministic Turing machine. NTMs are sometimes used in thought experiments to examine the abilities and limits of computers. One of the most important open problems in theoretical computer science is the P versus NP problem, which (among other equivalent formulations) concerns the question of how difficult it is to simulate nondeterministic computation with a deterministic computer. Background In essence, a Turing machine is imagined to be a simple computer that reads and writes symbols one at a time on an endless tape by strictly following a set of rules. It determines what action it should perform next according to its internal ''state'' and ''what symbol it curr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deterministic Model
In mathematics, computer science and physics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state. at Scholarpedia In physics Physical laws that are described by represent deterministic systems, even though the state of the system at a given point in time may be difficult to describe explicitly. In |
Synchronous Data Flow
Synchronous Data Flow (SDF) is a restriction on Kahn process networks where the number of tokens read and written by each process is known ahead of time. In some cases, processes can be scheduled such that channels have bounded FIFOs. Limitations SDF does not account for asynchronous processes as their token read/write rates will vary. Practically, one can divide the network into synchronous sub-networks connected by asynchronous links. Alternatively a runtime supervisor can enforce fairness and other desired properties. Applications SDF is useful for modeling digital signal processing (DSP) routines. Models can be compiled to target parallel hardware like FPGAs, processors with DSP instruction sets like Qualcomm's Hexagon, and other systems. See also *Kahn process networks *Petri net *Dataflow architecture Dataflow architecture is a dataflow-based computer architecture that directly contrasts the traditional von Neumann architecture or control flow architecture. Dataflo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
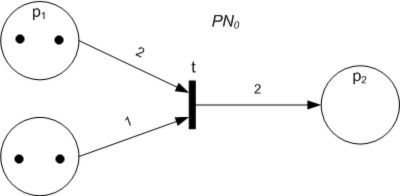
Petri Nets
A Petri net, also known as a place/transition (PT) net, is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements, places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri—at the age of 13—for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Petri net ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circuit (computer Science)
In theoretical computer science, a circuit is a model of computation in which input values proceed through a sequence of gates, each of which computes a function. Circuits of this kind provide a generalization of Boolean circuits and a mathematical model for digital logic circuits. Circuits are defined by the gates they contain and the values the gates can produce. For example, the values in a Boolean circuit are boolean values, and the circuit includes conjunction, disjunction, and negation gates. The values in an integer circuit are sets of integers and the gates compute set union, set intersection, and set complement, as well as the arithmetic operations addition and multiplication. Formal definition A circuit is a triple (M, L, G), where * M is a set of values, * L is a set of gate labels, each of which is a function from M^ to M for some non-negative integer i (where i represents the number of inputs to the gate), and * G is a labelled directed acyclic graph with labels ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic Gate
A logic gate is an idealized or physical device implementing a Boolean function, a logical operation performed on one or more binary inputs that produces a single binary output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and unlimited fan-out, or it may refer to a non-ideal physical device (see Ideal and real op-amps for comparison). Logic gates are primarily implemented using diodes or transistors acting as electronic switches, but can also be constructed using vacuum tubes, electromagnetic relays ( relay logic), fluidic logic, pneumatic logic, optics, molecules, or even mechanical elements. Now, most logic gates are made from MOSFETs (metal–oxide–semiconductor field-effect transistors). With amplification, logic gates can be cascaded in the same way that Boolean functions can be composed, allowing the construction of a physical model of all of Boolean logic, and therefore, all of the algorithms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kahn Process Networks
A Kahn process network (KPN, or process network) is a distributed ''model of computation'' in which a group of deterministic sequential processes communicate through unbounded first in, first out channels. The model requires that reading from a channel is blocking while writing is non-blocking. Due to these key restrictions, the resulting process network exhibits deterministic behavior that does not depend on the timing of computation nor on communication delays. Kahn process networks were originally developed for modeling parallel programs, but have proven convenient for modeling embedded systems, high-performance computing systems, signal processing systems, stream processing systems, dataflow programming languages, and other computational tasks. KPNs were introduced by Gilles Kahn in 1974. Execution model KPN is a common model for describing signal processing systems where infinite streams of data are incrementally transformed by processes executing in sequence or paral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
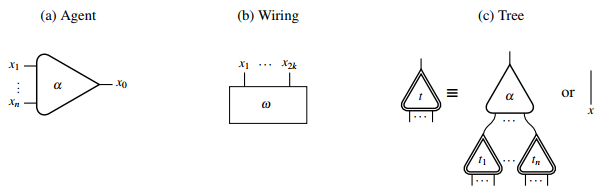
Interaction Nets
Interaction nets are a graphical model of computation devised by Yves Lafont in 1990 as a generalisation of the proof structures of linear logic. An interaction net system is specified by a set of agent types and a set of interaction rules. Interaction nets are an inherently distributed model of computation in the sense that computations can take place simultaneously in many parts of an interaction net, and no synchronisation is needed. The latter is guaranteed by the strong confluence property of reduction in this model of computation. Thus interaction nets provide a natural language for massive parallelism. Interaction nets are at the heart of many implementations of the lambda calculus, such as efficient closed reduction and optimal, in Lévy's sense, Lambdascope. Definitions Interactions nets are graph-like structures consisting of ''agents'' and ''edges''. An agent of type \alpha and with ''arity'' \text(\alpha) = n \ge 0 has one ''principal port'' and n ''auxiliary ports'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |