|
Mixed Quantum State
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in time exhausts all that can be predicted about the system's behavior. A mixture of quantum states is again a quantum state. Quantum states that cannot be written as a mixture of other states are called pure quantum states, while all other states are called mixed quantum states. A pure quantum state can be represented by a ray in a Hilbert space over the complex numbers, while mixed states are represented by density matrices, which are positive semidefinite operators that act on Hilbert spaces. Pure states are also known as state vectors or wave functions, the latter term applying particularly when they are represented as functions of position or momentum. For example, when dealing with the energy spectrum of the electron in a hydrog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Physics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
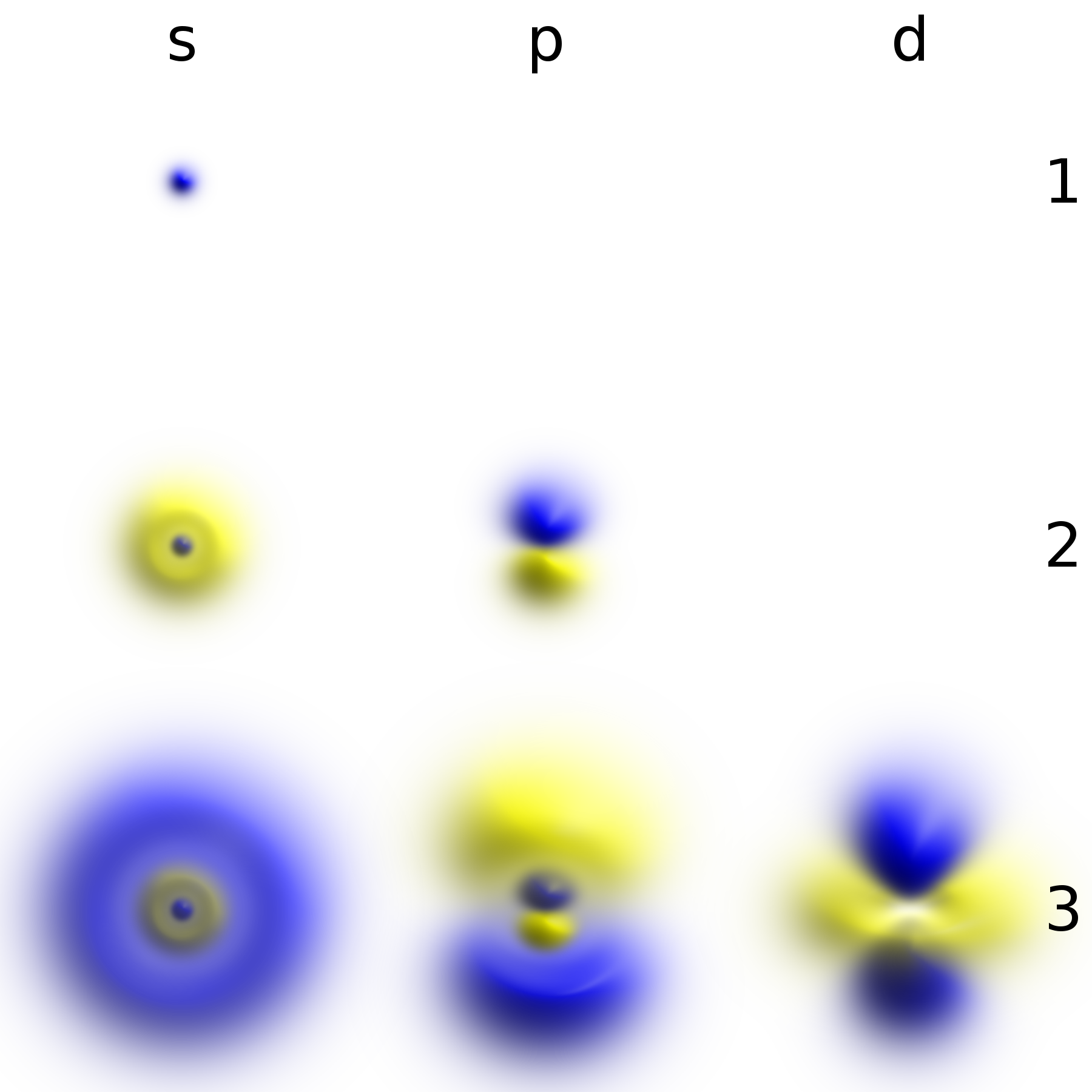
Magnetic Quantum Number
In atomic physics, the magnetic quantum number () is one of the four quantum numbers (the other three being the principal, azimuthal, and spin) which describe the unique quantum state of an electron. The magnetic quantum number distinguishes the orbitals available within a subshell, and is used to calculate the azimuthal component of the orientation of orbital in space. Electrons in a particular subshell (such as s, p, d, or f) are defined by values of (0, 1, 2, or 3). The value of can range from to , including zero. Thus the s, p, d, and f subshells contain 1, 3, 5, and 7 orbitals each, with values of within the ranges 0, ±1, ±2, ±3 respectively. Each of these orbitals can accommodate up to two electrons (with opposite spins), forming the basis of the periodic table. Derivation There is a set of quantum numbers associated with the energy states of the atom. The four quantum numbers n, \ell, m_\ell, and s specify the complete quantum state of a single electron in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Foundations Of Physics Letters
''Foundations of Physics'' is a monthly journal "devoted to the conceptual bases and fundamental theories of modern physics and cosmology, emphasizing the logical, methodological, and philosophical premises of modern physical theories and procedures". The journal publishes results and observations based on fundamental questions from all fields of physics, including: quantum mechanics, quantum field theory, special relativity, general relativity, string theory, M-theory, cosmology, thermodynamics, statistical physics, and quantum gravity ''Foundations of Physics'' has been published since 1970. Its founding editors were Henry Margenau and Wolfgang Yourgrau. The 1999 Nobel laureate Gerard 't Hooft was editor-in-chief from January 2007. At that stage, it absorbed the associated journal for shorter submissions ''Foundations of Physics Letters'', which had been edited by Alwyn Van der Merwe since its foundation in 1988. Past editorial board members (which include several Nobel laureate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
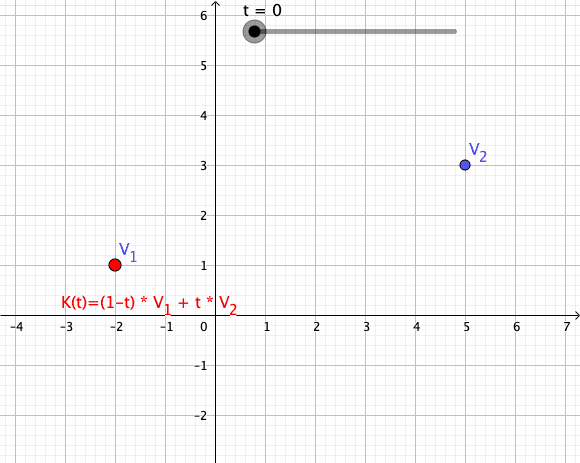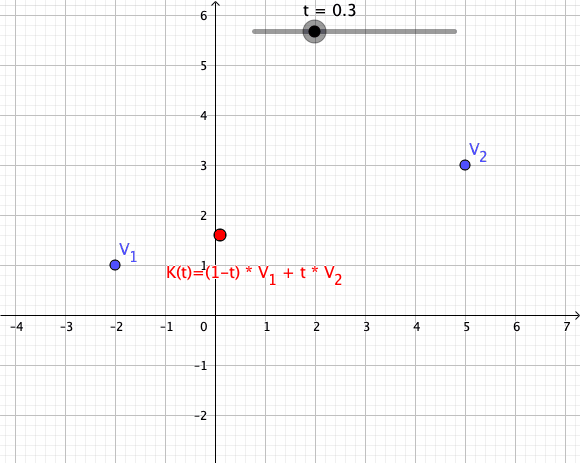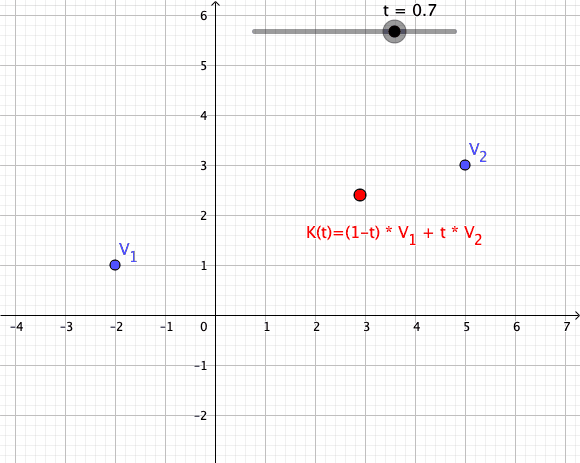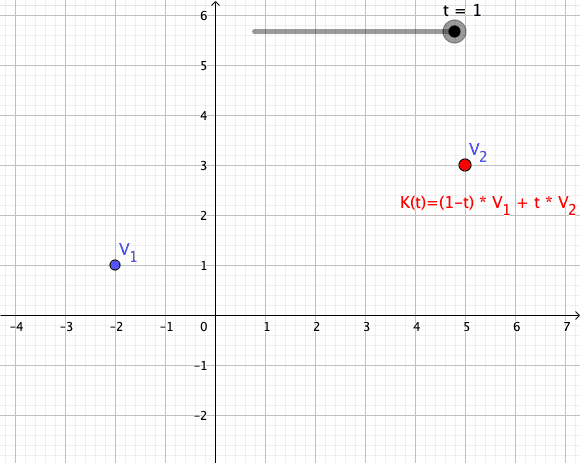
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schrödinger–HJW Theorem
In quantum information theory and quantum optics, the Schrödinger–HJW theorem is a result about the realization of a mixed state of a quantum system as an ensemble of pure quantum states and the relation between the corresponding purifications of the density operators. The theorem is named after physicists and mathematicians Erwin Schrödinger, Lane P. Hughston, Richard Jozsa and William Wootters. The result was also found independently (albeit partially) by Nicolas Gisin, and by Nicolas Hadjisavvas building upon work by Ed Jaynes, while a significant part of it was likewise independently discovered by N. David Mermin. Thanks to its complicated history, it is also known by various other names such as the GHJW theorem, the HJW theorem, and the purification theorem. Purification of a mixed quantum state Let \mathcal H_S be a finite-dimensional Hilbert space, and consider a generic (possibly mixed) quantum state \rho defined on \mathcal H_S, and admitting a decomposition of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Superposition
Quantum superposition is a fundamental principle of quantum mechanics. It states that, much like waves in classical physics, any two (or more) quantum states can be added together ("superposed") and the result will be another valid quantum state; and conversely, that every quantum state can be represented as a sum of two or more other distinct states. Mathematically, it refers to a property of solutions to the Schrödinger equation; since the Schrödinger equation is linear, any linear combination of solutions will also be a solution(s) . An example of a physically observable manifestation of the wave nature of quantum systems is the interference peaks from an electron beam in a double-slit experiment. The pattern is very similar to the one obtained by diffraction of classical waves. Another example is a quantum logical qubit state, as used in quantum information processing, which is a quantum superposition of the "basis states" , 0 \rangle and , 1 \rangle . Here , 0 \r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Entanglement
Quantum entanglement is the phenomenon that occurs when a group of particles are generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics. Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior gives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singlet State
In quantum mechanics, a singlet state usually refers to a system in which all electrons are paired. The term 'singlet' originally meant a linked set of particles whose net angular momentum is zero, that is, whose overall spin quantum number s=0. As a result, there is only one spectral line of a singlet state. In contrast, a doublet state contains one unpaired electron and shows splitting of spectral lines into a doublet; and a triplet state has two unpaired electrons and shows threefold splitting of spectral lines. History Singlets and the related spin concepts of doublets and triplets occur frequently in atomic physics and nuclear physics, where one often needs to determine the total spin of a collection of particles. Since the only observed fundamental particle with zero spin is the extremely inaccessible Higgs boson, singlets in everyday physics are necessarily composed of sets of particles whose individual spins are non-zero, e.g. or 1. The origin of the term "singlet" is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bra–ket Notation
In quantum mechanics, bra–ket notation, or Dirac notation, is used ubiquitously to denote quantum states. The notation uses angle brackets, and , and a vertical bar , to construct "bras" and "kets". A ket is of the form , v \rangle. Mathematically it denotes a vector, \boldsymbol v, in an abstract (complex) vector space V, and physically it represents a state of some quantum system. A bra is of the form \langle f, . Mathematically it denotes a linear form f:V \to \Complex, i.e. a linear map that maps each vector in V to a number in the complex plane \Complex. Letting the linear functional \langle f, act on a vector , v\rangle is written as \langle f , v\rangle \in \Complex. Assume that on V there exists an inner product (\cdot,\cdot) with antilinear first argument, which makes V an inner product space. Then with this inner product each vector \boldsymbol \phi \equiv , \phi\rangle can be identified with a corresponding linear form, by placing the vector in the anti-line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace (linear Algebra)
In linear algebra, the trace of a square matrix , denoted , is defined to be the sum of elements on the main diagonal (from the upper left to the lower right) of . The trace is only defined for a square matrix (). It can be proved that the trace of a matrix is the sum of its (complex) eigenvalues (counted with multiplicities). It can also be proved that for any two matrices and . This implies that similar matrices have the same trace. As a consequence one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the th row and th column of . The entries of can be real numbers or (more generally) complex numbers. The trace is not de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermitian Matrix
In mathematics, a Hermitian matrix (or self-adjoint matrix) is a complex square matrix that is equal to its own conjugate transpose—that is, the element in the -th row and -th column is equal to the complex conjugate of the element in the -th row and -th column, for all indices and : or in matrix form: A \text \quad \iff \quad A = \overline . Hermitian matrices can be understood as the complex extension of real symmetric matrices. If the conjugate transpose of a matrix A is denoted by A^\mathsf, then the Hermitian property can be written concisely as Hermitian matrices are named after Charles Hermite, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of always having real eigenvalues. Other, equivalent notations in common use are A^\mathsf = A^\dagger = A^\ast, although note that in quantum mechanics, A^\ast typically means the complex conjugate only, and not the conjugate transpose. Alternative characterizations Hermit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |