|
Mixed-design Analysis Of Variance
In statistics, a mixed-design analysis of variance model, also known as a split-plot ANOVA, is used to test for differences between two or more independent groups whilst subjecting participants to repeated measures. Thus, in a mixed-design ANOVA model, one factor (a fixed effects factor) is a between-subjects variable and the other (a random effects factor) is a within-subjects variable. Thus, overall, the model is a type of mixed-effects model. A repeated measures design is used when multiple independent variables or measures exist in a data set, but all participants have been measured on each variable.Field, A. (2009). Discovering Statistics Using SPSS (3rd edition). Los Angeles: Sage. An example Andy Field (2009) provided an example of a mixed-design ANOVA in which he wants to investigate whether personality or attractiveness is the most important quality for individuals seeking a partner. In his example, there is a speed dating event set up in which there are two sets ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
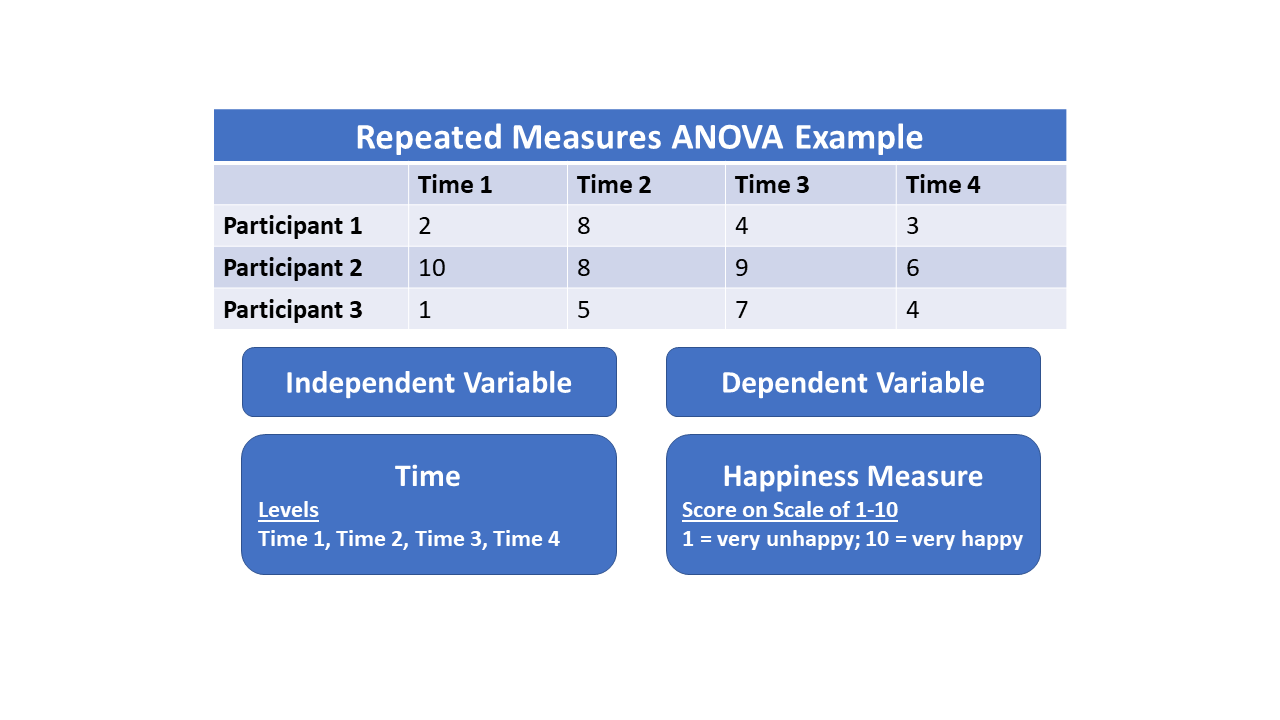
Repeated Measures
Repeated measures design is a research design that involves multiple measures of the same variable taken on the same or matched subjects either under different conditions or over two or more time periods. For instance, repeated measurements are collected in a longitudinal study in which change over time is assessed. Crossover studies A popular repeated-measures design is the crossover study. A crossover study is a longitudinal study in which subjects receive a sequence of different treatments (or exposures). While crossover studies can be observational studies, many important crossover studies are controlled experiments. Crossover designs are common for experiments in many scientific disciplines, for example psychology, education, pharmaceutical science, and health care, especially medicine. Randomized, controlled, crossover experiments are especially important in health care. In a randomized clinical trial, the subjects are randomly assigned treatments. When such a trial is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ANOVA
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the ''t''-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means. History While the analysis of variance reached fruition in the 20th century, antecedents extend centuries into the past according to Stigler. These include hypothesis testing, the partitioning of sums of squares, experimental techniques and the additive model. Laplace was performing hypothesis testing i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Effects Model
In statistics, a fixed effects model is a statistical model in which the model parameters are fixed or non-random quantities. This is in contrast to random effects models and mixed models in which all or some of the model parameters are random variables. In many applications including econometrics and biostatistics a fixed effects model refers to a regression model in which the group means are fixed (non-random) as opposed to a random effects model in which the group means are a random sample from a population. Generally, data can be grouped according to several observed factors. The group means could be modeled as fixed or random effects for each grouping. In a fixed effects model each group mean is a group-specific fixed quantity. In panel data where longitudinal observations exist for the same subject, fixed effects represent the subject-specific means. In panel data analysis the term fixed effects estimator (also known as the within estimator) is used to refer to an estimator ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Effects Model
In statistics, a random effects model, also called a variance components model, is a statistical model where the model parameters are random variables. It is a kind of hierarchical linear model, which assumes that the data being analysed are drawn from a hierarchy of different populations whose differences relate to that hierarchy. A random effects model is a special case of a mixed model. Contrast this to the biostatistics definitions, as biostatisticians use "fixed" and "random" effects to respectively refer to the population-average and subject-specific effects (and where the latter are generally assumed to be unknown, latent variables). Qualitative description Random effect models assist in controlling for unobserved heterogeneity when the heterogeneity is constant over time and not correlated with independent variables. This constant can be removed from longitudinal data through differencing, since taking a first difference will remove any time invariant components of the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixed Model
A mixed model, mixed-effects model or mixed error-component model is a statistical model containing both fixed effects and random effects. These models are useful in a wide variety of disciplines in the physical, biological and social sciences. They are particularly useful in settings where repeated measurements are made on the same statistical units (longitudinal study), or where measurements are made on clusters of related statistical units. Because of their advantage in dealing with missing values, mixed effects models are often preferred over more traditional approaches such as repeated measures analysis of variance. This page will discuss mainly linear mixed-effects models (LMEM) rather than generalized linear mixed models or nonlinear mixed-effects models. History and current status Ronald Fisher introduced random effects models to study the correlations of trait values between relatives. In the 1950s, Charles Roy Henderson provided best linear unbiased estimates of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphericity
Sphericity is a measure of how closely the shape of an object resembles that of a perfect sphere. For example, the sphericity of the balls inside a ball bearing determines the quality of the bearing, such as the load it can bear or the speed at which it can turn without failing. Sphericity is a specific example of a compactness measure of a shape. Defined by Wadell in 1935, the sphericity, \Psi , of a particle is the ratio of the surface area of a sphere with the same volume as the given particle to the surface area of the particle: :\Psi = \frac where V_p is volume of the particle and A_p is the surface area of the particle. The sphericity of a sphere is unity by definition and, by the isoperimetric inequality, any particle which is not a sphere will have sphericity less than 1. Sphericity applies in three dimensions; its analogue in two dimensions, such as the cross sectional circles along a cylindrical object such as a shaft, is called roundness. Ellipsoidal objects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greenhouse–Geisser Correction
The Greenhouse–Geisser correction \widehat is a statistical method of adjusting for lack of sphericity in a repeated measures ANOVA. The correction functions as both an estimate of epsilon (sphericity) and a correction for lack of sphericity. The correction was proposed by Samuel Greenhouse and Seymour Geisser in 1959. The Greenhouse–Geisser correction is an estimate of sphericity (\widehat). If sphericity is met, then \varepsilon = 1 . If sphericity is not met, then epsilon will be less than 1 (and the degrees of freedom will be overestimated and the F-value will be inflated). To correct for this inflation, multiply the Greenhouse–Geisser estimate of epsilon to the degrees of freedom used to calculate the F critical value. An alternative correction that is believed to be less conservative is the Huynh–Feldt correction (1976). As a general rule of thumb, the Greenhouse–Geisser correction is the preferred correction method when the epsilon estimate is below 0.75. Otherw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary. Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the estimate of a parameter is called the degrees of freedom. In general, the degrees of freedom of an estimate of a parameter are equal to the number of independent scores that go into the estimate minus the number of parameters used as intermediate steps in the estimation of the parameter itself. For example, if the variance is to be estimated from a random sample of ''N'' independent scores, then the degrees of freedom is equal to the number of independent scores (''N'') minus the number of parameters estimated as intermediate steps (one, namely, the sample mean) and is therefore equal to ''N'' − 1. Mathematically, degrees of freedom is the number of dimensions of the domain o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Restricted Randomization
In statistics, restricted randomization occurs in the design of experiments and in particular in the context of randomized experiments and randomized controlled trials. Restricted randomization allows intuitively poor allocations of treatments to experimental units to be avoided, while retaining the theoretical benefits of randomization. For example, in a clinical trial of a new proposed treatment of obesity compared to a control, an experimenter would want to avoid outcomes of the randomization in which the new treatment was allocated only to the heaviest patients. The concept was introduced by Frank Yates (1948) and William J. Youden (1972) "as a way of avoiding bad spatial patterns of treatments in designed experiments." Example of nested data Consider a batch process that uses 7 monitor wafers in each run. The plan further calls for measuring a response variable on each wafer at each of 9 sites. The organization of the sampling plan has a hierarchical or nested structure: the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
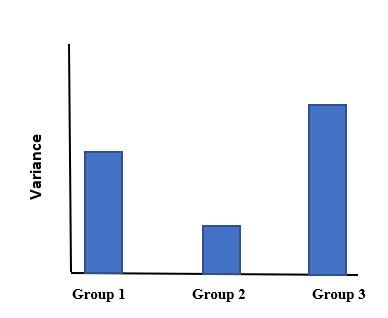
Mauchly's Sphericity Test
Mauchly's sphericity test or Mauchly's ''W'' is a statistical test used to validate a repeated measures analysis of variance (ANOVA). It was developed in 1940 by John Mauchly. Sphericity Sphericity is an important assumption of a repeated-measures ANOVA. It is the condition of equal variances among the differences between all possible pairs of within-subject conditions (i.e., levels of the independent variable). If sphericity is violated (i.e., if the variances of the differences between all combinations of the conditions are not equal), then the variance calculations may be distorted, which would result in an inflated F-ratio. Sphericity can be evaluated when there are three or more levels of a repeated measure factor and, with each additional repeated measures factor, the risk for violating sphericity increases. If sphericity is violated, a decision must be made as to whether a univariate or multivariate analysis is selected. If a univariate method is selected, the repeated-mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |