|
Mie Potential
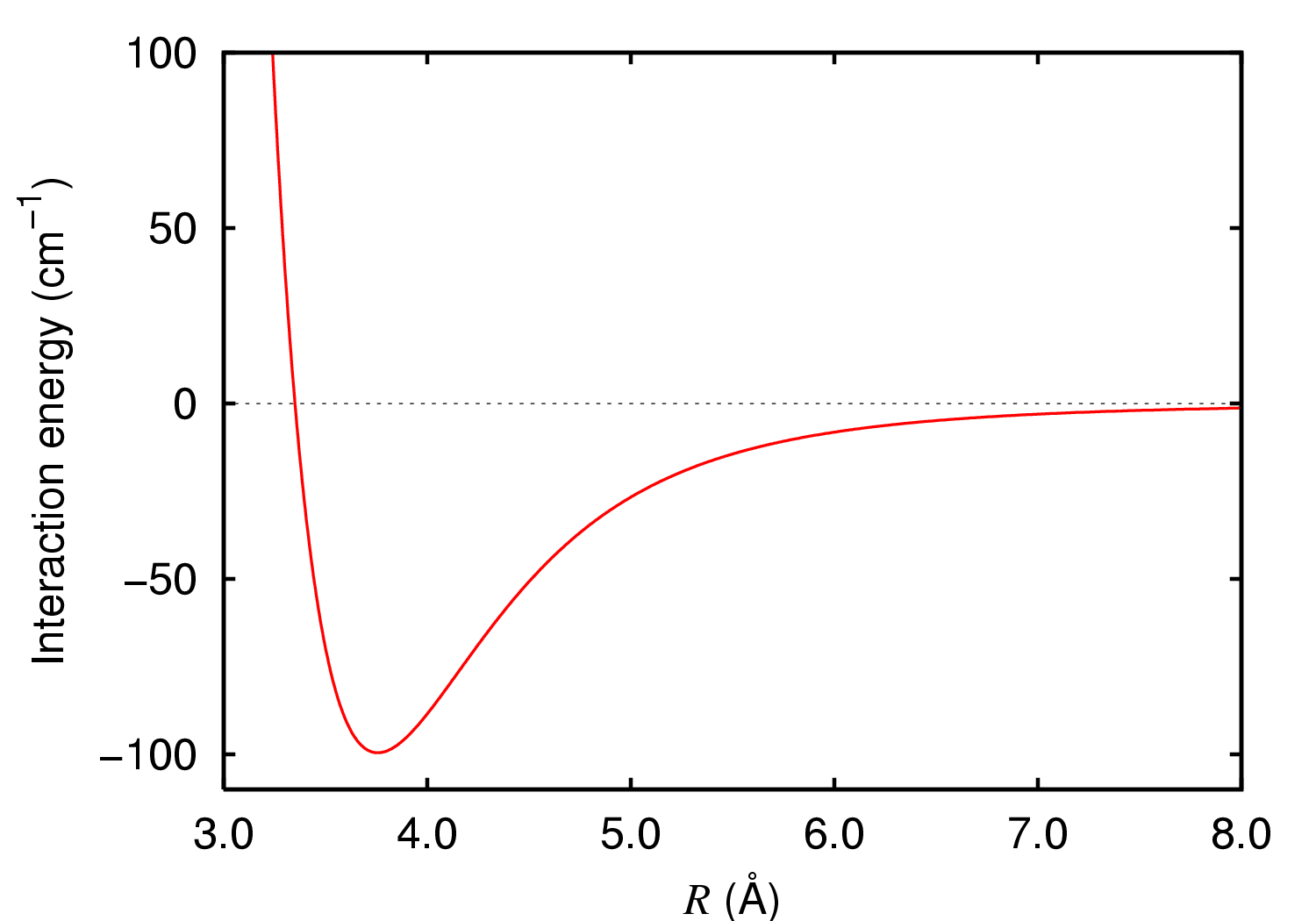
The Mie potential is an intermolecular pair potential, i.e. it describes the interactions between particles at the atomic level. The model is attributed to the German physicist Gustave Mie. The Mie potential is the generalized case of the Lennard-Jones (LJ) potential, which is perhaps the single most widely used pair potential. The Mie potential V(r) is a function of r, the distance between two particles, and is written as V(r) = C \, \varepsilon \left \left(\frac \right)^- \left( \frac\right)^m \right,~~~~~~ (1) with C = \frac \left( \frac\right)^ . The Lennard-Jones potential corresponds to the special case where n=12 and m=6 in Eq. (1). In Eq. (1), \varepsilon is the dispersion energy, and \sigma indicates the distance at which V = 0 , which is sometimes called the "collision radius." The parameter \sigma is generally indicative of the size of the particles involved in the collision. The parameters n and m characterize the shape of the potential: n describes the char ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pair Potential
In physics, a pair potential is a function that describes the potential energy of two interacting objects solely as a function of the distance between them. Examples of pair potentials include the Coulomb's law in electrodynamics, Newton's law of universal gravitation in mechanics, and the Lennard-Jones potential and the Morse potential in computational chemistry. Pair potentials are very common in physics and computational chemistry and biology; exceptions are very rare. An example of a potential energy function that is ''not'' a pair potential is the three-body Axilrod-Teller potential. Another example is the Stillinger-Weber potential for silicon Silicon is a chemical element with the symbol Si and atomic number 14. It is a hard, brittle crystalline solid with a blue-grey metallic luster, and is a tetravalent metalloid and semiconductor. It is a member of group 14 in the periodic ta ..., which includes the angle in a triangle of silicon atoms as an input paramete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gustav Mie
Gustav Adolf Feodor Wilhelm Ludwig Mie (; 29 September 1868 – 13 February 1957) was a German physicist. Life Mie was born in Rostock, Mecklenburg-Schwerin, Germany in 1868. From 1886 he studied mathematics and physics at the University of Rostock. In addition to his major subjects, he also attended lectures in chemistry, zoology, geology, mineralogy and astronomy, as well as logic and metaphysics. In 1889 he continued his studies at the University of Heidelberg and received a doctoral degree in mathematics at the age of 22. In 1897 he got his habilitation at the University of Göttingen in theoretical physics and in 1902 became extraordinary professor for theoretical physics at the University of Greifswald. In 1917 he became full professor for experimental physics at Martin Luther University of Halle-Wittenberg. In 1924 he became professor at the University of Freiburg, where he worked up to his retirement in 1935. In Freiburg, during the Nazi dictatorship, Mie was member ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lennard-Jones Potential
The Lennard-Jones potential (also termed the LJ potential or 12-6 potential) is an intermolecular pair potential. Out of all the intermolecular potentials, the Lennard-Jones potential is probably the one that has been the most extensively studied. It is considered an archetype model for simple yet realistic intermolecular interactions. The Lennard-Jones potential models soft repulsive and attractive ( van der Waals) interactions. Hence, the Lennard-Jones potential describes electronically neutral atoms or molecules. It is named after John Lennard-Jones. The commonly used expression for the Lennard-Jones potential is V_\text(r) = 4\varepsilon \left \left(\frac\right)^ - \left(\frac\right)^6 \right, where r is the distance between two interacting particles, \varepsilon is the depth of the potential well (usually referred to as 'dispersion energy'), and \sigma is the distance at which the particle-particle potential energy V is zero (often referred to as 'size of the particle'). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
London Dispersion Force
London dispersion forces (LDF, also known as dispersion forces, London forces, instantaneous dipole–induced dipole forces, fluctuating induced dipole bonds or loosely as van der Waals forces) are a type of intermolecular force acting between atoms and molecules that are normally electrically symmetric; that is, the electrons are symmetrically distributed with respect to the nucleus. They are part of the van der Waals forces. The LDF is named after the German physicist Fritz London. They are the weakest intermolecular force. Introduction The electron distribution around an atom or molecule undergoes fluctuations in time. These fluctuations create instantaneous electric fields which are felt by other nearby atoms and molecules, which in turn adjust the spatial distribution of their own electrons. The net effect is that the fluctuations in electron positions in one atom induce a corresponding redistribution of electrons in other atoms, such that the electron motions become corre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressibility
In thermodynamics and fluid mechanics, the compressibility (also known as the coefficient of compressibility or, if the temperature is held constant, the isothermal compressibility) is a measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure (or mean stress) change. In its simple form, the compressibility \kappa (denoted in some fields) may be expressed as :\beta =-\frac\frac, where is volume and is pressure. The choice to define compressibility as the negative of the fraction makes compressibility positive in the (usual) case that an increase in pressure induces a reduction in volume. The reciprocal of compressibility at fixed temperature is called the isothermal bulk modulus. Definition The specification above is incomplete, because for any object or system the magnitude of the compressibility depends strongly on whether the process is isentropic or isothermal. Accordingly, isothermal compressibility is defined: :\beta_T=-\frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speed Of Sound
The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. At , the speed of sound in air is about , or one kilometre in or one mile in . It depends strongly on temperature as well as the medium through which a sound wave is propagating. At , the speed of sound in air is about . The speed of sound in an ideal gas depends only on its temperature and composition. The speed has a weak dependence on frequency and pressure in ordinary air, deviating slightly from ideal behavior. In colloquial speech, ''speed of sound'' refers to the speed of sound waves in air. However, the speed of sound varies from substance to substance: typically, sound travels most slowly in gases, faster in liquids, and fastest in solids. For example, while sound travels at in air, it travels at in water (almost 4.3 times as fast) and at in iron (almost 15 times as fast). In an exceptionally stiff material such as diamond, sound travels a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Force Field (chemistry)
In the context of chemistry and molecular modelling, a force field is a computational method that is used to estimate the forces between atoms within molecules and also between molecules. More precisely, the force field refers to the functional form and parameter sets used to calculate the potential energy of a system of atoms or coarse-grained particles in molecular mechanics, molecular dynamics, or Monte Carlo simulations. The parameters for a chosen energy function may be derived from experiments in physics and chemistry, calculations in quantum mechanics, or both. Force fields are interatomic potentials and utilize the same concept as force fields in classical physics, with the difference that the force field parameters in chemistry describe the energy landscape, from which the acting forces on every particle are derived as a gradient of the potential energy with respect to the particle coordinates. ''All-atom'' force fields provide parameters for every type of atom in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Modelling
Molecular modelling encompasses all methods, theoretical and computational, used to model or mimic the behaviour of molecules. The methods are used in the fields of computational chemistry, drug design, computational biology and materials science to study molecular systems ranging from small chemical systems to large biological molecules and material assemblies. The simplest calculations can be performed by hand, but inevitably computers are required to perform molecular modelling of any reasonably sized system. The common feature of molecular modelling methods is the atomistic level description of the molecular systems. This may include treating atoms as the smallest individual unit (a molecular mechanics approach), or explicitly modelling protons and neutrons with its quarks, anti-quarks and gluons and electrons with its photons (a quantum chemistry approach). Molecular mechanics Molecular mechanics is one aspect of molecular modelling, as it involves the use of classical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virial Coefficient
Virial coefficients B_i appear as coefficients in the virial expansion of the pressure of a many-particle system in powers of the density, providing systematic corrections to the ideal gas law. They are characteristic of the interaction potential between the particles and in general depend on the temperature. The second virial coefficient B_2 depends only on the pair interaction between the particles, the third (B_3) depends on 2- and non-additive 3-body interactions, and so on. Derivation The first step in obtaining a closed expression for virial coefficients is a cluster expansion of the grand canonical partition function : \Xi = \sum_ = e^ Here p is the pressure, V is the volume of the vessel containing the particles, k_B is Boltzmann's constant, T is the absolute temperature, \lambda =\exp mu/(k_BT) is the fugacity, with \mu the chemical potential. The quantity Q_n is the canonical partition function of a subsystem of n particles: : Q_n = \operatorname e^ Here H(1,2,\ld ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects (e.g. water striders) to float on a water surface without becoming even partly submerged. At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion). There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract. Second is a tangential force parallel to the surface of the liquid. This ''tangential'' force is generally referred to as the surface tension. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane. But this analogy must not be taken too far as the tension in an elastic membrane is dependent on the amount of deformation of the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vapor–liquid Equilibrium
In thermodynamics and chemical engineering, the vapor–liquid equilibrium (VLE) describes the distribution of a chemical species between the vapor phase and a liquid phase. The concentration of a vapor in contact with its liquid, especially at equilibrium, is often expressed in terms of vapor pressure, which will be a partial pressure (a part of the total gas pressure) if any other gas(es) are present with the vapor. The equilibrium vapor pressure of a liquid is in general strongly dependent on temperature. At vapor–liquid equilibrium, a liquid with individual components in certain concentrations will have an equilibrium vapor in which the concentrations or partial pressures of the vapor components have certain values depending on all of the liquid component concentrations and the temperature. The converse is also true: if a vapor with components at certain concentrations or partial pressures is in vapor–liquid equilibrium with its liquid, then the component concentration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics applies to a wide variety of topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering and mechanical engineering, but also in other complex fields such as meteorology. Historically, thermodynamics developed out of a desire to increase the efficiency of early steam engines, particularly through the work of French physicist Sadi Carnot (1824) who believed that engine efficiency was the key that could help France win the Napoleonic Wars. Scots-Irish physicist Lord Kelvin was the first to formulate a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

_-_filtered.jpg)


