|
Metric Interval Temporal Logic
In model checking, the Metric Interval Temporal Logic (MITL) is a fragment of Metric Temporal Logic (MTL). This fragment is often preferred to MTL because some problems that are undecidable for MTL become decidable for MITL. Definition A MITL formula is an MTL formula, such that each set of reals used in subscript are intervals, which are not singletons, and whose bounds are either a natural number or are infinite. Difference from MTL MTL can express a statement such as the sentence S: "P held exactly ten time units ago". This is impossible in MITL. Instead, MITL can say T: "P held between 9 and 10 time units ago". Since MITL can express T but not S, in a sense, MITL is a restriction of MTL which allows only less precise statements. Problems that MITL avoids One reason to want to avoid a statement such as S is that its truth value may change an arbitrary number of times in a single time unit. Indeed, the truth value of this statement may change as many times as the truth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Model Checking
In computer science, model checking or property checking is a method for checking whether a finite-state model of a system meets a given specification (also known as correctness). This is typically associated with hardware or software systems, where the specification contains liveness requirements (such as avoidance of livelock) as well as safety requirements (such as avoidance of states representing a system crash). In order to solve such a problem algorithmically, both the model of the system and its specification are formulated in some precise mathematical language. To this end, the problem is formulated as a task in logic, namely to check whether a structure satisfies a given logical formula. This general concept applies to many kinds of logic and many kinds of structures. A simple model-checking problem consists of verifying whether a formula in the propositional logic is satisfied by a given structure. Overview Property checking is used for verification when two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Undecidable Problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is proved to be impossible to construct an algorithm that always leads to a correct yes-or-no answer. The halting problem is an example: it can be proven that there is no algorithm that correctly determines whether an arbitrary program eventually halts when run. Background A decision problem is a question which, for every input in some infinite set of inputs, requires a "yes" or "no" answer. Those inputs can be numbers (for example, the decision problem "is the input a prime number?") or values of some other kind, such as strings of a formal language. The formal representation of a decision problem is a subset of the natural numbers. For decision problems on natural numbers, the set consists of those numbers that the decision problem answers "yes" to. For example, the decision problem "is the input even?" is formalized as the set of even numbers. A decision pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Decidable Problem
In computability theory and computational complexity theory, a decision problem is a computational problem that can be posed as a yes–no question on a set of input values. An example of a decision problem is deciding whether a given natural number is prime. Another example is the problem, "given two numbers ''x'' and ''y'', does ''x'' evenly divide ''y''?" A decision procedure for a decision problem is an algorithmic method that answers the yes-no question on all inputs, and a decision problem is called decidable if there is a decision procedure for it. For example, the decision problem "given two numbers ''x'' and ''y'', does ''x'' evenly divide ''y''?" is decidable since there is a decision procedure called long division that gives the steps for determining whether ''x'' evenly divides ''y'' and the correct answer, ''YES'' or ''NO'', accordingly. Some of the most important problems in mathematics are undecidable, e.g. the halting problem. The field of computational compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Timed Automaton
timed (time daemon) is an operating system program that maintains the system time in synchronization with time servers using the Time Synchronization Protocol (TSP) developed by Riccardo Gusella and Stefano Zatti. Gusella and Zatti had done earlier related work on their TEMPO algorithm. The Time Synchronization Protocol specification refers to an election algorithm and a synchronization mechanism specified in other technical reports listed as "to appear". With the release of macOS High Sierra in 2017, timed in macOS has subsumed all time synchronization responsibilities including those of the former ntpd and timed. See also * Network Time Protocol (NTP) * Precision Time Protocol (IEEE 1588 PTP) References External links timed(8) man page* ', System Manager's Manual (SMM:11) * ', System Manager's Manual (SMM:12) Network time-related software {{operating-system-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
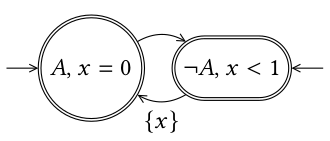
Signal Automaton
In automata theory, a field of computer science, a signal automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a signal automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset. Example Before formally defining what a signal automaton is, an example will be given. Let one consider the language \mathcal L of signals, over a binary alphabet \, which contains signals \gamma such that: * A appears in singular intervals. That is, the set of times \ is discrete, and * A appears at least once during each interval of length one. This language can be accepted by the automaton pictured nearby. As for finite automaton, incoming arrows represents initial locations and double circle represents accepting l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Signal (model Checking)
In model checking, a subfield of computer science, a signal or timed state sequence is an extension of the notion of words in a formal language, in which letters are continuously emitted. While a word is traditionally defined as a function from a set of non-negative integers to letters, a signal is a function from a set of real numbers to letters. This allow the use of formalisms similar to the ones of automata theory to deal with continuous signals. Example Consider an elevator. What is formally called a letter could be in fact information such as "someone is pressing the button on the 2nd floor", or "the doors are currently open on the third floor". In this case, a signal indicates, at each time, which is the current state of the elevator and its buttons. The signal can then be analyzed using formal methods to check whether a property such that "each time the elevator is called, it arrives in less than three minutes, assuming that no one held the door for more than fifteen seco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
PSPACE-complete
In computational complexity theory, a decision problem is PSPACE-complete if it can be solved using an amount of memory that is polynomial in the input length (PSPACE, polynomial space) and if every other problem that can be solved in polynomial space can be Polynomial-time reduction, transformed to it in polynomial time. The problems that are PSPACE-complete can be thought of as the hardest problems in PSPACE, the class of decision problems solvable in polynomial space, because a solution to any one such problem could easily be used to solve any other problem in PSPACE. Problems known to be PSPACE-complete include determining properties of regular expressions and context-sensitive grammars, determining the truth of quantified Boolean formula problem, quantified Boolean formulas, step-by-step changes between solutions of combinatorial optimization problems, and many puzzles and games. Theory A problem is defined to be PSPACE-complete if it can be solved using a polynomial amount o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Temporal Logic
In logic, temporal logic is any system of rules and symbolism for representing, and reasoning about, propositions qualified in terms of time (for example, "I am ''always'' hungry", "I will ''eventually'' be hungry", or "I will be hungry ''until'' I eat something"). It is sometimes also used to refer to tense logic, a modal logic-based system of temporal logic introduced by Arthur Prior in the late 1950s, with important contributions by Hans Kamp. It has been further developed by computer scientists, notably Amir Pnueli, and logicians. Temporal logic has found an important application in formal verification, where it is used to state requirements of hardware or software systems. For instance, one may wish to say that ''whenever'' a request is made, access to a resource is ''eventually'' granted, but it is ''never'' granted to two requestors simultaneously. Such a statement can conveniently be expressed in a temporal logic. Motivation Consider the statement "I am hungry". Though it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |