|
Maxima CAS
Maxima () is a computer algebra system (CAS) based on a 1982 version of Macsyma. It is written in Common Lisp and runs on all POSIX platforms such as macOS, Unix, BSD, and Linux, as well as under Microsoft Windows and Android. It is free software released under the terms of the GNU General Public License (GPL). History Maxima is based on a 1982 version of Macsyma, which was developed at MIT with funding from the United States Department of Energy and other government agencies. A version of Macsyma was maintained by Bill Schelter from 1982 until his death in 2001. In 1998, Schelter obtained permission from the Department of Energy to release his version under the GPL. That version, now called Maxima, is maintained by an independent group of users and developers. Maxima does not include any of the many modifications and enhancements made to the commercial version of Macsyma during 1982–1999. Though the core functionality remains similar, code depending on these enhancements may no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Project MAC
Computer Science and Artificial Intelligence Laboratory (CSAIL) is a research institute at the Massachusetts Institute of Technology (MIT) formed by the 2003 merger of the Laboratory for Computer Science (LCS) and the Artificial Intelligence Laboratory (AI Lab). Housed within the Ray and Maria Stata Center, CSAIL is the largest on-campus laboratory as measured by research scope and membership. It is part of the Schwarzman College of Computing but is also overseen by the MIT Vice President of Research. Research activities CSAIL's research activities are organized around a number of semi-autonomous research groups, each of which is headed by one or more professors or research scientists. These groups are divided up into seven general areas of research: * Artificial intelligence * Computational biology * Graphics and vision * Language and learning * Theory of computation * Robotics * Systems (includes computer architecture, databases, distributed systems, networks and networked sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bill Schelter
William Frederick Schelter (1947 – July 30, 2001) was a professor of mathematics at The University of Texas at Austin and a Lisp developer and programmer. Schelter is credited with the development of the GNU Common Lisp (GCL) implementation of Common Lisp and the GPL'd version of the computer algebra system Macsyma called Maxima. Schelter authored Austin Kyoto Common Lisp (AKCL) under contract with IBM. AKCL formed the foundation for Axiom, another computer algebra system. AKCL eventually became GNU Common Lisp. He is also credited with the first port of the GNU C compiler to the Intel 386 architecture, used in the original implementation of the Linux kernel. Schelter obtained his at |
Symbolic Computation
In mathematics and computer science, computer algebra, also called symbolic computation or algebraic computation, is a scientific area that refers to the study and development of algorithms and software for manipulating mathematical expressions and other mathematical objects. Although computer algebra could be considered a subfield of scientific computing, they are generally considered as distinct fields because scientific computing is usually based on numerical computation with approximate floating point numbers, while symbolic computation emphasizes ''exact'' computation with expressions containing variables that have no given value and are manipulated as symbols. Software applications that perform symbolic calculations are called ''computer algebra systems'', with the term ''system'' alluding to the complexity of the main applications that include, at least, a method to represent mathematical data in a computer, a user programming language (usually different from the languag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' join ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Factorization
In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these factors are further restricted to prime numbers, the process is called prime factorization. When the numbers are sufficiently large, no efficient non-quantum integer factorization algorithm is known. However, it has not been proven that such an algorithm does not exist. The presumed difficulty of this problem is important for the algorithms used in cryptography such as RSA public-key encryption and the RSA digital signature. Many areas of mathematics and computer science have been brought to bear on the problem, including elliptic curves, algebraic number theory, and quantum computing. In 2019, Fabrice Boudot, Pierrick Gaudry, Aurore Guillevic, Nadia Heninger, Emmanuel Thomé and Paul Zimmermann factored a 240-digit (795-bit) number (RSA-240) utilizing approximately 900 core-years of computing power. The researchers estimated that a 1024-bit RSA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurent Series
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.. Definition The Laurent series for a complex function f(z) about a point c is given by f(z) = \sum_^\infty a_n(z-c)^n, where a_n and c are constants, with a_n defined by a line integral that generalizes Cauchy's integral formula: a_n =\frac\oint_\gamma \frac \, dz. The path of integration \gamma is counterclockwise around a Jordan curve enclosing c and lying in an annulus A in which f(z) is holomorphic (analytic). The expansion for f(z) will then be valid anywhere inside the annulus. The annulus is shown in red ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
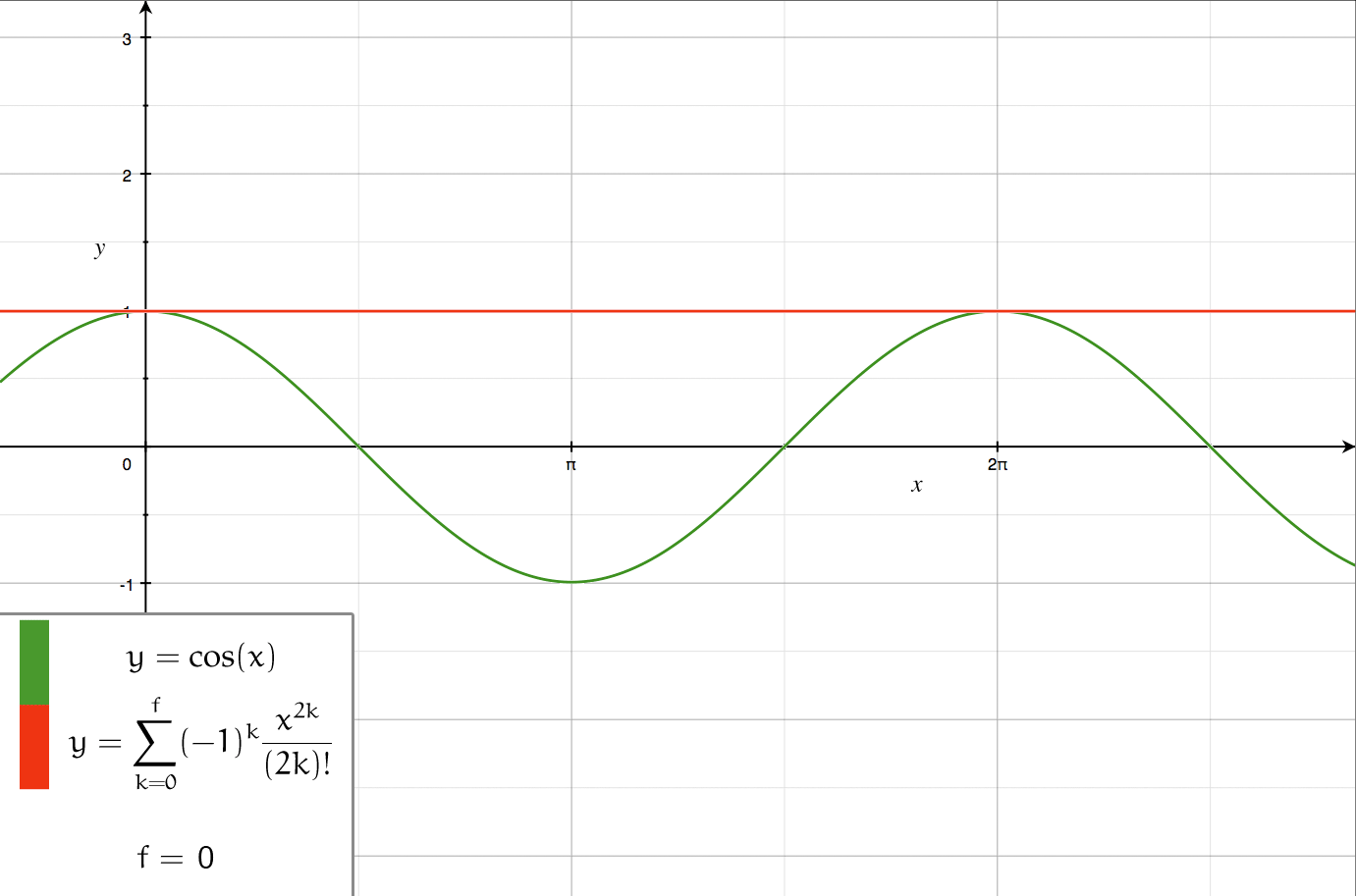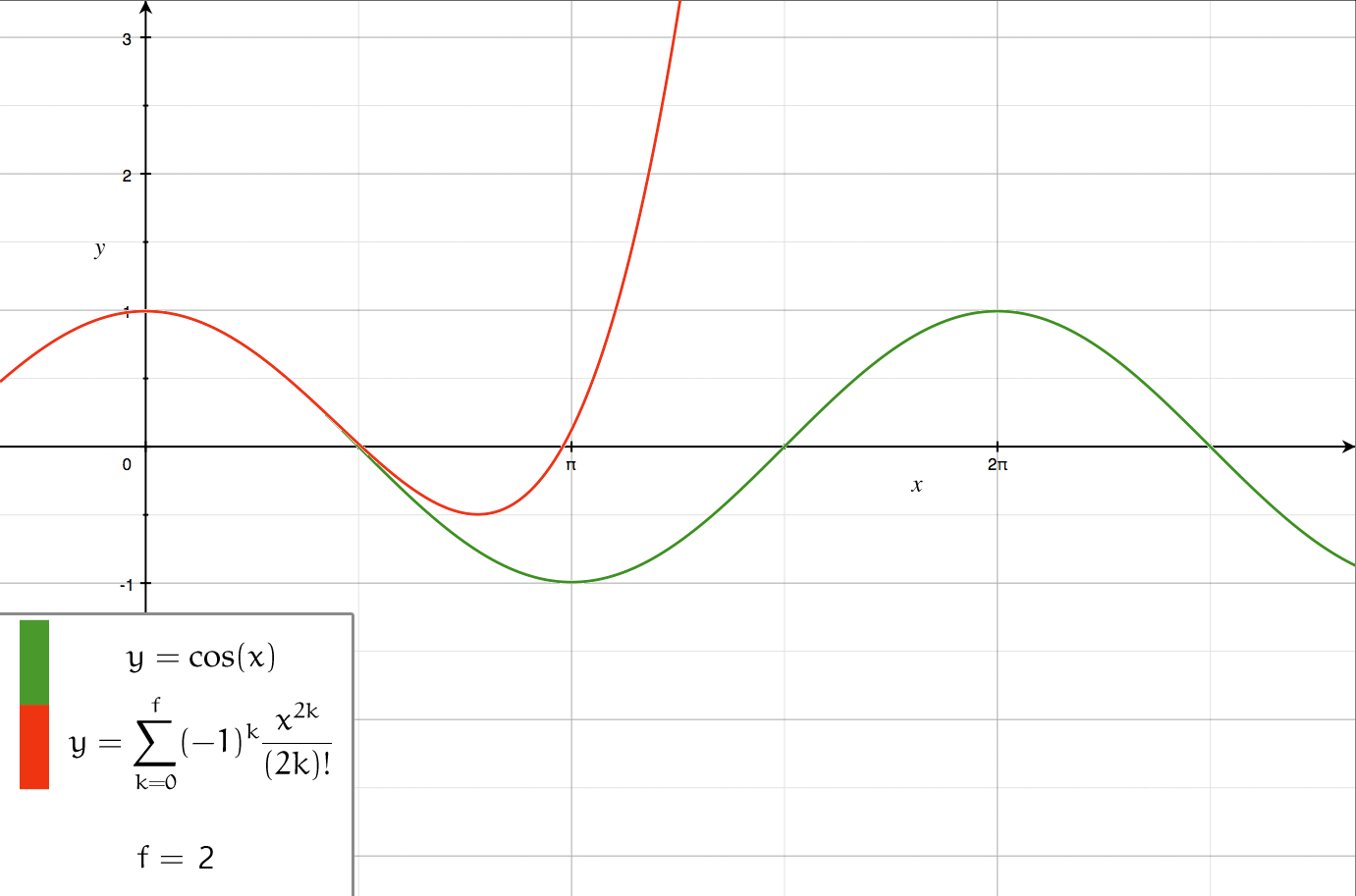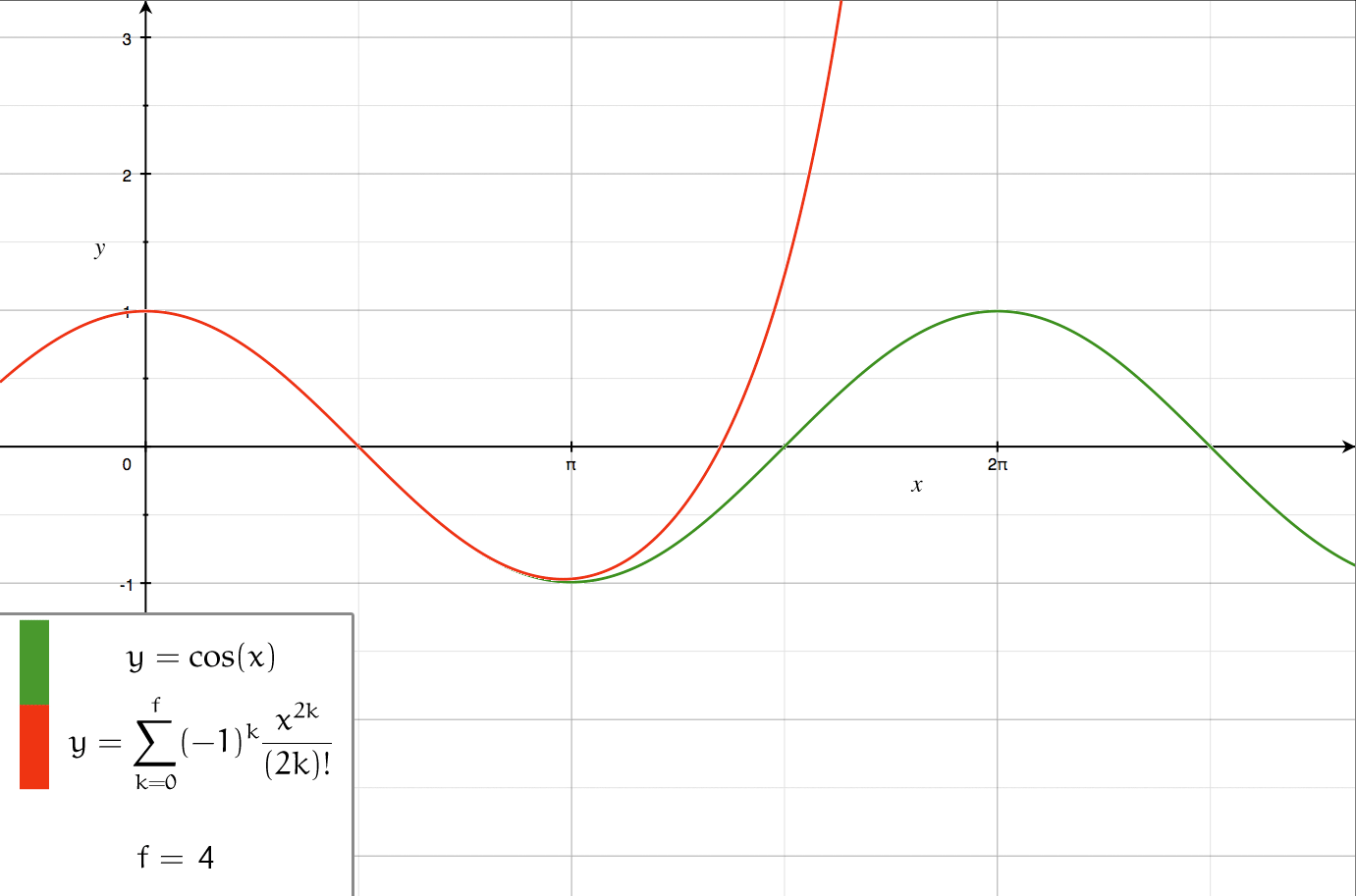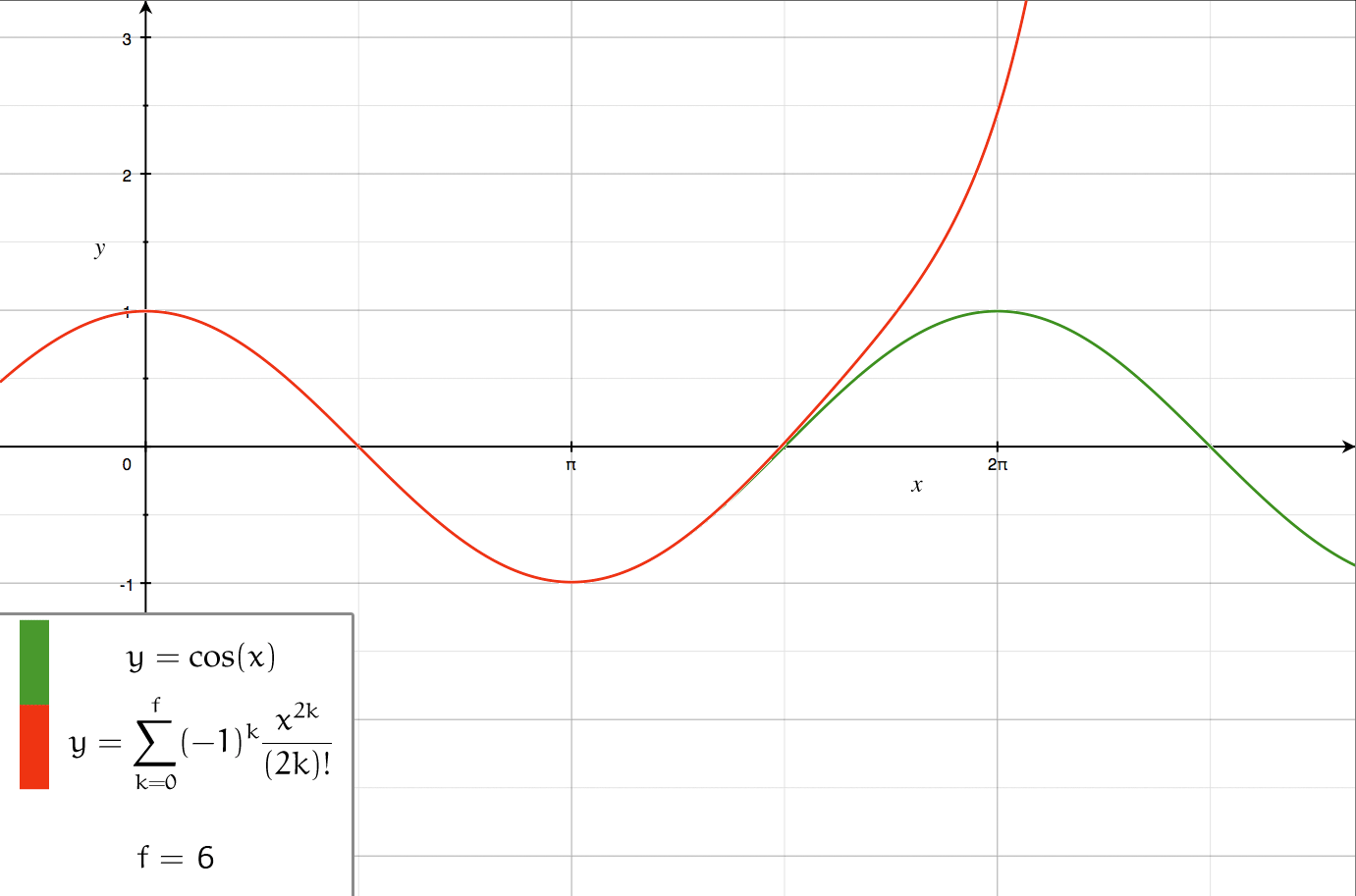
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series, when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series Expansion
In mathematics, a series expansion is an expansion of a function into a series, or infinite sum. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called ''series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. A ''Taylor series'' is a power series based on a function's derivatives at a single point. More specifically, if a function f: U\to\mathbb is infinitely differentiable around ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (mathematics)
In mathematics, a limit is the value that a function (or sequence) approaches as the input (or index) approaches some value. Limits are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals. The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory. In formulas, a limit of a function is usually written as : \lim_ f(x) = L, (although a few authors may use "Lt" instead of "lim") and is read as "the limit of of as approaches equals ". The fact that a function approaches the limit as approaches is sometimes denoted by a right arrow (→ or \rightarrow), as in :f(x) \to L \text x \to c, which reads "f of x tends to L as x tends to c". History Grégoire de Saint-Vincent gave the first definition of limit (terminus) of a geometric series in his work ''Opus Geometricum'' (1647): "The ''terminus'' of a pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Definite Integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be interpreted as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers satisfying is an interval which contains , , and all numbers in between. Other ... where the function is Riemann integrable is eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Greatest Common Divisor
In algebra, the greatest common divisor (frequently abbreviated as GCD) of two polynomials is a polynomial, of the highest possible degree, that is a factor of both the two original polynomials. This concept is analogous to the greatest common divisor of two integers. In the important case of univariate polynomials over a field the polynomial GCD may be computed, like for the integer GCD, by the Euclidean algorithm using long division. The polynomial GCD is defined only up to the multiplication by an invertible constant. The similarity between the integer GCD and the polynomial GCD allows extending to univariate polynomials all the properties that may be deduced from the Euclidean algorithm and Euclidean division. Moreover, the polynomial GCD has specific properties that make it a fundamental notion in various areas of algebra. Typically, the roots of the GCD of two polynomials are the common roots of the two polynomials, and this provides information on the roots without computi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
