|
MINQUE
In statistics, the theory of minimum norm quadratic unbiased estimation (MINQUE) was developed by C. R. Rao. Its application was originally to the problem of heteroscedasticity and the estimation of variance components in random effects model In statistics, a random effects model, also called a variance components model, is a statistical model where the model parameters are random variables. It is a kind of hierarchical linear model, which assumes that the data being analysed are dra ...s. The theory involves three stages: :*defining a general class of potential estimators as quadratic functions of the observed data, where the estimators relate to a vector of model parameters; :*specifying certain constraints on the desired properties of the estimators, such as unbiasedness; :*choosing the optimal estimator by minimising a "norm" which measures the size of the covariance matrix of the estimators. {{stats-stub, date=August 2016 References Estimation theory Statistical de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Effects Model
In statistics, a random effects model, also called a variance components model, is a statistical model where the model parameters are random variables. It is a kind of hierarchical linear model, which assumes that the data being analysed are drawn from a hierarchy of different populations whose differences relate to that hierarchy. A random effects model is a special case of a mixed model. Contrast this to the biostatistics definitions, as biostatisticians use "fixed" and "random" effects to respectively refer to the population-average and subject-specific effects (and where the latter are generally assumed to be unknown, latent variables). Qualitative description Random effect models assist in controlling for unobserved heterogeneity when the heterogeneity is constant over time and not correlated with independent variables. This constant can be removed from longitudinal data through differencing, since taking a first difference will remove any time invariant components of the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
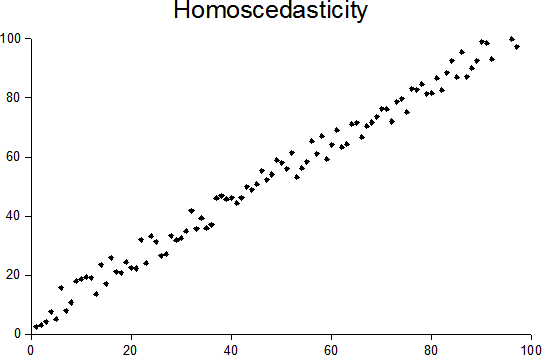
Heteroscedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Estimation Theory
Estimation theory is a branch of statistics that deals with estimating the values of parameters based on measured empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An '' estimator'' attempts to approximate the unknown parameters using the measurements. In estimation theory, two approaches are generally considered: * The probabilistic approach (described in this article) assumes that the measured data is random with probability distribution dependent on the parameters of interest * The set-membership approach assumes that the measured data vector belongs to a set which depends on the parameter vector. Examples For example, it is desired to estimate the proportion of a population of voters who will vote for a particular candidate. That proportion is the parameter sought; the estimate is based on a small random sample of voters. Alternatively, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |