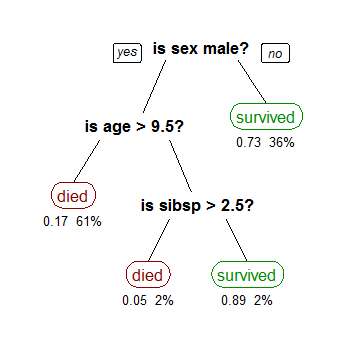|
Multivariate Statistics
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable. Multivariate statistics concerns understanding the different aims and background of each of the different forms of multivariate analysis, and how they relate to each other. The practical application of multivariate statistics to a particular problem may involve several types of univariate and multivariate analyses in order to understand the relationships between variables and their relevance to the problem being studied. In addition, multivariate statistics is concerned with multivariate probability distributions, in terms of both :*how these can be used to represent the distributions of observed data; :*how they can be used as part of statistical inference, particularly where several different quantities are of interest to the same analysis. Certain types of problems involving multivariate data, for example simple linear regression an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
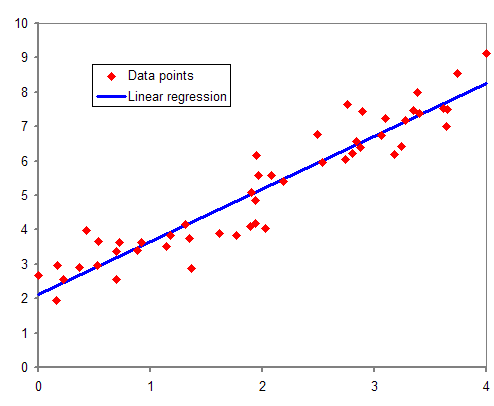
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Autoregression
Vector autoregression (VAR) is a statistical model used to capture the relationship between multiple quantities as they change over time. VAR is a type of stochastic process model. VAR models generalize the single-variable (univariate) autoregressive model by allowing for multivariate time series. VAR models are often used in economics and the natural sciences. Like the autoregressive model, each variable has an equation modelling its evolution over time. This equation includes the variable's lagged (past) values, the lagged values of the other variables in the model, and an error term. VAR models do not require as much knowledge about the forces influencing a variable as do structural models with simultaneous equations. The only prior knowledge required is a list of variables which can be hypothesized to affect each other over time. Specification Definition A VAR model describes the evolution of a set of ''k'' variables, called ''endogenous variables'', over time. Each perio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simultaneous Equations Model
Simultaneous equations models are a type of statistical model in which the dependent variables are functions of other dependent variables, rather than just independent variables. This means some of the explanatory variables are jointly determined with the dependent variable, which in economics usually is the consequence of some underlying equilibrium mechanism. Take the typical supply and demand model: whilst typically one would determine the quantity supplied and demanded to be a function of the price set by the market, it is also possible for the reverse to be true, where producers observe the quantity that consumers demand ''and then'' set the price. Simultaneity poses challenges for the estimation of the statistical parameters of interest, because the Gauss–Markov assumption of strict exogeneity of the regressors is violated. And while it would be natural to estimate all simultaneous equations at once, this often leads to a computationally costly non-linear optimization p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Coordinates
Parallel coordinates are a common way of visualizing and analyzing high-dimensional datasets. To show a set of points in an ''n''-dimensional space, a backdrop is drawn consisting of ''n'' parallel lines, typically vertical and equally spaced. A point in ''n''-dimensional space is represented as a polyline with vertices on the parallel axes; the position of the vertex on the ''i''-th axis corresponds to the ''i''-th coordinate of the point. This visualization is closely related to time series visualization, except that it is applied to data where the axes do not correspond to points in time, and therefore do not have a natural order. Therefore, different axis arrangements may be of interest. History Parallel coordinates were often said to be invented by Philbert Maurice d'Ocagne in 1885, but even though the words "Coordonnées parallèles" appear in the book title this work has nothing to do with the visualization techniques of the same name; the book only describes a met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Graphics
Statistical graphics, also known as statistical graphical techniques, are graphics used in the field of statistics for data visualization. Overview Whereas statistics and data analysis procedures generally yield their output in numeric or tabular form, graphical techniques allow such results to be displayed in some sort of pictorial form. They include plots such as scatter plots, histograms, probability plots, spaghetti plots, residual plots, box plots, block plots and biplots. Exploratory data analysis (EDA) relies heavily on such techniques. They can also provide insight into a data set to help with testing assumptions, model selection and regression model validation, estimator selection, relationship identification, factor effect determination, and outlier detection. In addition, the choice of appropriate statistical graphics can provide a convincing means of communicating the underlying message that is present in the data to others. Graphical statistical methods have fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artificial Neural Networks
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains. An ANN is based on a collection of connected units or nodes called artificial neurons, which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron receives signals then processes them and can signal neurons connected to it. The "signal" at a connection is a real number, and the output of each neuron is computed by some non-linear function of the sum of its inputs. The connections are called ''edges''. Neurons and edges typically have a ''weight'' that adjusts as learning proceeds. The weight increases or decreases the strength of the signal at a connection. Neurons may have a threshold such that a signal is sent only if the aggregate signal crosses that threshold. Typically, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursive Partitioning
Recursive partitioning is a statistical method for multivariable analysis. Recursive partitioning creates a decision tree that strives to correctly classify members of the population by splitting it into sub-populations based on several dichotomous independent variables. The process is termed recursive because each sub-population may in turn be split an indefinite number of times until the splitting process terminates after a particular stopping criterion is reached. Recursive partitioning methods have been developed since the 1980s. Well known methods of recursive partitioning include Ross Quinlan's ID3 algorithm and its successors, C4.5 and C5.0 and Classification and Regression Trees (CART). Ensemble learning methods such as Random Forests help to overcome a common criticism of these methods – their vulnerability to overfitting of the data – by employing different algorithms and combining their output in some way. This article focuses on recursive partitioning for medic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
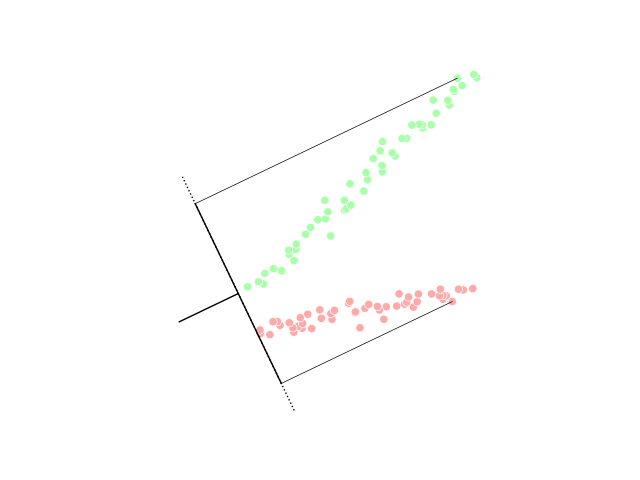
Cluster Analysis
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). It is a main task of exploratory data analysis, and a common technique for statistics, statistical data analysis, used in many fields, including pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Cluster analysis itself is not one specific algorithm, but the general task to be solved. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with small Distance function, distances between cluster members, dense areas of the data space, intervals or particular statistical distributions. Clustering can therefore be formulated as a multi-object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Discriminant Analysis
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical independent variables and a continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regression and probit regression are more similar to LDA than ANOVA is, as they also explain a categorical var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant Function
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical independent variables and a continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regression and probit regression are more similar to LDA than ANOVA is, as they also explain a categorical var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Coordinates Analysis
Multidimensional scaling (MDS) is a means of visualizing the level of similarity of individual cases of a dataset. MDS is used to translate "information about the pairwise 'distances' among a set of n objects or individuals" into a configuration of n points mapped into an abstract Cartesian space. More technically, MDS refers to a set of related ordination techniques used in information visualization, in particular to display the information contained in a distance matrix. It is a form of non-linear dimensionality reduction. Given a distance matrix with the distances between each pair of objects in a set, and a chosen number of dimensions, ''N'', an MDS algorithm places each object into ''N''-dimensional space (a lower-dimensional representation) such that the between-object distances are preserved as well as possible. For ''N'' = 1, 2, and 3, the resulting points can be visualized on a scatter plot. Core theoretical contributions to MDS were made by James O. Ramsay of Mc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |