|
Multivariate Analysis Of Covariance
Multivariate analysis of covariance (MANCOVA) is an extension of analysis of covariance (ANCOVA) methods to cover cases where there is more than one dependent variable and where the control of concomitant continuous independent variables – covariates – is required. The most prominent benefit of the MANCOVA design over the simple MANOVA is the 'factoring out' of statistical noise, noise or error that has been introduced by the covariant. A commonly used multivariate version of the ANOVA F-distribution, F-statistic is Wilks' lambda distribution, Wilks' Lambda (Λ), which represents the ratio between the error variance (or covariance) and the effect variance (or covariance). Statsoft Textbook, ANOVA/MANOVA. Goals Similarly to all tests in the ANOVA family, the primary aim of the MANCOVA is to test for significant ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Covariance
Analysis of covariance (ANCOVA) is a general linear model which blends ANOVA and regression. ANCOVA evaluates whether the means of a dependent variable (DV) are equal across levels of a categorical independent variable (IV) often called a treatment, while statistically controlling for the effects of other continuous variables that are not of primary interest, known as covariates (CV) or nuisance variables. Mathematically, ANCOVA decomposes the variance in the DV into variance explained by the CV(s), variance explained by the categorical IV, and residual variance. Intuitively, ANCOVA can be thought of as 'adjusting' the DV by the group means of the CV(s). The ANCOVA model assumes a linear relationship between the response (DV) and covariate (CV): y_ = \mu + \tau_i + \Beta(x_ - \overline) + \epsilon_. In this equation, the DV, y_ is the jth observation under the ith categorical group; the CV, x_ is the ''j''th observation of the covariate under the ''i''th group. Variables in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Levene's Test
In statistics, Levene's test is an inferential statistic used to assess the equality of variances for a variable calculated for two or more groups. Some common statistical procedures assume that variances of the populations from which different samples are drawn are equal. Levene's test assesses this assumption. It tests the null hypothesis that the population variances are equal (called ''homogeneity of variance'' or ''homoscedasticity''). If the resulting ''p''-value of Levene's test is less than some significance level (typically 0.05), the obtained differences in sample variances are unlikely to have occurred based on random sampling from a population with equal variances. Thus, the null hypothesis of equal variances is rejected and it is concluded that there is a difference between the variances in the population. Some of the procedures typically assuming homoscedasticity, for which one can use Levene's tests, include analysis of variance and t-tests. Levene's test is so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent Variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roy's Greatest Root
Roy's is an upscale American restaurant that specializes in Hawaiian and Japanese fusion cuisine, with a focus on sushi, seafood and steak. The chain was founded by James Beard Foundation Award Winner, Roy Yamaguchi in 1988 in Honolulu, Hawaii. The concept was well received among critics upon inception. The concept has grown to include 21 Roy's restaurants in the continental United States, six in Hawaii, one in Japan and one in Guam. Roy's is known best for its eclectic blend of Hawaiian, Japanese, and Classic French cuisine created by founder Roy Yamaguchi who was born in Tokyo, Japan, and spent his childhood visiting his grandparents who owned a tavern in Wailuku, Maui. Yamaguchi then graduated from the Culinary Institute of America where he received his formal culinary training and credits these factors to inspiring his unique culinary vision that is brought to life at Roy's. 20 mainland locations Roy's were owned and operated by Bloomin' Brands, Inc., until December 2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harold Hotelling
Harold Hotelling (; September 29, 1895 – December 26, 1973) was an American mathematical statistician and an influential economic theorist, known for Hotelling's law, Hotelling's lemma, and Hotelling's rule in economics, as well as Hotelling's T-squared distribution in statistics. He also developed and named the principal component analysis method widely used in finance, statistics and computer science. He was Associate Professor of Mathematics at Stanford University from 1927 until 1931, a member of the faculty of Columbia University from 1931 until 1946, and a Professor of Mathematical Statistics at the University of North Carolina at Chapel Hill from 1946 until his death. A street in Chapel Hill bears his name. In 1972, he received the North Carolina Award for contributions to science. Statistics Hotelling is known to statisticians because of Hotelling's T-squared distribution which is a generalization of the Student's t-distribution in multivariate setting, and its us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace Of A Matrix
In linear algebra, the trace of a square matrix , denoted , is defined to be the sum of elements on the main diagonal (from the upper left to the lower right) of . The trace is only defined for a square matrix (). It can be proved that the trace of a matrix is the sum of its (complex) eigenvalues (counted with multiplicities). It can also be proved that for any two matrices and . This implies that similar matrices have the same trace. As a consequence one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the th row and th column of . The entries of can be real numbers or (more generally) complex numbers. The trace is not d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Samuel Stanley Wilks
Samuel Stanley Wilks (June 17, 1906 – March 7, 1964) was an American mathematician and academic who played an important role in the development of mathematical statistics, especially in regard to practical applications. Early life and education Wilks was born in Little Elm, Texas and raised on a farm. He studied Industrial Arts at the North Texas State Teachers College in Denton, Texas, obtaining his bachelor's degree in 1926. He received his master's degree in mathematics in 1928 from the University of Texas. He obtained his Ph.D. at the University of Iowa under Everett F. Lindquist; his thesis dealt with a problem of statistical measurement in education, and was published in the '' Journal of Educational Psychology''. Career Wilks became an instructor in mathematics at Princeton University in 1933; in 1938 he assumed the editorship of the journal '' Annals of Mathematical Statistics'' in place of Harry C. Carver. Wilks assembled an advisory board for the journal t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Value Decomposition
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix. It generalizes the eigendecomposition of a square normal matrix with an orthonormal eigenbasis to any \ m \times n\ matrix. It is related to the polar decomposition. Specifically, the singular value decomposition of an \ m \times n\ complex matrix is a factorization of the form \ \mathbf = \mathbf\ , where is an \ m \times m\ complex unitary matrix, \ \mathbf\ is an \ m \times n\ rectangular diagonal matrix with non-negative real numbers on the diagonal, is an n \times n complex unitary matrix, and \ \mathbf\ is the conjugate transpose of . Such decomposition always exists for any complex matrix. If is real, then and can be guaranteed to be real orthogonal matrices; in such contexts, the SVD is often denoted \ \mathbf^\mathsf\ . The diagonal entries \ \sigma_i = \Sigma_\ of \ \mathbf\ are uniquely determined by and are known as the singular values ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnitude (mathematics)
In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects of the same kind. More formally, an object's magnitude is the displayed result of an ordering (or ranking)—of the class of objects to which it belongs. In physics, magnitude can be defined as quantity or distance. History The Greeks distinguished between several types of magnitude, including: *Positive fractions *Line segments (ordered by length) * Plane figures (ordered by area) * Solids (ordered by volume) * Angles (ordered by angular magnitude) They proved that the first two could not be the same, or even isomorphic systems of magnitude. They did not consider negative magnitudes to be meaningful, and ''magnitude'' is still primarily used in contexts in which zero is either the smallest size or less than all possible sizes. Numbers The magnitude of any number x is usually called its '' absolute value'' or ''modulus'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
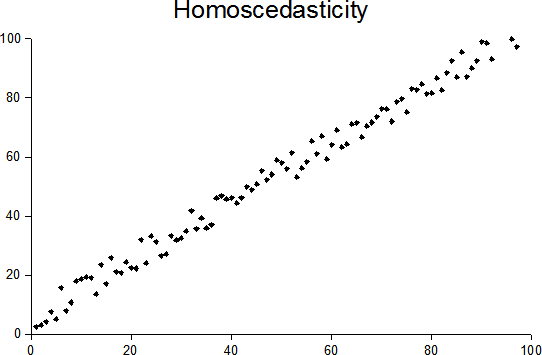
Heteroscedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |