|
Morphometrics
Morphometrics (from Greek μορΦή ''morphe'', "shape, form", and -μετρία ''metria'', "measurement") or morphometry refers to the quantitative analysis of ''form'', a concept that encompasses size and shape. Morphometric analyses are commonly performed on organisms, and are useful in analyzing their fossil record, the impact of mutations on shape, developmental changes in form, covariances between ecological factors and shape, as well for estimating quantitative-genetic parameters of shape. Morphometrics can be used to quantify a trait of evolutionary significance, and by detecting changes in the shape, deduce something of their ontogeny, function or evolutionary relationships. A major objective of morphometrics is to statistically test hypotheses about the factors that affect shape. "Morphometrics", in the broader sense, is also used to precisely locate certain areas of organs such as the brain, and in describing the shapes of other things. Forms Three general appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Procrustes Superimposition
In statistics, Procrustes analysis is a form of statistical shape analysis used to analyse the distribution of a set of shapes. The name '' Procrustes'' () refers to a bandit from Greek mythology who made his victims fit his bed either by stretching their limbs or cutting them off. In mathematics: * an orthogonal Procrustes problem is a method which can be used to find out the optimal ''rotation and/or reflection'' (i.e., the optimal orthogonal linear transformation) for the Procrustes Superimposition (PS) of an object with respect to another. * a constrained orthogonal Procrustes problem, subject to det(''R'') = 1 (where ''R'' is an orthogonal matrix), is a method which can be used to determine the optimal ''rotation'' for the PS of an object with respect to another (reflection is not allowed). In some contexts, this method is called the Kabsch algorithm. When a shape is compared to another, or a set of shapes is compared to an arbitrarily selected reference shape, Procruste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Thelodont Morphometrics
Thelodonti (from Greek: "nipple teeth")Maisey, John G., Craig Chesek, and David Miller. Discovering fossil fishes. New York: Holt, 1996. is a class of extinct Palaeozoic jawless fishes with distinctive scales instead of large plates of armor. There is much debate over whether the group represents a monophyletic grouping, or disparate stem groups to the major lines of jawless and jawed fish. Thelodonts are united in possession of " thelodont scales". This defining character is not necessarily a result of shared ancestry, as it may have been evolved independently by different groups. Thus the thelodonts are generally thought to represent a polyphyletic group, although there is no firm agreement on this point. On the basis that they are monophyletic, they are reconstructed as being ancestrally marine and invading freshwater on multiple occasions. "Thelodonts" were morphologically very similar, and probably closely related, to fish of the classes Heterostraci and Anaspida, dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Outline Analysis
Outline or outlining may refer to: * Outline (list), a document summary, in hierarchical list format * Code folding, a method of hiding or collapsing code or text to see content in outline form * Outline drawing, a sketch depicting the outer edges of a person or object, without interior details or shading * Outline typeface, in typography * Outline VPN, a free and open-source Shadowsocks deployment tool * Outline, the representation of a word in shorthand * Step outline, or just outline, the first summary of a story for a film script Media * ''Outline'' (novel), a 2014 novel by Rachel Cusk * ''Outlines'' (collection), a 1939 collection of poems by surrealist poet Jean Venturini * The Outline (website), a news company * Outlines Festival, an annual one-day music festival held in Sheffield, United Kingdom * Outline Records, record label founded by Jane Ira Bloom * The Outline (band), an experimental band from the United States * "Outlines" (song), by Mike Mago and Dragonette * "O ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
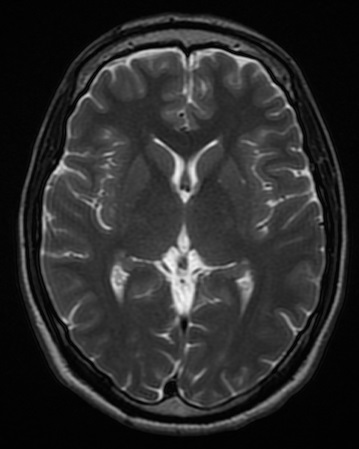
Voxel-based Morphometry
Voxel-based morphometry is a computational approach to neuroanatomy that measures differences in local concentrations of brain tissue, through a voxel-wise comparison of multiple brain images. In traditional morphometry, volume of the whole brain or List of regions in the human brain, its subparts is measured by drawing regions of interest (ROIs) on images from brain scanning and calculating the volume enclosed. However, this is time consuming and can only provide measures of rather large areas. Smaller differences in volume may be overlooked. The value of VBM is that it allows for comprehensive measurement of differences, not just in specific structures, but throughout the entire brain. VBM Image registration, registers every brain to a template, which gets rid of most of the large differences in brain anatomy among people. Then the brain images are smoothed so that each voxel represents the average of itself and its neighbors. Finally, the image volume is compared across brains a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Magnetic Resonance Imaging Of The Brain
Magnetic resonance imaging of the brain uses magnetic resonance imaging (MRI) to produce high-quality two- or three-dimensional images of the brain, brainstem, and cerebellum without ionizing radiation (X-rays) or radioactive tracers. History The first MR images of a human brain were obtained in 1978 by two groups of researchers at EMI Laboratories led by Ian Robert Young and Hugh Clow. In 1986, Charles L. Dumoulin and Howard R. Hart at General Electric developed MR angiography, and Denis Le Bihan obtained the first images and later patented diffusion MRI. In 1988, Arno Villringer and colleagues demonstrated that susceptibility contrast agents may be employed in perfusion MRI. In 1990, Seiji Ogawa at AT&T Bell labs recognized that oxygen-depleted blood with dHb was attracted to a magnetic field, and discovered the technique that underlies Functional Magnetic Resonance Imaging (fMRI). In the early 1980s to the early 1990s, 'Jedi' helmets, inspired by the 'Return of the Je ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Neuroimaging
Neuroimaging is the use of quantitative (computational) techniques to study the neuroanatomy, structure and function of the central nervous system, developed as an objective way of scientifically studying the healthy human brain in a non-invasive manner. Increasingly it is also being used for quantitative research studies of brain disease and psychiatric illness. Neuroimaging is highly multidisciplinary involving neuroscience, computer science, psychology and statistics, and is not a medical specialty. Neuroimaging is sometimes confused with neuroradiology. Neuroradiology is a medical specialty that uses non-statistical brain imaging in a clinical setting, practiced by radiologists who are medical practitioners. Neuroradiology primarily focuses on recognizing brain lesions, such as vascular diseases, strokes, tumors, and inflammatory diseases. In contrast to neuroimaging, neuroradiology is qualitative (based on subjective impressions and extensive clinical training) but sometime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
D'Arcy Wentworth Thompson
Sir D'Arcy Wentworth Thompson CB FRS FRSE (2 May 1860 – 21 June 1948) was a Scottish biologist, mathematician and classics scholar. He was a pioneer of mathematical and theoretical biology, travelled on expeditions to the Bering Strait and held the position of Professor of Natural History at University College, Dundee for 32 years, then at St Andrews for 31 years. He was elected a Fellow of the Royal Society, was knighted, and received the Darwin Medal and the Daniel Giraud Elliot Medal. Thompson is remembered as the author of the 1917 book '' On Growth and Form'', which led the way for the scientific explanation of morphogenesis, the process by which patterns and body structures are formed in plants and animals. Thompson's description of the mathematical beauty of nature, and the mathematical basis of the forms of animals and plants, stimulated thinkers as diverse as Julian Huxley, C. H. Waddington, Alan Turing, René Thom, Claude Lévi-Strauss, Eduardo Paolo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Thin Plate Splines
Thin plate splines (TPS) are a spline-based technique for data interpolation and smoothing. They were introduced to geometric design by Duchon. They are an important special case of a polyharmonic spline. Robust Point Matching (RPM) is a common extension and shortly known as the TPS-RPM algorithm. Physical analogy The name ''thin plate spline'' refers to a physical analogy involving the bending of a plate or thin sheet of metal. Just as the metal has rigidity, the TPS fit resists bending also, implying a penalty involving the smoothness of the fitted surface. In the physical setting, the deflection is in the z direction, orthogonal to the plane. In order to apply this idea to the problem of coordinate transformation, one interprets the lifting of the plate as a displacement of the x or y coordinates within the plane. In 2D cases, given a set of K corresponding control points (knots), the TPS warp is described by 2(K+3) parameters which include 6 global affine motion parameters and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Phylogenetic Relationship
In biology, phylogenetics () is the study of the evolutionary history of life using observable characteristics of organisms (or genes), which is known as Computational phylogenetics, phylogenetic inference. It infers the relationship among organisms based on empirical data and observed heritable traits of DNA sequences, protein amino acid sequences, and Morphology (biology), morphology. The results are a phylogenetic tree—a diagram depicting the hypothesis, hypothetical relationships among the organisms, reflecting their inferred evolutionary history. The tips of a phylogenetic tree represent the observed entities, which can be living Taxon, taxa or fossils. A phylogenetic diagram can be rooted or unrooted. A rooted tree diagram indicates the hypothetical common ancestor of the taxa represented on the tree. An unrooted tree diagram (a network) makes no assumption about directionality of character state transformation, and does not show the origin or "root" of the taxa in questi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Eigenvector
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi- dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Principal Component Analysis
Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing. The data is linearly transformed onto a new coordinate system such that the directions (principal components) capturing the largest variation in the data can be easily identified. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where the i-th vector is the direction of a line that best fits the data while being orthogonal to the first i-1 vectors. Here, a best-fitting line is defined as one that minimizes the average squared perpendicular distance from the points to the line. These directions (i.e., principal components) constitute an orthonormal basis in which different individual dimensions of the data are linearly uncorrelated. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Paleobiology (journal)
Paleobiology is a scientific journal promoting the integration of biology and conventional paleontology, with emphasis placed on biological or paleobiological processes and patterns. It attracts papers of interest to more than one discipline, and occasionally publishes research on recent organisms when this is of interest to paleontologists. Paleontology journals Academic journals published by learned and professional societies Academic journals established in 1975 Quarterly journals English-language journals Paleobiology Cambridge University Press academic journals {{paleontology-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |