|
Mode I Crack
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture. Theoretically, the stress ahead of a sharp crack tip becomes infinite and cannot be used to describe the state around a crack. Fracture mechanics is used to characterise the loads on a crack, typically using a single parameter to describe the complete loading state at the crack tip. A number of different parameters have been developed. When the plastic zone at the tip of the crack is small relative to the crack length the stress state at the crack tip is the result of elastic forces within the material and is termed linear elastic fracture mechanics (LEFM) and can be characterised using the stress intensity factor K. Although the load on a crack can be arbitrary, in 1957 G. Irwin found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fracture Modes V2
Fracture is the separation of an object or material into two or more pieces under the action of stress (physics), stress. The fracture of a solid usually occurs due to the development of certain displacement discontinuity surfaces within the solid. If a displacement develops perpendicular to the surface, it is called a normal tensile crack or simply a crack; if a displacement develops tangentially, it is called a shear crack, slip band or dislocation. Fracture#Brittle, Brittle fractures occur with no apparent deformation before fracture. Fracture#Ductile, Ductile fractures occur after visible deformation. Fracture strength, or breaking strength, is the stress when a specimen fails or fractures. The detailed understanding of how a fracture occurs and develops in materials is the object of fracture mechanics. Strength Fracture strength, also known as breaking strength, is the stress at which a specimen Structural integrity and failure, fails via fracture. This is usually de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brittle
A material is brittle if, when subjected to stress, it fractures with little elastic deformation and without significant plastic deformation. Brittle materials absorb relatively little energy prior to fracture, even those of high strength. Breaking is often accompanied by a sharp snapping sound. When used in materials science, it is generally applied to materials that fail when there is little or no plastic deformation before failure. One proof is to match the broken halves, which should fit exactly since no plastic deformation has occurred. Brittleness in different materials Polymers Mechanical characteristics of polymers can be sensitive to temperature changes near room temperatures. For example, poly(methyl methacrylate) is extremely brittle at temperature 4˚C, but experiences increased ductility with increased temperature. Amorphous polymers are polymers that can behave differently at different temperatures. They may behave like a glass at low temperatures (the glassy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Strain
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller (indeed, infinitesimally smaller) than any relevant dimension of the body; so that its geometry and the constitutive properties of the material (such as density and stiffness) at each point of space can be assumed to be unchanged by the deformation. With this assumption, the equations of continuum mechanics are considerably simplified. This approach may also be called small deformation theory, small displacement theory, or small displacement-gradient theory. It is contrasted with the finite strain theory where the opposite assumption is made. The infinitesimal strain theory is commonly adopted in civil and mechanical engineering for the stress analysis of structures built from relatively stiff elastic materials like concrete and steel, since a common goal in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
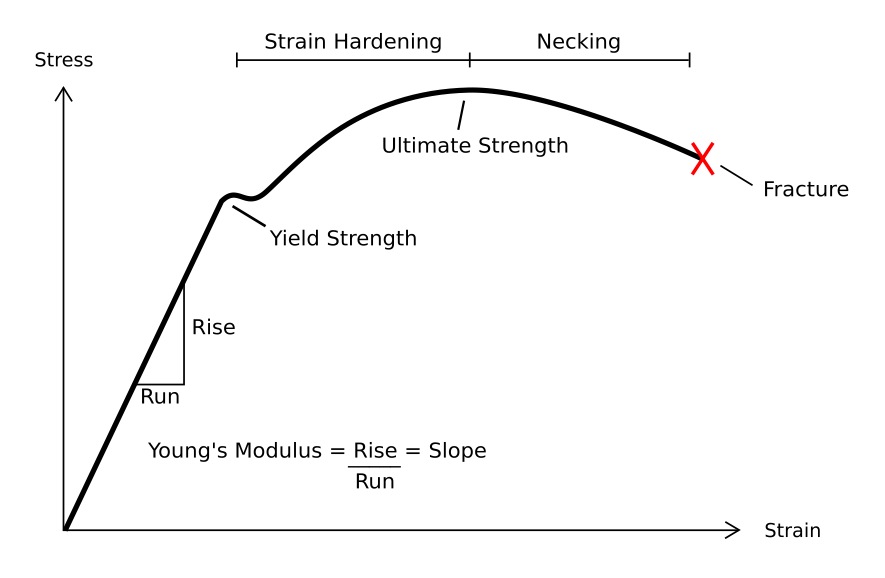
Young’s Modulus
Young's modulus E, the Young modulus, or the modulus of elasticity in tension or compression (i.e., negative tension), is a mechanical property that measures the tensile or compressive stiffness of a solid material when the force is applied lengthwise. It quantifies the relationship between tensile/compressive stress \sigma (force per unit area) and axial strain \varepsilon (proportional deformation) in the linear elastic region of a material and is determined using the formula: E = \frac Young's moduli are typically so large that they are expressed not in pascals but in gigapascals (GPa). Example: * Silly Putty (increasing pressure: length increases quickly, meaning tiny E) * Aluminum (increasing pressure: length increases slowly, meaning high E) Higher Young's modulus corresponds to greater (lengthwise) stiffness. Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first experim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Free Energy
The thermodynamic free energy is a concept useful in the thermodynamics of chemical or thermal processes in engineering and science. The change in the free energy is the maximum amount of work that a thermodynamic system can perform in a process at constant temperature, and its sign indicates whether the process is thermodynamically favorable or forbidden. Since free energy usually contains potential energy, it is not absolute but depends on the choice of a zero point. Therefore, only relative free energy values, or changes in free energy, are physically meaningful. The free energy is a thermodynamic state function, like the internal energy, enthalpy, and entropy. The free energy is the portion of any first-law energy that is available to perform thermodynamic work at constant temperature, ''i.e.'', work mediated by thermal energy. Free energy is subject to irreversible loss in the course of such work. Since first-law energy is always conserved, it is evident that free energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Energy
Elastic energy is the mechanical potential energy stored in the configuration of a material or physical system as it is subjected to elastic deformation by work performed upon it. Elastic energy occurs when objects are impermanently compressed, stretched or generally deformed in any manner. Elasticity theory primarily develops formalisms for the mechanics of solid bodies and materials. (Note however, the work done by a stretched rubber band is not an example of elastic energy. It is an example of entropic elasticity.) The elastic potential energy equation is used in calculations of positions of mechanical equilibrium. The energy is potential as it will be converted into other forms of energy, such as kinetic energy and sound energy, when the object is allowed to return to its original shape (reformation) by its elasticity. U = \frac 1 2 k\, \Delta x^2 The essence of elasticity is reversibility. Forces applied to an elastic material transfer energy into the material which, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Energy
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors. Common types of potential energy include the gravitational potential energy of an object, the elastic potential energy of an extended spring, and the electric potential energy of an electric charge in an electric field. The unit for energy in the International System of Units (SI) is the joule, which has the symbol J. The term ''potential energy'' was introduced by the 19th-century Scottish engineer and physicist William Rankine, although it has links to Greek philosopher Aristotle's concept of potentiality. Potential energy is associated with forces that act on a body in a way that the total work done by these forces on the body depends only on the initial and final positions of the body in space. These forces, that are called ''conservative forces'', can be represented at every point in space by vec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Energy
In surface science, surface free energy (also interfacial free energy or surface energy) quantifies the disruption of intermolecular bonds that occurs when a surface is created. In solid-state physics, surfaces must be intrinsically less energetically favorable than the bulk of the material (the atoms on the surface have more energy compared with the atoms in the bulk), otherwise there would be a driving force for surfaces to be created, removing the bulk of the material (see sublimation). The surface energy may therefore be defined as the excess energy at the surface of a material compared to the bulk, or it is the work required to build an area of a particular surface. Another way to view the surface energy is to relate it to the work required to cut a bulk sample, creating two surfaces. There is "excess energy" as a result of the now-incomplete, unrealized bonding at the two surfaces. Cutting a solid body into pieces disrupts its bonds and increases the surface area, and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics applies to a wide variety of topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering and mechanical engineering, but also in other complex fields such as meteorology. Historically, thermodynamics developed out of a desire to increase the efficiency of early steam engines, particularly through the work of French physicist Sadi Carnot (1824) who believed that engine efficiency was the key that could help France win the Napoleonic Wars. Scots-Irish physicist Lord Kelvin was the first to formulate a co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
