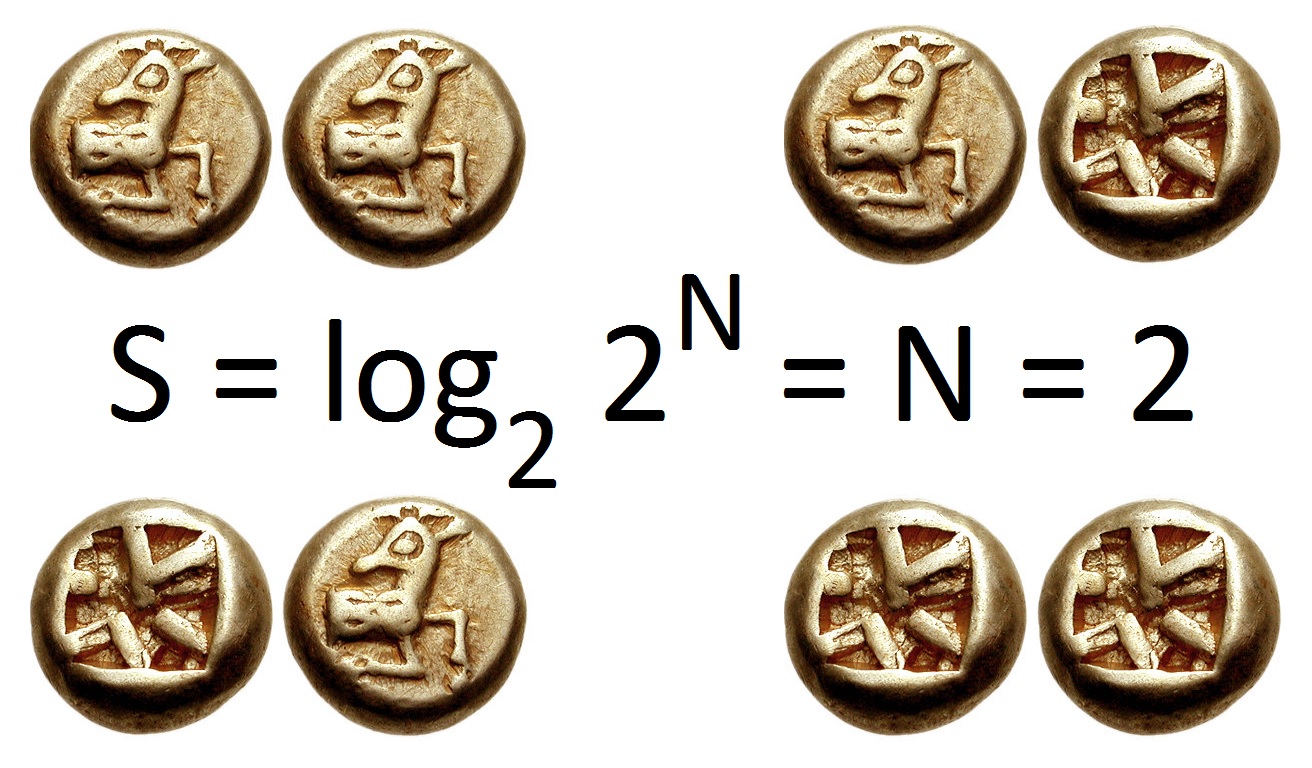|
Minkowski–Bouligand Dimension
450px, Estimating the box-counting dimension of the coast of Great Britain In fractal geometry, the Minkowski–Bouligand dimension, also known as Minkowski dimension or box-counting dimension, is a way of determining the fractal dimension of a set ''S'' in a Euclidean space R''n'', or more generally in a metric space (''X'', ''d''). It is named after the Polish mathematician Hermann Minkowski and the French mathematician Georges Bouligand. To calculate this dimension for a fractal ''S'', imagine this fractal lying on an evenly spaced grid and count how many boxes are required to cover the set. The box-counting dimension is calculated by seeing how this number changes as we make the grid finer by applying a box-counting algorithm. Suppose that ''N''(''ε'') is the number of boxes of side length ''ε'' required to cover the set. Then the box-counting dimension is defined as : \dim_\text(S) := \lim_ \frac . Roughly speaking, this means that the dimension is the exponent ''d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Britain Box
Great may refer to: Descriptions or measurements * Great, a relative measurement in physical space, see Size * Greatness, being divine, majestic, superior, majestic, or transcendent People * List of people known as "the Great" *Artel Great (born 1981), American actor Other uses * Great (1975 film), ''Great'' (1975 film), a British animated short about Isambard Kingdom Brunel * Great (2013 film), ''Great'' (2013 film), a German short film * Great (supermarket), a supermarket in Hong Kong * GReAT, Graph Rewriting and Transformation, a Model Transformation Language * Gang Resistance Education and Training, or GREAT, a school-based and police officer-instructed program * Global Research and Analysis Team (GReAT), a Kaspersky Lab#Malware_discovery, cybersecurity team at Kaspersky Lab *''Great! (EP), Great!'', a 2018 EP by Momoland *The Great (TV series), ''The Great'' (TV series), an American comedy-drama See also * * * {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Dimension
In chaos theory, the correlation dimension (denoted by ''ν'') is a measure of the dimensionality of the space occupied by a set of random points, often referred to as a type of fractal dimension. For example, if we have a set of random points on the real number line between 0 and 1, the correlation dimension will be ''ν'' = 1, while if they are distributed on say, a triangle embedded in three-dimensional space (or ''m''-dimensional space), the correlation dimension will be ''ν'' = 2. This is what we would intuitively expect from a measure of dimension. The real utility of the correlation dimension is in determining the (possibly fractional) dimensions of fractal objects. There are other methods of measuring dimension (e.g. the Hausdorff dimension, the box-counting dimension, and the information dimension) but the correlation dimension has the advantage of being straightforwardly and quickly calculated, of being less noisy when only a small number of points is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Set Condition
In fractal geometry, the open set condition (OSC) is a commonly imposed condition on self-similar fractals. In some sense, the condition imposes restrictions on the overlap in a fractal construction. Specifically, given an iterated function system of contractive mappings \psi_1, \ldots, \psi_m, the open set condition requires that there exists a nonempty, open set V satisfying two conditions: # \bigcup_^m\psi_i (V) \subseteq V, # The sets \psi_1(V), \ldots, \psi_m(V) are pairwise disjoint. Introduced in 1946 by P.A.P Moran, the open set condition is used to compute the dimensions of certain self-similar fractals, notably the Sierpinski Gasket. It is also used to simplify computation of the packing measure. An equivalent statement of the open set condition is to require that the s-dimensional Hausdorff measure of the set is greater than zero. Computing Hausdorff dimension When the open set condition holds and each \psi_i is a similitude (that is, a composition of an isometry a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hausdorff Measure
In mathematics, Hausdorff measure is a generalization of the traditional notions of area and volume to non-integer dimensions, specifically fractals and their Hausdorff dimensions. It is a type of outer measure, named for Felix Hausdorff, that assigns a number in ,∞to each set in \R^n or, more generally, in any metric space. The zero-dimensional Hausdorff measure is the number of points in the set (if the set is finite) or ∞ if the set is infinite. Likewise, the one-dimensional Hausdorff measure of a simple curve in \R^n is equal to the length of the curve, and the two-dimensional Hausdorff measure of a Lebesgue-measurable subset of \R^2 is proportional to the area of the set. Thus, the concept of the Hausdorff measure generalizes the Lebesgue measure and its notions of counting, length, and area. It also generalizes volume. In fact, there are ''d''-dimensional Hausdorff measures for any ''d'' ≥ 0, which is not necessarily an integer. These measures are fundamenta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all rational numbers, also referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by boldface , or blackboard bold \mathbb. A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real number that is not rational is called irrational. Irrational numbers include , , , and . Since the set of rational numbers is countable, and the set of real numbers is uncountable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countable Set
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (its number of elements) is not greater than that of the natural numbers. A countable set that is not finite is said countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as defined here are quite co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to , 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper "A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication. The thermodynamic concept was referred to by Scottish scientist and engineer William Rankine in 1850 with the names ''thermodynamic function'' and ''heat-potential''. In 1865, German physicist Rudolf Clausius, one of the leading founders of the field of thermodynamics, defined it as the quotient of an infinitesimal amount of hea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of is , or . The logarithm of to ''base'' is denoted as , or without parentheses, , or even without the explicit base, , when no confusion is possible, or when the base does not matter such as in big O notation. The logarithm base is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number as its base; its use is widespread in mathematics and physics, because of its very simple derivative. The binary logarithm uses base and is frequently used in computer science. Logarithms were introduced by John Napier in 1614 as a means of simplifying calculations. They were rapidly adopted by navigators, scientists, engineers, surveyors and others to perform high-a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. A geometric structure is one which defines some notion of size, distance, shape, volume, or other rigidifying structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If , , and are the lengths of the sides of the triangle, with no side being greater than , then the triangle inequality states that :z \leq x + y , with equality only in the degenerate case of a triangle with zero area. In Euclidean geometry and some other geometries, the triangle inequality is a theorem about distances, and it is written using vectors and vector lengths ( norms): :\, \mathbf x + \mathbf y\, \leq \, \mathbf x\, + \, \mathbf y\, , where the length of the third side has been replaced by the vector sum . When and are real numbers, they can be viewed as vectors in , and the trian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjoint Sets
In mathematics, two sets are said to be disjoint sets if they have no element in common. Equivalently, two disjoint sets are sets whose intersection is the empty set.. For example, and are ''disjoint sets,'' while and are not disjoint. A collection of two or more sets is called disjoint if any two distinct sets of the collection are disjoint. Generalizations This definition of disjoint sets can be extended to a family of sets \left(A_i\right)_: the family is pairwise disjoint, or mutually disjoint if A_i \cap A_j = \varnothing whenever i \neq j. Alternatively, some authors use the term disjoint to refer to this notion as well. For families the notion of pairwise disjoint or mutually disjoint is sometimes defined in a subtly different manner, in that repeated identical members are allowed: the family is pairwise disjoint if A_i \cap A_j = \varnothing whenever A_i \neq A_j (every two ''distinct'' sets in the family are disjoint).. For example, the collection of sets is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |