|
Minimal Subtraction Scheme
In quantum field theory, the minimal subtraction scheme, or MS scheme, is a particular renormalization scheme used to absorb the infinities that arise in perturbative calculations beyond leading order, introduced independently by Gerard 't Hooft and Steven Weinberg in 1973. The MS scheme consists of absorbing only the divergent part of the radiative corrections into the counterterms. In the similar and more widely used modified minimal subtraction, or MS-bar scheme (\overline), one absorbs the divergent part plus a universal constant that always arises along with the divergence in Feynman diagram calculations into the counterterms. When using dimensional regularization, i.e. d^4 p \to \mu^ d^d p, it is implemented by rescaling the renormalization scale: \mu^2 \to \mu^2 \frac, with \gamma_ the Euler–Mascheroni constant Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma () ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. QFT treats particles as excited states (also called Quantum, quanta) of their underlying quantum field (physics), fields, which are more fundamental than the particles. The equation of motion of the particle is determined by minimization of the Lagrangian, a functional of fields associated with the particle. Interactions between particles are described by interaction terms in the Lagrangian (field theory), Lagrangian involving their corresponding quantum fields. Each interaction can be visually represented by Feynman diagrams according to perturbation theory (quantum mechanics), perturbation theory in quantum mechanics. History Quantum field theory emerged from the wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Renormalization
Renormalization is a collection of techniques in quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian. For example, an electron theory may begin by postulating an electron with an initial mass and charge. In quantum field theory a cloud of virtual particles, such as photons, positrons, and others surrounds and interacts with the initial electron. Accounting for the interactions of the surrounding particles (e.g. collisions at different energies) shows that the electron-system behaves as if it had a different mass and charge than initially postulated. Renormalization, in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leading-order
The leading-order terms (or corrections) within a mathematical equation, expression or model are the terms with the largest order of magnitude.J.K.Hunter, ''Asymptotic Analysis and Singular Perturbation Theory'', 2004. http://www.math.ucdavis.edu/~hunter/notes/asy.pdf The sizes of the different terms in the equation(s) will change as the variables change, and hence, which terms are leading-order may also change. A common and powerful way of simplifying and understanding a wide variety of complicated mathematical models is to investigate which terms are the largest (and therefore most important), for particular sizes of the variables and parameters, and analyse the behaviour produced by just these terms (regarding the other smaller terms as negligible). This gives the main behaviour – the true behaviour is only small deviations away from this. This main behaviour may be captured sufficiently well by just the strictly leading-order terms, or it may be decided that slightly smaller ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gerard 't Hooft
Gerardus (Gerard) 't Hooft (; born July 5, 1946) is a Dutch theoretical physicist and professor at Utrecht University, the Netherlands. He shared the 1999 Nobel Prize in Physics with his thesis advisor Martinus J. G. Veltman "for elucidating the quantum structure of electroweak interactions". His work concentrates on gauge theory, black holes, quantum gravity and fundamental aspects of quantum mechanics. His contributions to physics include a proof that gauge theories are renormalizable, dimensional regularization and the holographic principle. Personal life He is married to Albertha Schik (Betteke) and has two daughters, Saskia and Ellen. Biography Early life Gerard 't Hooft was born in Den Helder on July 5, 1946, but grew up in The Hague. He was the middle child of a family of three. He comes from a family of scholars. His great uncle was Nobel prize laureate Frits Zernike, and his grandmother was married to Pieter Nicolaas van Kampen, a professor of zoology at Leiden Uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steven Weinberg
Steven Weinberg (; May 3, 1933 – July 23, 2021) was an American theoretical physicist and Nobel laureate in physics for his contributions with Abdus Salam and Sheldon Glashow to the unification of the weak force and electromagnetic interaction between elementary particles. He held the Josey Regental Chair in Science at the University of Texas at Austin, where he was a member of the Physics and Astronomy Departments. His research on elementary particles and physical cosmology was honored with numerous prizes and awards, including the 1979 Nobel Prize in physics and the 1991 National Medal of Science. In 2004, he received the Benjamin Franklin Medal of the American Philosophical Society, with a citation that said he was "considered by many to be the preeminent theoretical physicist alive in the world today." He was elected to the U.S. National Academy of Sciences, Britain's Royal Society, the American Philosophical Society, and the American Academy of Arts and Sciences. Weinb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nuclear Physics B
Nuclear may refer to: Physics Relating to the nucleus of the atom: *Nuclear engineering *Nuclear physics *Nuclear power Nuclear power is the use of nuclear reactions to produce electricity. Nuclear power can be obtained from nuclear fission, nuclear decay and nuclear fusion reactions. Presently, the vast majority of electricity from nuclear power is produced b ... *Nuclear reactor *Nuclear weapon *Nuclear medicine *Radiation therapy *Nuclear warfare Mathematics *Nuclear space *Nuclear operator *Nuclear congruence *Nuclear C*-algebra Biology Relating to the Cell nucleus, nucleus of the cell: * Nuclear DNA Society *Nuclear family, a family consisting of a pair of adults and their children Music *Nuclear (band), "Nuclear" (band), group music. *Nuclear (Ryan Adams song), "Nuclear" (Ryan Adams song), 2002 *"Nuclear", a song by Mike Oldfield from his ''Man on the Rocks'' album *Nu.Clear (EP), ''Nu.Clear'' (EP) by South Korean girl group CLC See also *Nucleus (disambigu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Review D
Physical may refer to: *Physical examination In a physical examination, medical examination, or clinical examination, a medical practitioner examines a patient for any possible medical signs or symptoms of a medical condition. It generally consists of a series of questions about the pati ..., a regular overall check-up with a doctor * ''Physical'' (Olivia Newton-John album), 1981 ** "Physical" (Olivia Newton-John song) * ''Physical'' (Gabe Gurnsey album) * "Physical" (Alcazar song) (2004) * "Physical" (Enrique Iglesias song) (2014) * "Physical" (Dua Lipa song) (2020) *"Physical (You're So)", a 1980 song by Adam & the Ants, the B side to " Dog Eat Dog" * ''Physical'' (TV series), an American television series See also {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Counterterm
Renormalization is a collection of techniques in quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian. For example, an electron theory may begin by postulating an electron with an initial mass and charge. In quantum field theory a cloud of virtual particles, such as photons, positrons, and others surrounds and interacts with the initial electron. Accounting for the interactions of the surrounding particles (e.g. collisions at different energies) shows that the electron-system behaves as if it had a different mass and charge than initially postulated. Renormalization, in thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feynman Diagram
In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced the diagrams in 1948. The interaction of subatomic particles can be complex and difficult to understand; Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. According to David Kaiser, "Since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations. Feynman diagrams have revolutionized nearly every aspect of theoretical physics." While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory. Frank Wilczek wrote that the calculations that won him the 2004 Nobel Prize in Physics "would have been literally unthinkable without Feynman diagra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensional Regularization
__NOTOC__ In theoretical physics, dimensional regularization is a method introduced by Giambiagi and Bollini as well as – independently and more comprehensively – by 't Hooft and Veltman for regularizing integrals in the evaluation of Feynman diagrams; in other words, assigning values to them that are meromorphic functions of a complex parameter ''d'', the analytic continuation of the number of spacetime dimensions. Dimensional regularization writes a Feynman integral as an integral depending on the spacetime dimension ''d'' and the squared distances (''x''''i''−''x''''j'')2 of the spacetime points ''x''''i'', ... appearing in it. In Euclidean space, the integral often converges for −Re(''d'') sufficiently large, and can be analytically continued from this region to a meromorphic function defined for all complex ''d''. In general, there will be a pole at the physical value (usually 4) of ''d'', which needs to be canceled by renormalization to obtain physical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
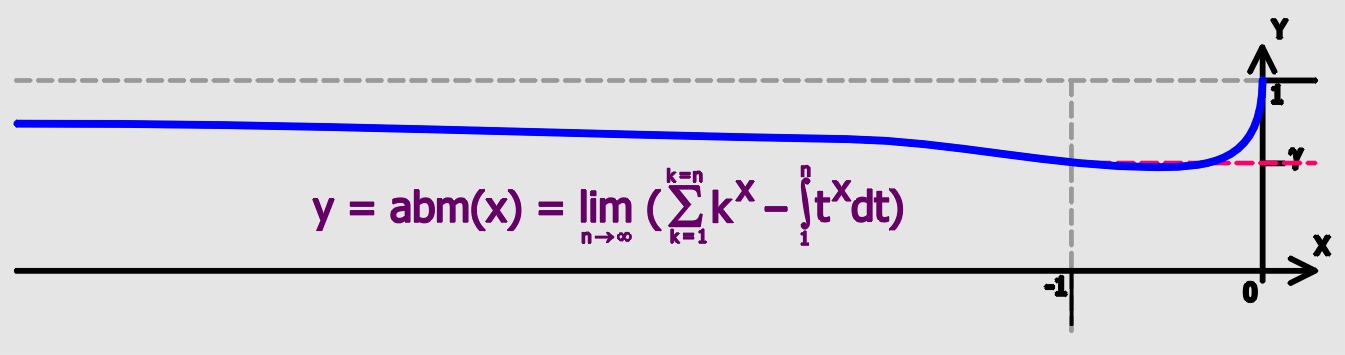
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press A university press is an academic publishing house specializing in monographs and scholarly journals. Most are nonprofit organizations and an integral component of a large research university. They publish work that has been reviewed by schola ... in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |