|
Microscale And Macroscale Models
Microscale models form a broad class of computational models that simulate fine-scale details, in contrast with macroscale models, which amalgamate details into select categories. Microscale and macroscale models can be used together to understand different aspects of the same problem. Applications Macroscale models can include ordinary, partial, and integro-differential equations, where categories and flows between the categories determine the dynamics, or may involve only algebraic equations. An abstract macroscale model may be combined with more detailed microscale models. Connections between the two scales are related to multiscale modeling. One mathematical technique for multiscale modeling of nanomaterials is based upon the use of multiscale Green's function. In contrast, microscale models can simulate a variety of details, such as individual bacteria in biofilms, individual pedestrians in simulated neighborhoods, individual light beams in ray-tracing imagery, indi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Chemical Basis Of Morphogenesis
"The Chemical Basis of Morphogenesis" is an article that the English mathematician Alan Turing wrote in 1952. It describes how patterns in nature, such as stripes and spirals, can arise naturally from a homogeneous, uniform state. The theory, which can be called a reaction–diffusion theory of morphogenesis, has become a basic model in theoretical biology. Such patterns have come to be known as Turing patterns. For example, it has been postulated that the protein VEGFC can form Turing patterns to govern the formation of lymphatic vessels in the zebrafish embryo. Reaction–diffusion systems Reaction–diffusion systems have attracted much interest as a prototype model for pattern formation. Patterns such as fronts, spirals, targets, hexagons, stripes and dissipative solitons are found in various types of reaction-diffusion systems in spite of large discrepancies e.g. in the local reaction terms. Such patterns have been dubbed "Turing patterns". Reaction–diffusion proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
National Ecological Observatory Network
National Ecological Observatory Network (NEON) is a large facility program operated by Battelle Memorial Institute and funded by the National Science Foundation. In full operation since 2019, NEON gathers and provides long-term, standardized data on ecological responses of the biosphere to changes in land use and climate, and on feedback with the geosphere, hydrosphere, and atmosphere. NEON is a continental-scale research platform for understanding how and why our ecosystems are changing. Vision and mission The vision for NEON is to guide global understanding and decisions in a changing environment with scientific information about continental-scale ecology through integrated observations, experiments and forecasts. NEON's mission is to design, implement and operate the first and foremost integrated continental‐scale scientific infrastructure to enable research, discovery and education about ecological change. NEON collects ecological and climatic observations across the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
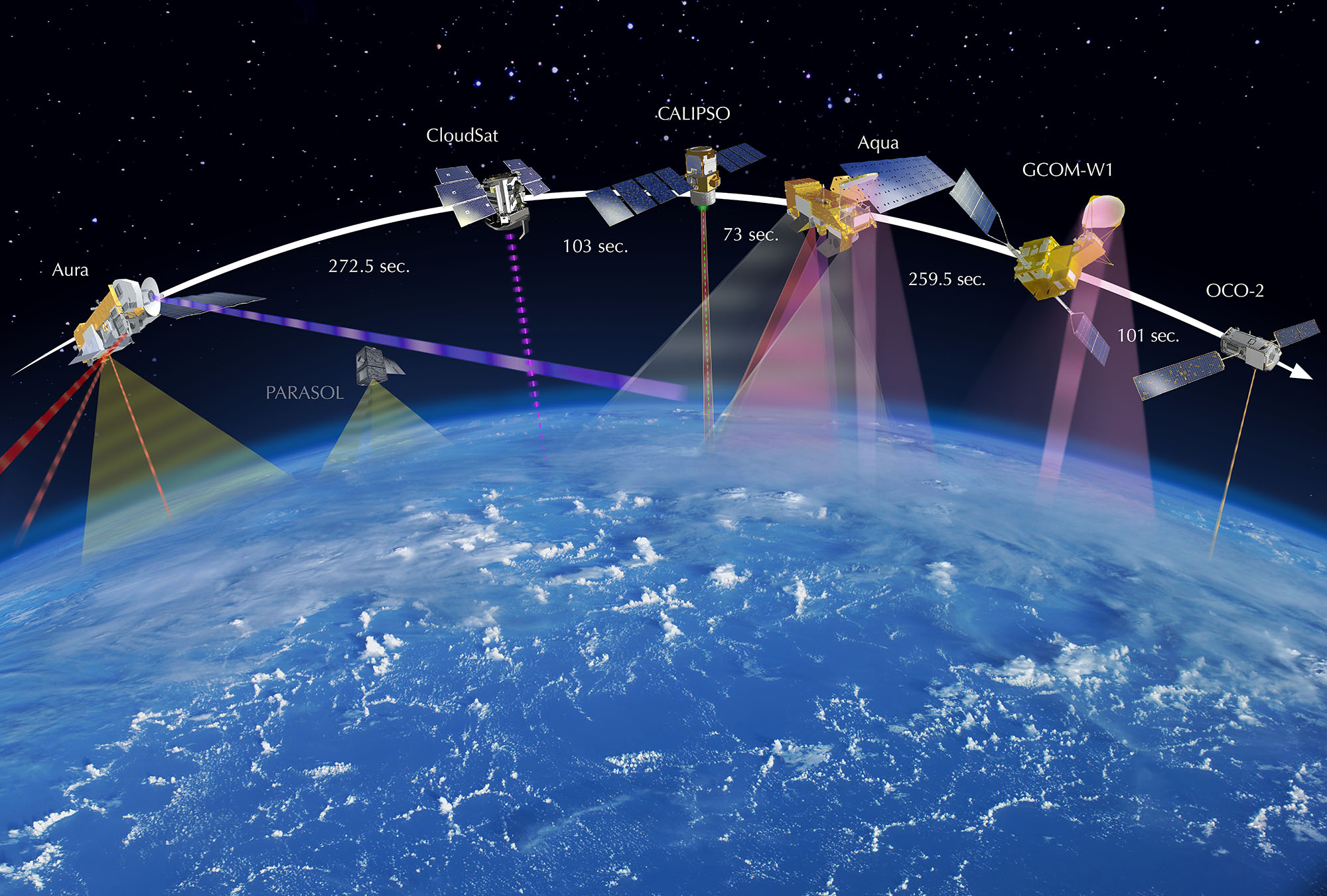
Earth Observation Satellite
An Earth observation satellite or Earth remote sensing satellite is a satellite used or designed for Earth observation (EO) from orbit, including spy satellites and similar ones intended for non-military uses such as environmental monitoring, meteorology, cartography and others. The most common type are Earth imaging satellites, that take satellite images, analogous to aerial photographs; some EO satellites may perform remote sensing without forming pictures, such as in GNSS radio occultation. The first occurrence of satellite remote sensing can be dated to the launch of the first artificial satellite, Sputnik 1, by the Soviet Union on October 4, 1957. Sputnik 1 sent back radio signals, which scientists used to study the ionosphere. The United States Army Ballistic Missile Agency launched the first American satellite, Explorer 1, for NASA’s Jet Propulsion Laboratory on January 31, 1958. The information sent back from its radiation detector led to the discovery of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Method
In mathematics and computational science, the Euler method (also called forward Euler method) is a first-order numerical procedure for solving ordinary differential equations (ODEs) with a given initial value. It is the most basic explicit method for numerical integration of ordinary differential equations and is the simplest Runge–Kutta method. The Euler method is named after Leonhard Euler, who treated it in his book '' Institutionum calculi integralis'' (published 1768–1870). The Euler method is a first-order method, which means that the local error (error per step) is proportional to the square of the step size, and the global error (error at a given time) is proportional to the step size. The Euler method often serves as the basis to construct more complex methods, e.g., predictor–corrector method. Informal geometrical description Consider the problem of calculating the shape of an unknown curve which starts at a given point and satisfies a given differential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation-free Modeling
Equation-free modeling is a method for multiscale computation and computer-aided analysis. It is designed for a class of complicated systems in which one observes evolution at a macroscopic, coarse scale of interest, while accurate models are only given at a finely detailed, microscopic, level of description. The framework empowers one to perform macroscopic computational tasks (over large space-time scales) using only appropriately initialized microscopic simulation on short time and small length scales. The methodology eliminates the derivation of explicit macroscopic evolution equations when these equations conceptually exist but are not available in closed form; hence the term equation-free. Introduction In a wide range of chemical, physical and biological systems, coherent macroscopic behavior emerges from interactions between microscopic entities themselves (molecules, cells, grains, animals in a population, agents) and with their environment. Sometimes, remarkably, a coarse- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's laws of diffusion). In mathematics, it is related to Markov processes, such as random walks, and applied in many other fields, such as materials science, information theory, and biophysics. The diffusion equation is a special case of the convection–diffusion equation, when bulk velocity is zero. It is equivalent to the heat equation under some circumstances. Statement The equation is usually written as: where is the density of the diffusing material at location and time and is the collective diffusion coefficient for density at location ; and represents the vector differential operator del. If the diffusion coefficient depends on the density then the equation is nonlinear, otherwise it is linear. The equation above applies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Decay
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where is the quantity and (lambda) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant: :\frac = -\lambda N. The solution to this equation (see derivation below) is: :N(t) = N_0 e^, where is the quantity at time , is the initial quantity, that is, the quantity at time . Measuring rates of decay Mean lifetime If the decaying quantity, ''N''(''t''), is the number of discrete elements in a certain set, it is possible to compute the average length of time that an element remains in the set. This is called the mean lifetime (or simply the lifetime), where the exponential time constant, \tau, relates to the decay rate constant, λ, in the following way: :\tau = \frac. The mean lifetime can be looked at a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capital (economics)
In economics, capital goods or capital are "those durable produced goods that are in turn used as productive inputs for further production" of goods and services. At the macroeconomic level, "the nation's capital stock includes buildings, equipment, software, and inventories during a given year." A typical example is the machinery used in factories. Capital can be increased by the use of the factors of production, which however excludes certain durable goods like homes and personal automobiles that are not used in the production of saleable goods and services. Adam Smith defined capital as "that part of man's stock which he expects to afford him revenue". In economic models, capital is an input in the production function. The total physical capital at any given moment in time is referred to as the capital stock (not to be confused with the capital stock of a business entity). Capital goods, real capital, or capital assets are already-produced, durable goods or any n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Growth
Exponential growth is a process that increases quantity over time. It occurs when the instantaneous rate of change (that is, the derivative) of a quantity with respect to time is proportional to the quantity itself. Described as a function, a quantity undergoing exponential growth is an exponential function of time, that is, the variable representing time is the exponent (in contrast to other types of growth, such as quadratic growth). If the constant of proportionality is negative, then the quantity decreases over time, and is said to be undergoing exponential decay instead. In the case of a discrete domain of definition with equal intervals, it is also called geometric growth or geometric decay since the function values form a geometric progression. The formula for exponential growth of a variable at the growth rate , as time goes on in discrete intervals (that is, at integer times 0, 1, 2, 3, ...), is x_t = x_0(1+r)^t where is the value of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moore's Law
Moore's law is the observation that the number of transistors in a dense integrated circuit (IC) doubles about every two years. Moore's law is an observation and projection of a historical trend. Rather than a law of physics, it is an empirical relationship linked to gains from experience in production. The observation is named after Gordon Moore, the co-founder of Fairchild Semiconductor and Intel (and former CEO of the latter), who in 1965 posited a doubling every year in the number of components per integrated circuit, and projected this rate of growth would continue for at least another decade. In 1975, looking forward to the next decade, he revised the forecast to doubling every two years, a compound annual growth rate (CAGR) of 41%. While Moore did not use empirical evidence in forecasting that the historical trend would continue, his prediction held since 1975 and has since become known as a "law". Moore's prediction has been used in the semiconductor industry t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |