|
Mechanical Impedance
Mechanical impedance is a measure of how much a structure resists motion when subjected to a harmonic force. It relates forces with velocities acting on a mechanical system. The mechanical impedance of a point on a structure is the ratio of the force applied at a point to the resulting velocity at that point. Mechanical impedance is the inverse of mechanical admittance or mobility. The mechanical impedance is a function of the frequency \omega of the applied force and can vary greatly over frequency. At resonant frequencies, the mechanical impedance will be lower, meaning less force is needed to cause a structure to move at a given velocity. A simple example of this is pushing a child on a swing. For the greatest swing amplitude, the frequency of the pushes must be near the resonant frequency of the system. \mathbf(\omega) = \mathbf(\omega)\mathbf(\omega) Where, \mathbf is the force vector, \mathbf is the velocity vector, \mathbf is the impedance matrix and \omega is the angular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Admittance
In electrical engineering, admittance is a measure of how easily a circuit or device will allow a current to flow. It is defined as the reciprocal of impedance, analogous to how conductance & resistance are defined. The SI unit of admittance is the siemens (symbol S); the older, synonymous unit is mho, and its symbol is ℧ (an upside-down uppercase omega Ω). Oliver Heaviside coined the term ''admittance'' in December 1887. Heaviside used ''Y'' to represent the magnitude of admittance, but it quickly became the conventional symbol for admittance itself through the publications of Charles Proteus Steinmetz. Heaviside probably chose ''Y'' simply because it is next to ''Z'' in the alphabet, the conventional symbol for impedance. Admittance is defined as :Y \equiv \frac \, where :''Y'' is the admittance, measured in siemens :''Z'' is the impedance, measured in ohms Resistance is a measure of the opposition of a circuit to the flow of a steady current, while impedanc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
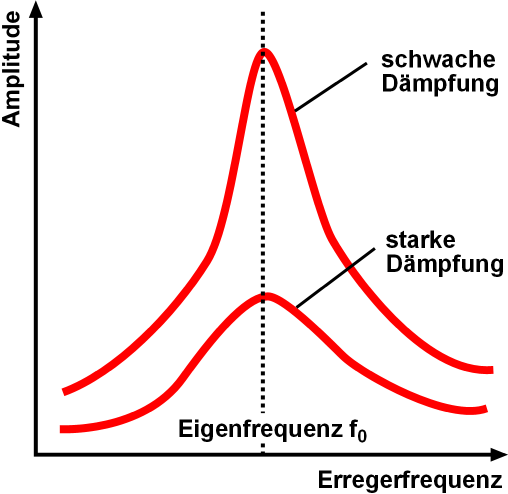
Resonant
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Potential
In mathematical physics, scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value ( scalar) that depends only on its location. A familiar example is potential energy due to gravity. A ''scalar potential'' is a fundamental concept in vector analysis and physics (the adjective ''scalar'' is frequently omitted if there is no danger of confusion with '' vector potential''). The scalar potential is an example of a scalar field. Given a vector field , the scalar potential is defined such that: : \mathbf = -\nabla P = - \left( \frac, \frac, \frac \right), where is the gradient of and the second part of the equation is minus the gradient for a function of the Cartesian coordinates . In some cases, mathematicians may us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustic Impedance
Acoustic impedance and specific acoustic impedance are measures of the opposition that a system presents to the acoustic flow resulting from an acoustic pressure applied to the system. The SI unit of acoustic impedance is the pascal-second per cubic metre (), or in the MKS system the rayl per square metre (), while that of specific acoustic impedance is the pascal-second per metre (), or in the MKS system the rayl. There is a close analogy with electrical impedance, which measures the opposition that a system presents to the electric current resulting from a voltage applied to the system. Mathematical definitions Acoustic impedance For a linear time-invariant system, the relationship between the acoustic pressure applied to the system and the resulting acoustic volume flow rate through a surface perpendicular to the direction of that pressure at its point of application is given by: : p(t) = * Qt), or equivalently by : Q(t) = * pt), where * ''p'' is the acoustic pressure; * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Response
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of systems, such as audio and control systems, where they simplify mathematical analysis by converting governing differential equations into algebraic equations. In an audio system, it may be used to minimize audible distortion by designing components (such as microphones, amplifiers and loudspeakers) so that the overall response is as flat (uniform) as possible across the system's bandwidth. In control systems, such as a vehicle's cruise control, it may be used to assess system stability, often through the use of Bode plots. Systems with a specific frequency response can be designed using analog and digital filters. The frequency response characterizes systems in the frequency domain, just as the impulse response characterizes systems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Impedance Analogy
The impedance analogy is a method of representing a mechanical system by an analogous electrical system. The advantage of doing this is that there is a large body of theory and analysis techniques concerning complex electrical systems, especially in the field of filters. By converting to an electrical representation, these tools in the electrical domain can be directly applied to a mechanical system without modification. A further advantage occurs in electromechanical systems: Converting the mechanical part of such a system into the electrical domain allows the entire system to be analysed as a unified whole. The mathematical behaviour of the simulated electrical system is identical to the mathematical behaviour of the represented mechanical system. Each element in the electrical domain has a corresponding element in the mechanical domain with an analogous constitutive equation. All laws of circuit analysis, such as Kirchhoff's circuit laws, that apply in the electrical doma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Response Function
A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response. Because of its many applications in information theory, physics and engineering there exist alternative names for specific linear response functions such as susceptibility, impulse response or impedance, see also transfer function. The concept of a Green's function or fundamental solution of an ordinary differential equation is closely related. Mathematical definition Denote the input of a system by h(t) (e.g. a force), and the response of the system by x(t) (e.g. a position). Generally, the value of x(t) will depend not only on the present value of h(t), but also on past values. Approximately x(t) is a weighted sum of the previous values of h(t'), with the weights given by the linear response function \chi(t-t'): x(t) = \int_^t dt'\, \chi(t-t') h(t') + \cdots\,. The explicit term on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |