|
Maxwell–Boltzmann Statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density is low enough to render quantum effects negligible. The expected number of particles with energy \varepsilon_i for Maxwell–Boltzmann statistics is :\langle N_i \rangle = \frac = \frac\,g_i e^, where: *\varepsilon_i is the energy of the ''i''-th energy level, *\langle N_i \rangle is the average number of particles in the set of states with energy \varepsilon_i, *g_i is the degeneracy of energy level ''i'', that is, the number of states with energy \varepsilon_i which may nevertheless be distinguished from each other by some other means,For example, two simple point particles may have the same energy, but different momentum vectors. They may be distinguished from each other on this basis, and the degeneracy will be the number of poss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Statistics
Particle statistics is a particular description of multiple particles in statistical mechanics. A key prerequisite concept is that of a statistical ensemble (an idealization comprising the state space of possible states of a system, each labeled with a probability) that emphasizes properties of a large system as a whole at the expense of knowledge about parameters of separate particles. When an ensemble describes a system of particles with similar properties, their number is called the particle number and usually denoted by ''N''. Classical statistics In classical mechanics, all particles ( fundamental and composite particles, atoms, molecules, electrons, etc.) in the system are considered distinguishable. This means that individual particles in a system can be tracked. As a consequence, switching the positions of any pair of particles in the system leads to a different configuration of the system. Furthermore, there is no restriction on placing more than one particle in any giv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Paradox
In statistical mechanics, a semi-classical derivation of entropy that does not take into account the indistinguishability of particles yields an expression for entropy which is not extensive (is not proportional to the amount of substance in question). This leads to a paradox known as the Gibbs paradox, after Josiah Willard Gibbs, who proposed this thought experiment in 1874‒1875. The paradox allows for the entropy of closed systems to decrease, violating the second law of thermodynamics. A related paradox is the "mixing paradox". If one takes the perspective that the definition of entropy must be changed so as to ignore particle permutation, in the thermodynamic limit, the paradox is averted. Illustration of the problem Gibbs himself considered the following problem that arises if the ideal gas entropy is not extensive. Reprinted in and in Two identical containers of an ideal gas sit side-by-side. The gas in container #1 is identical in every respect to the gas i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication. The thermodynamic concept was referred to by Scottish scientist and engineer William Rankine in 1850 with the names ''thermodynamic function'' and ''heat-potential''. In 1865, German physicist Rudolf Clausius, one of the leading founders of the field of thermodynamics, defined it as the quotient of an infinitesimal amount ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ludwig Boltzmann
Ludwig Eduard Boltzmann (; 20 February 1844 – 5 September 1906) was an Austrian physicist and philosopher. His greatest achievements were the development of statistical mechanics, and the statistical explanation of the second law of thermodynamics. In 1877 he provided the current definition of entropy, S = k_ \ln \Omega \!, where Ω is the number of microstates whose energy equals the system's energy, interpreted as a measure of statistical disorder of a system. Max Planck named the constant the Boltzmann constant. Statistical mechanics is one of the pillars of modern physics. It describes how macroscopic observations (such as temperature and pressure) are related to microscopic parameters that fluctuate around an average. It connects thermodynamic quantities (such as heat capacity) to microscopic behavior, whereas, in classical thermodynamics, the only available option would be to measure and tabulate such quantities for various materials. Biography Childhood and educat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multinomial Coefficient
In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials. Theorem For any positive integer and any non-negative integer , the multinomial formula describes how a sum with terms expands when raised to an arbitrary power : :(x_1 + x_2 + \cdots + x_m)^n = \sum_ \prod_^m x_t^\,, where : = \frac is a multinomial coefficient. The sum is taken over all combinations of nonnegative integer indices through such that the sum of all is . That is, for each term in the expansion, the exponents of the must add up to . Also, as with the binomial theorem, quantities of the form that appear are taken to equal 1 ( even when equals zero). In the case , this statement reduces to that of the binomial theorem. Example The third power of the trinomial is given by :(a+b+c)^3 = a^3 + b^3 + c^3 + 3 a^2 b + 3 a^2 c + 3 b^2 a + 3 b^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combination
In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter (unlike permutations). For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a ''k''-combination of a set ''S'' is a subset of ''k'' distinct elements of ''S''. So, two combinations are identical if and only if each combination has the same members. (The arrangement of the members in each set does not matter.) If the set has ''n'' elements, the number of ''k''-combinations, denoted as C^n_k, is equal to the binomial coefficient \binom nk = \frac, which can be written using factorials as \textstyle\frac whenever k\leq n, and which is zero when k>n. This formula can be derived from the fact that each ''k''-combination of a set ''S'' of ''n'' members has k! permutations so P^n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lottery
A lottery is a form of gambling that involves the drawing of numbers at random for a prize. Some governments outlaw lotteries, while others endorse it to the extent of organizing a national or state lottery. It is common to find some degree of regulation of lottery by governments. The most common regulation is prohibition of sale to minors, and vendors must be licensed to sell lottery tickets. Although lotteries were common in the United States and some other countries during the 19th century, by the beginning of the 20th century, most forms of gambling, including lotteries and sweepstakes, were illegal in the U.S. and most of Europe as well as many other countries. This remained so until well after World War II. In the 1960s, casinos and lotteries began to re-appear throughout the world as a means for governments to raise revenue without raising taxes. Lotteries come in many formats. For example, the prize can be a fixed amount of cash or goods. In this format, there is ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Microcanonical Ensemble
In statistical mechanics, the microcanonical ensemble is a statistical ensemble that represents the possible states of a mechanical system whose total energy is exactly specified. The system is assumed to be isolated in the sense that it cannot exchange energy or particles with its environment, so that (by conservation of energy) the energy of the system does not change with time. The primary macroscopic variables of the microcanonical ensemble are the total number of particles in the system (symbol: ), the system's volume (symbol: ), as well as the total energy in the system (symbol: ). Each of these is assumed to be constant in the ensemble. For this reason, the microcanonical ensemble is sometimes called the ensemble. In simple terms, the microcanonical ensemble is defined by assigning an equal probability to every microstate whose energy falls within a range centered at . All other microstates are given a probability of zero. Since the probabilities must add up to 1, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Ensemble
In statistical mechanics, a canonical ensemble is the statistical ensemble that represents the possible states of a mechanical system in thermal equilibrium with a heat bath at a fixed temperature. The system can exchange energy with the heat bath, so that the states of the system will differ in total energy. The principal thermodynamic variable of the canonical ensemble, determining the probability distribution of states, is the absolute temperature (symbol: ). The ensemble typically also depends on mechanical variables such as the number of particles in the system (symbol: ) and the system's volume (symbol: ), each of which influence the nature of the system's internal states. An ensemble with these three parameters is sometimes called the ensemble. The canonical ensemble assigns a probability to each distinct microstate given by the following exponential: :P = e^, where is the total energy of the microstate, and is the Boltzmann constant. The number is the free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grand Canonical Ensemble
In statistical mechanics, the grand canonical ensemble (also known as the macrocanonical ensemble) is the statistical ensemble that is used to represent the possible states of a mechanical system of particles that are in thermodynamic equilibrium (thermal and chemical) with a reservoir. The system is said to be open in the sense that the system can exchange energy and particles with a reservoir, so that various possible states of the system can differ in both their total energy and total number of particles. The system's volume, shape, and other external coordinates are kept the same in all possible states of the system. The thermodynamic variables of the grand canonical ensemble are chemical potential (symbol: ) and absolute temperature (symbol: . The ensemble is also dependent on mechanical variables such as volume (symbol: which influence the nature of the system's internal states. This ensemble is therefore sometimes called the ensemble, as each of these three quantitie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dover Publications
Dover Publications, also known as Dover Books, is an American book publisher founded in 1941 by Hayward and Blanche Cirker. It primarily reissues books that are out of print from their original publishers. These are often, but not always, books in the public domain. The original published editions may be scarce or historically significant. Dover republishes these books, making them available at a significantly reduced cost. Classic reprints Dover reprints classic works of literature, classical sheet music, and public-domain images from the 18th and 19th centuries. Dover also publishes an extensive collection of mathematical, scientific, and engineering texts. It often targets its reprints at a niche market, such as woodworking. Starting in 2015, the company branched out into graphic novel reprints, overseen by Dover acquisitions editor and former comics writer and editor Drew Ford. Most Dover reprints are photo facsimiles of the originals, retaining the original pagination an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
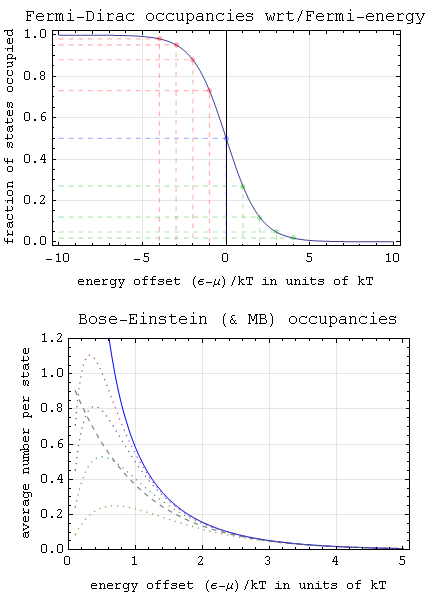
Fermi–Dirac Statistics
Fermi–Dirac statistics (F–D statistics) is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926 (although Fermi derived it before Dirac). Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics. F–D statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the F–D distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |