|
Matsubara Frequency
In thermal quantum field theory, the Matsubara frequency summation (named after Takeo Matsubara) is a technique used to simplify calculations involving Euclidean (imaginary time) path integrals. In thermal quantum field theory, bosonic and fermionic quantum fields \phi(\tau) are respectively periodic or antiperiodic in imaginary time \tau, with periodicity \beta = \hbar / k_ T. Matsubara summation refers to the technique of expanding these fields in Fourier series \phi(\tau) = \frac\sum_ e^\phi(i\omega_n) \iff \phi(i\omega_n) = \frac \int_0^\beta d\tau\ e^\phi(\tau). The frequencies \omega_n are called the Matsubara frequencies, taking values from either of the following sets (with n\in\mathbb): *bosonic frequencies: \omega_n=\frac, *fermionic frequencies: \omega_n=\frac, which respectively enforce periodic and antiperiodic boundary conditions on the field \phi(\tau). Once such substitutions have been made, certain diagrams contributing to the action take the form of a so-ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Quantum Field Theory
In theoretical physics, thermal quantum field theory (thermal field theory for short) or finite temperature field theory is a set of methods to calculate expectation values of physical observables of a quantum field theory at finite temperature. In the Matsubara formalism, the basic idea (due to Felix Bloch) is that the expectation values of operators in a canonical ensemble : \langle A\rangle=\frac may be written as expectation values in ordinary quantum field theory where the configuration is evolved by an imaginary time \tau = i t(0\leq\tau\leq\beta). One can therefore switch to a spacetime with Euclidean signature, where the above trace (Tr) leads to the requirement that all bosonic and fermionic fields be periodic and antiperiodic, respectively, with respect to the Euclidean time direction with periodicity \beta = 1/(kT) (we are assuming natural units \hbar = 1). This allows one to perform calculations with the same tools as in ordinary quantum field theory, such as func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Takeo Matsubara
was a Japanese physicist. Matsubara proposed a method of statistical mechanics related to Green's function (many-body theory), by applying quantum field theory techniques to statistical physics. This method, commonly known as Matsubara Green's function technique, introduces the notion of imaginary time, and the reciprocal variable to this imaginary time is known as discrete Matsubara frequency. Matsubara graduated from Osaka Imperial University, and worked as full professor in Hokkaido University, Kyoto University, and Okayama University of Science. He was the winner of the Nishina Memorial Prize in 1961, and took the directorship of the Physical Society of Japan. His work with Yukata Toyozawa on impurity bands in semiconductor A semiconductor is a material with electrical conductivity between that of a conductor and an insulator. Its conductivity can be modified by adding impurities (" doping") to its crystal structure. When two regions with different doping level .. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path Integral Formulation
The path integral formulation is a description in quantum mechanics that generalizes the stationary action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude. This formulation has proven crucial to the subsequent development of theoretical physics, because manifest Lorentz covariance (time and space components of quantities enter equations in the same way) is easier to achieve than in the operator formalism of canonical quantization. Unlike previous methods, the path integral allows one to easily change coordinates between very different canonical descriptions of the same quantum system. Another advantage is that it is in practice easier to guess the correct form of the Lagrangian of a theory, which naturally enters the path integrals (for interactions of a certain type, these ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexei Alekseyevich Abrikosov
Alexei Alexeyevich Abrikosov (; June 25, 1928 – March 29, 2017) was a Soviet, Russian and AmericanAlexei A. AbrikosovAutobiography Nobelprize.org, the official website of the Nobel Prize, 2003 theoretical physicist whose main contributions are in the field of condensed matter physics. He was the co-recipient of the 2003 Nobel Prize in Physics, with Vitaly Ginzburg and Anthony James Leggett, for theories about how matter can behave at extremely low temperatures. Education and early life Abrikosov was born in Moscow, Russian SFSR, Soviet Union, on June 25, 1928, to a couple of physicians: Aleksey Abrikosov and Fani ( Wulf). His mother was Jewish. After graduating from high school in 1943, Abrikosov began studying energy technology. He graduated from Moscow State University in 1948. From 1948 to 1965, he worked at the Institute for Physical Problems of the USSR Academy of Sciences, where he received his Ph.D. in 1951 for the theory of thermal diffusion in plasmas, and then h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lev Gor'kov
Lev Petrovich Gor'kov (; 14 June 1929 – 28 December 2016) was a Russian-American research physicist internationally known for his pioneering work in the field of superconductivity. He was particularly famous for developing microscopic foundations of the Ginzburg–Landau theory of superconductivity ( Vitaly Ginzburg was awarded the 2003 Nobel prize in physics for developing, together with Lev Landau, that phenomenological theory). Gor'kov was a professor of physics at Florida State University in Tallahassee, Florida, and a program director in Condensed Matter at the National High Magnetic Field Laboratory. He was one of the Magnet Lab's founding scientists. Biography Gor'kov was born in Moscow and received his academic training when he was at Moscow State University, after which he entered Kapitza Institute for Physical Problems, and eventually joined the Landau Institute for Theoretical Physics. In 1966, he was awarded the Lenin Prize, Russia's highest award for scientific a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Igor Dzyaloshinskii
Igor Ekhielevich Dzyaloshinskii, (Игорь Ехиельевич Дзялошинский, surname sometimes transliterated as Dzyaloshinsky, Dzyaloshinski, Dzyaloshinskiĭ, or Dzyaloshinkiy, 1February 193114July 2021) was a Russian theoretical physicist, known for his research on "magnetism, multiferroics, one-dimensional conductors, liquid crystals, van der Waals forces, and applications of methods of quantum field theory". In particular he is known for the Dzyaloshinskii-Moriya interaction. Biography He was born in Moscow to a Jewish family. His father, Yechiel Moiseevich Dzyaloshinskii (1897–1942), a native of Kalush, Ukraine, died in captivity in early 1942. The first in his family to attend a university, Igor E. Dzyaloshinskii graduated in 1953 from the faculty of physics of Moscow State University. Dzyaloshinski pursued graduate study at the Institute of Physics of the Russian Academy of Sciences, where he received in 1957 his Russian Candidate of Sciences degree (Ph. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feynman Diagram
In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced the diagrams in 1948. The calculation of probability amplitudes in theoretical particle physics requires the use of large, complicated integrals over a large number of variables. Feynman diagrams instead represent these integrals graphically. Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. According to David Kaiser, "Since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations. Feynman diagrams have revolutionized nearly every aspect of theoretical physics." While the diagrams apply primarily to quantum field theory, they can be used in other areas of physics, such as solid-state theory. Frank Wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matsubara Frequency 1
is a city located in Osaka Prefecture, Japan. , the city had an estimated population of 117,811 in 57351 households and a population density of 7100 persons per km2. The total area of the city is . Geography Matsubara is located in the center of Osaka Prefecture. The city measures approximately 5.8 kilometers east–west by 5.1 kilometers north–south, and is mostly flatland. Neighboring municipalities Osaka Prefecture *Fujiidera *Habikino *Osaka ( Sumiyoshi-ku, Higashi Sumiyoshi-ku, Hirano-ku) *Sakai ( Kita-ku, Mihara-ku) * Yao Climate Matsubara has a Humid subtropical climate (Köppen ''Cfa'') characterized by warm summers and cool winters with light to no snowfall. The average annual temperature in Matsubara is 14.9 °C. The average annual rainfall is 1475 mm with September as the wettest month. The temperatures are highest on average in August, at around 27.0 °C, and lowest in January, at around 3.5 °C. Demographics Per Japanese census data, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pole (complex Analysis)
In complex analysis (a branch of mathematics), a pole is a certain type of singularity (mathematics), singularity of a complex-valued function of a complex number, complex variable. It is the simplest type of non-removable singularity of such a function (see essential singularity). Technically, a point is a pole of a function if it is a zero of a function, zero of the function and is holomorphic function, holomorphic (i.e. complex differentiable) in some neighbourhood (mathematics), neighbourhood of . A function is meromorphic function, meromorphic in an open set if for every point of there is a neighborhood of in which at least one of and is holomorphic. If is meromorphic in , then a zero of is a pole of , and a pole of is a zero of . This induces a duality between ''zeros'' and ''poles'', that is fundamental for the study of meromorphic functions. For example, if a function is meromorphic on the whole complex plane plus the point at infinity, then the sum of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Residue (complex Analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities. (More generally, residues can be calculated for any function f\colon \mathbb \setminus \_k \rightarrow \mathbb that is holomorphic except at the discrete points ''k'', even if some of them are essential singularities.) Residues can be computed quite easily and, once known, allow the determination of general contour integrals via the residue theorem. Definition The residue of a meromorphic function f at an isolated singularity a, often denoted \operatorname(f,a), \operatorname_a(f), \mathop_f(z) or \mathop_f(z), is the unique value R such that f(z)- R/(z-a) has an analytic antiderivative in a punctured disk 0<\vert z-a\vert<\delta. Alternatively, residues can be calculated by finding |
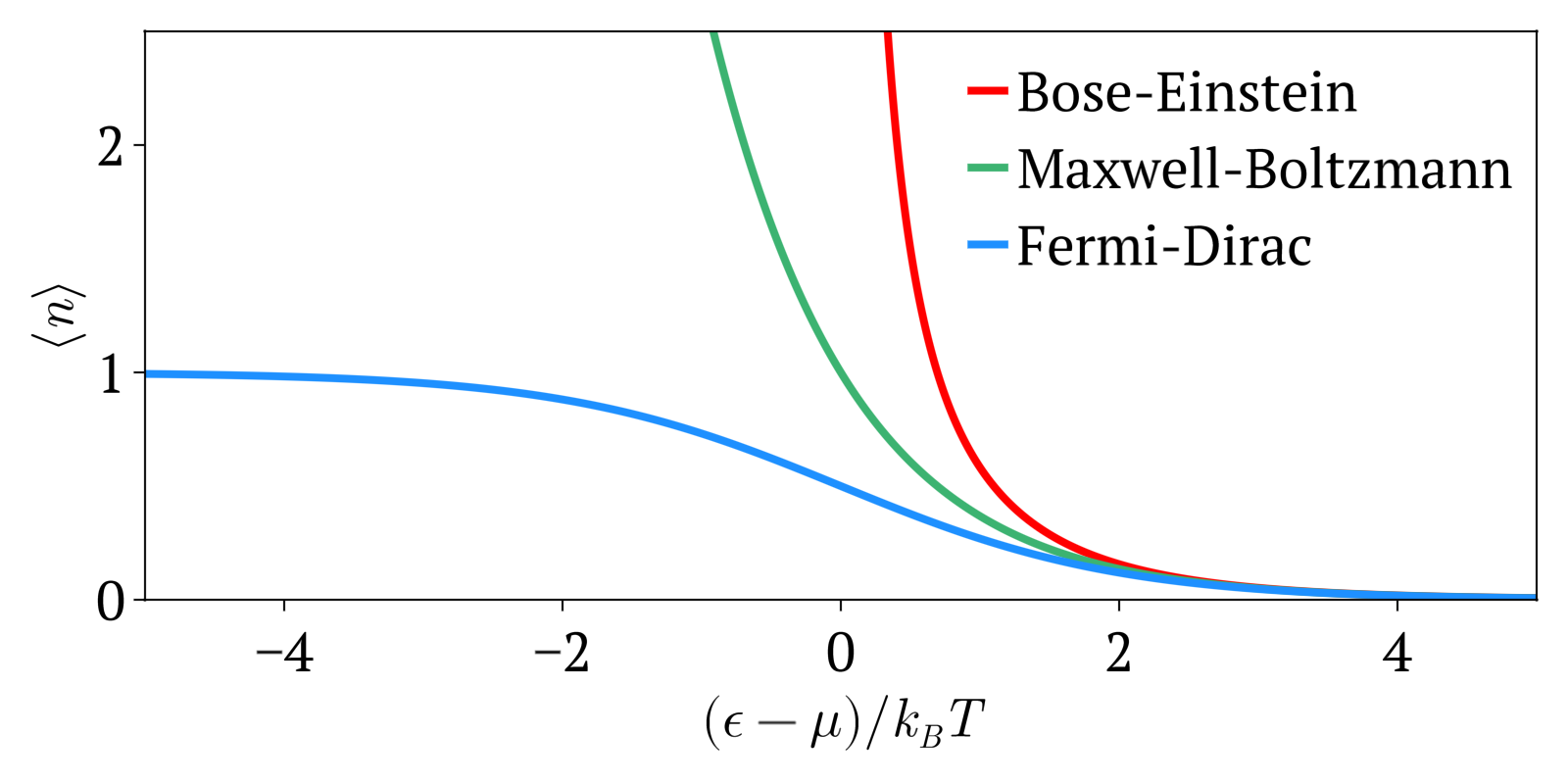
Bose–Einstein Statistics
In quantum statistics, Bose–Einstein statistics (B–E statistics) describes one of two possible ways in which a collection of non-interacting identical particles may occupy a set of available discrete energy states at thermodynamic equilibrium. The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics, accounts for the cohesive streaming of laser light and the frictionless creeping of superfluid helium. The theory of this behaviour was developed (1924–25) by Satyendra Nath Bose, who recognized that a collection of identical and indistinguishable particles could be distributed in this way. The idea was later adopted and extended by Albert Einstein in collaboration with Bose. Bose–Einstein statistics apply only to particles that do not follow the Pauli exclusion principle restrictions. Particles that follow Bose-Einstein statistics are called bosons, which have integer values of spin. In contrast, particles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |