|
Matrix-free Methods
In computational mathematics, a matrix-free method is an algorithm for solving a linear system of equations or an eigenvalue problem that does not store the coefficient matrix explicitly, but accesses the matrix by evaluating matrix-vector products. Such methods can be preferable when the matrix is so big that storing and manipulating it would cost a lot of memory and computing time, even with the use of methods for sparse matrices. Many iterative methods allow for a matrix-free implementation, including: * the power method, * the Lanczos algorithm, * Locally Optimal Block Preconditioned Conjugate Gradient Method ( LOBPCG), * Wiedemann's coordinate recurrence algorithm, * the conjugate gradient method, * Krylov subspace methods. Distributed solutions have also been explored using coarse-grain parallel software systems to achieve homogeneous solutions of linear systems. It is generally used in solving non-linear equations like Euler's equations in computational fluid dynamics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Mathematics
Computational mathematics is the study of the interaction between mathematics and calculations done by a computer.National Science Foundation, Division of Mathematical ScienceProgram description PD 06-888 Computational Mathematics 2006. Retrieved April 2007. A large part of computational mathematics consists roughly of using mathematics for allowing and improving computer computation in areas of science and engineering where mathematics are useful. This involves in particular algorithm design, computational complexity, numerical methods and computer algebra. Computational mathematics refers also to the use of computers for mathematics itself. This includes mathematical experimentation for establishing conjectures (particularly in number theory), the use of computers for proving theorems (for example the four color theorem), and the design and use of proof assistants. Areas of computational mathematics Computational mathematics emerged as a distinct part of applied mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear System Of Equations
In mathematics, a system of linear equations (or linear system) is a collection of two or more linear equations involving the same variables. For example, : \begin 3x+2y-z=1\\ 2x-2y+4z=-2\\ -x+\fracy-z=0 \end is a system of three equations in the three variables . A '' solution'' to a linear system is an assignment of values to the variables such that all the equations are simultaneously satisfied. In the example above, a solution is given by the ordered triple (x,y,z)=(1,-2,-2), since it makes all three equations valid. Linear systems are a fundamental part of linear algebra, a subject used in most modern mathematics. Computational algorithms for finding the solutions are an important part of numerical linear algebra, and play a prominent role in engineering, physics, chemistry, computer science, and economics. A system of non-linear equations can often be approximated by a linear system (see linearization), a helpful technique when making a mathematical model or computer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Princeton University Press
Princeton University Press is an independent publisher with close connections to Princeton University. Its mission is to disseminate scholarship within academia and society at large. The press was founded by Whitney Darrow, with the financial support of Charles Scribner, as a printing press to serve the Princeton community in 1905. Its distinctive building was constructed in 1911 on William Street in Princeton. Its first book was a new 1912 edition of John Witherspoon's ''Lectures on Moral Philosophy.'' History Princeton University Press was founded in 1905 by a recent Princeton graduate, Whitney Darrow, with financial support from another Princetonian, Charles Scribner II. Darrow and Scribner purchased the equipment and assumed the operations of two already existing local publishers, that of the ''Princeton Alumni Weekly'' and the Princeton Press. The new press printed both local newspapers, university documents, '' The Daily Princetonian'', and later added book publishing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements (e.g., ''m'' × ''n'' for an ''m'' × ''n'' matrix) is sometimes referred to as the sparsity of the matrix. Conceptually, sparsity corresponds to systems with few pairwise interactions. For example, consider a line of balls connected by springs from one to the next: this is a sparse system, as only adjacent balls are coupled. By contrast, if the same line of balls were to have springs connecting each ball to all other balls, the system would correspond to a dense matrix. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative Method
In computational mathematics, an iterative method is a Algorithm, mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the ''i''-th approximation (called an "iterate") is derived from the previous ones. A specific implementation with Algorithm#Termination, termination criteria for a given iterative method like gradient descent, hill climbing, Newton's method, or Quasi-Newton method, quasi-Newton methods like Broyden–Fletcher–Goldfarb–Shanno algorithm, BFGS, is an algorithm of an iterative method or a method of successive approximation. An iterative method is called ''Convergent series, convergent'' if the corresponding sequence converges for given initial approximations. A mathematically rigorous convergence analysis of an iterative method is usually performed; however, heuristic-based iterative methods are also common. In contrast, direct methods attempt to solve the problem by a finit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
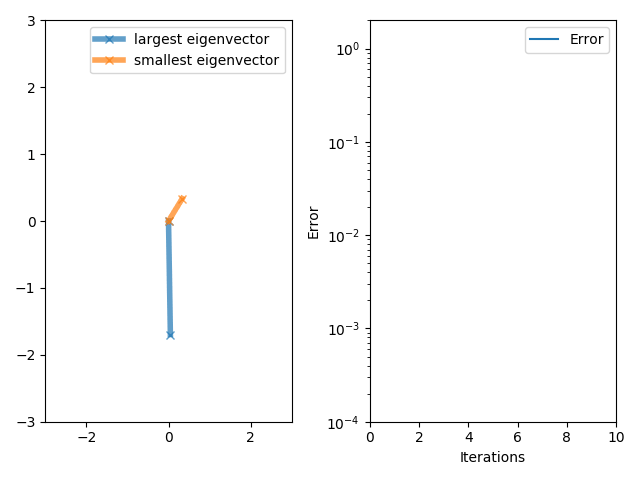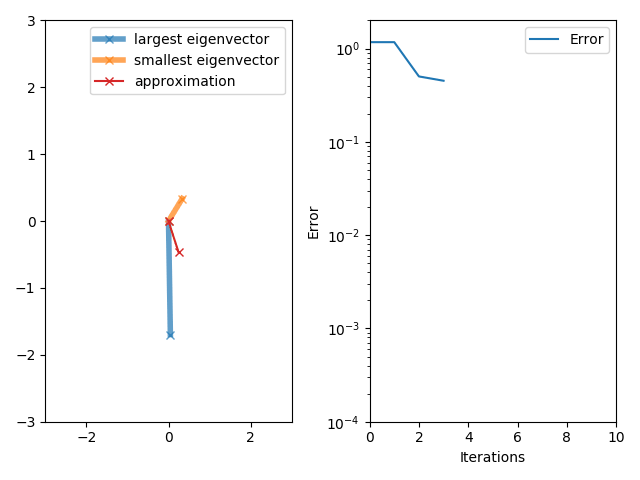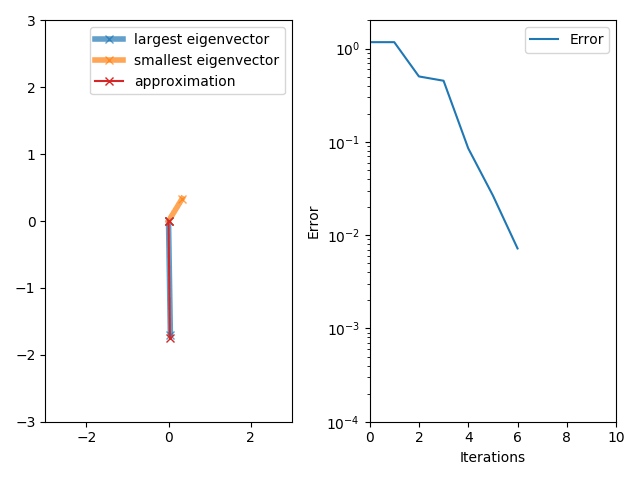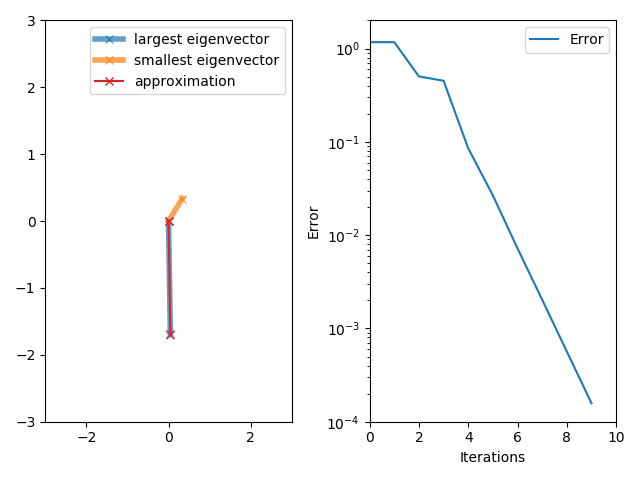
Power Method
In mathematics, power iteration (also known as the power method) is an eigenvalue algorithm: given a diagonalizable matrix A, the algorithm will produce a number \lambda, which is the greatest (in absolute value) eigenvalue of A, and a nonzero vector v, which is a corresponding eigenvector of \lambda, that is, Av = \lambda v. The algorithm is also known as the Von Mises iteration. Richard von Mises and H. Pollaczek-Geiringer, ''Praktische Verfahren der Gleichungsauflösung'', ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 9, 152-164 (1929). Power iteration is a very simple algorithm, but it may converge slowly. The most time-consuming operation of the algorithm is the multiplication of matrix A by a vector, so it is effective for a very large sparse matrix with appropriate implementation. The speed of convergence is like (\lambda_2 / \lambda_1)^k where k is the number of iterations (see a later section). In words, convergence is exponential with base being the spect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lanczos Algorithm
The Lanczos algorithm is an iterative method devised by Cornelius Lanczos that is an adaptation of power iteration, power methods to find the m "most useful" (tending towards extreme highest/lowest) eigenvalues and eigenvectors of an n \times n Hermitian matrix, where m is often but not necessarily much smaller than n . Although computationally efficient in principle, the method as initially formulated was not useful, due to its Numerical stability, numerical instability. In 1970, Ojalvo and Newman showed how to make the method numerically stable and applied it to the solution of very large engineering structures subjected to dynamic loading. This was achieved using a method for purifying the Lanczos vectors (i.e. by repeatedly reorthogonalizing each newly generated vector with all previously generated ones) to any degree of accuracy, which when not performed, produced a series of vectors that were highly contaminated by those associated with the lowest natural frequencies. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LOBPCG
Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) is a matrix-free method for finding the largest (or smallest) eigenvalues and the corresponding eigenvectors of a symmetric generalized eigenvalue problem :A x= \lambda B x, for a given pair (A, B) of complex Hermitian or real symmetric matrices, where the matrix B is also assumed positive-definite. Background Kantorovich in 1948 proposed calculating the smallest eigenvalue \lambda_1 of a symmetric matrix A by steepest descent using a direction r = Ax-\lambda (x) x of a scaled gradient of a Rayleigh quotient \lambda(x) = (x, Ax)/(x, x) in a scalar product (x, y) = x'y, with the step size computed by minimizing the Rayleigh quotient in the linear span of the vectors x and r, i.e. in a locally optimal manner. Samokish proposed applying a preconditioner T to the residual vector r to generate the preconditioned direction w = T r and derived asymptotic, as x approaches the eigenvector, convergence rate bounds. D'yakonov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SIAM Journal On Scientific Computing
The ''SIAM Journal on Scientific Computing'' (''SISC''), formerly ''SIAM Journal on Scientific & Statistical Computing'', is a scientific journal focusing on the research articles on numerical methods and techniques for scientific computation. It is published by the Society for Industrial and Applied Mathematics (SIAM). Hans De Sterck is the current editor-in-chief, assuming the role in January 2022. The impact factor is currently around 2. This journal papers address computational issues relevant to solution of scientific or engineering problems and include computational results demonstrating the effectiveness of proposed techniques. They are classified into three categories: 1) Methods and Algorithms for Scientific Computing. 2) Computational Methods in Science and Engineering. 3) Software and High-Performance Computing. The first type papers focus on theoretical analysis, provided that relevance to applications in science and engineering is demonstrated. They are supposed to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Gradient Method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-semidefinite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |