|
Mathematical Programming With Equilibrium Constraints
Mathematical programming with equilibrium constraints (MPEC) is the study of constrained optimization problems where the constraints include variational inequalities or complementarities. MPEC is related to the Stackelberg game. MPEC is used in the study of engineering design, economic equilibrium, and multilevel games. MPEC is difficult to deal with because its feasible region is not necessarily convex or even connected Connected may refer to: Film and television * ''Connected'' (2008 film), a Hong Kong remake of the American movie ''Cellular'' * '' Connected: An Autoblogography About Love, Death & Technology'', a 2011 documentary film * ''Connected'' (2015 TV .... References * Z.-Q. Luo, J.-S. Pang and D. Ralph: ''Mathematical Programs with Equilibrium Constraints''. Cambridge University Press, 1996, . * B. Baumrucker, J. Renfro, L. T. Biegler, MPEC problem formulations and solution strategies with chemical engineering applications, Computers & Chemical Engineering, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constrained Optimization
In mathematical optimization, constrained optimization (in some contexts called constraint optimization) is the process of optimizing an objective function with respect to some variables in the presence of constraints on those variables. The objective function is either a cost function or energy function, which is to be minimized, or a reward function or utility function, which is to be maximized. Constraints can be either hard constraints, which set conditions for the variables that are required to be satisfied, or soft constraints, which have some variable values that are penalized in the objective function if, and based on the extent that, the conditions on the variables are not satisfied. Relation to constraint-satisfaction problems The constrained-optimization problem (COP) is a significant generalization of the classic constraint-satisfaction problem (CSP) model. COP is a CSP that includes an ''objective function'' to be optimized. Many algorithms are used to handle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Inequalities
In mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all possible values of a given variable, belonging usually to a convex set. The mathematical theory of variational inequalities was initially developed to deal with equilibrium problems, precisely the Signorini problem: in that model problem, the functional involved was obtained as the first variation of the involved potential energy. Therefore, it has a variational origin, recalled by the name of the general abstract problem. The applicability of the theory has since been expanded to include problems from economics, finance, optimization and game theory. History The first problem involving a variational inequality was the Signorini problem, posed by Antonio Signorini in 1959 and solved by Gaetano Fichera in 1963, according to the references and : the first papers of the theory were and , . Later on, Guido Stampacchia proved his generalization to the Lax–Milgram the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complementarity Theory
A complementarity problem is a type of mathematical optimization problem. It is the problem of optimizing (minimizing or maximizing) a function of two vector variables subject to certain requirements (constraints) which include: that the inner product of the two vectors must equal zero, i.e. they are orthogonal. In particular for finite-dimensional real vector spaces this means that, if one has vectors ''X'' and ''Y'' with all ''nonnegative'' components (''x''''i'' ≥ 0 and ''y''''i'' ≥ 0 for all i: in the first quadrant if 2-dimensional, in the first octant if 3-dimensional), then for each pair of components ''x''''i'' and ''y''''i'' one of the pair must be zero, hence the name ''complementarity''. e.g. ''X'' = (1, 0) and ''Y'' = (0, 2) are complementary, but ''X'' = (1, 1) and ''Y'' = (2, 0) are not. A complementarity problem is a special case of a variational inequality. History Complementarity p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Engineering Design
The engineering design process is a common series of steps that engineers use in creating functional products and processes. The process is highly iterative - parts of the process often need to be repeated many times before another can be entered - though the part(s) that get iterated and the number of such cycles in any given project may vary. It is a decision making process (often iterative) in which the basic sciences, mathematics, and engineering sciences are applied to convert resources optimally to meet a stated objective. Among the fundamental elements of the design process are the establishment of objectives and criteria, synthesis, analysis, construction, testing and evaluation. Common stages of the engineering design process It's important to understand that there are various framings/articulations of the engineering design process. Different terminology employed may have varying degrees of overlap, which affects what steps get stated explicitly or deemed "high lev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
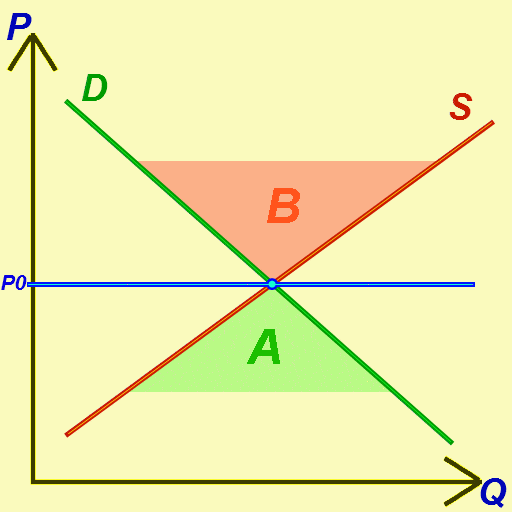
Economic Equilibrium
In economics, economic equilibrium is a situation in which economic forces such as supply and demand are balanced and in the absence of external influences the ( equilibrium) values of economic variables will not change. For example, in the standard text perfect competition, equilibrium occurs at the point at which quantity demanded and quantity supplied are equal. Market equilibrium in this case is a condition where a market price is established through competition such that the amount of goods or services sought by buyers is equal to the amount of goods or services produced by sellers. This price is often called the competitive price or market clearing price and will tend not to change unless demand or supply changes, and quantity is called the "competitive quantity" or market clearing quantity. But the concept of ''equilibrium'' in economics also applies to imperfectly competitive markets, where it takes the form of a Nash equilibrium. Understanding economic equilibriu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multilevel Games
Multilevel or multi-level may refer to: * A hierarchy A hierarchy (from Greek: , from , 'president of sacred rites') is an arrangement of items (objects, names, values, categories, etc.) that are represented as being "above", "below", or "at the same level as" one another. Hierarchy is an important ..., a system where items are arranged in an "above-below" relation. * A system that is composed of several layers. * Bombardier MultiLevel Coach, a passenger rail car by Bombardier. See also * * {{dab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feasible Region
In mathematical optimization, a feasible region, feasible set, search space, or solution space is the set of all possible points (sets of values of the choice variables) of an optimization problem that satisfy the problem's constraints, potentially including inequalities, equalities, and integer constraints. This is the initial set of candidate solutions to the problem, before the set of candidates has been narrowed down. For example, consider the problem of minimizing the function x^2+y^4 with respect to the variables x and y, subject to 1 \le x \le 10 and 5 \le y \le 12. \, Here the feasible set is the set of pairs (''x'', ''y'') in which the value of ''x'' is at least 1 and at most 10 and the value of ''y'' is at least 5 and at most 12. The feasible set of the problem is separate from the objective function, which states the criterion to be optimized and which in the above example is x^2+y^4. In many problems, the feasible set reflects a constraint that one or more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment (possibly empty). For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary of a convex set is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connected Space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that are used to distinguish topological spaces. A subset of a topological space X is a if it is a connected space when viewed as a subspace of X. Some related but stronger conditions are path connected, simply connected, and n-connected. Another related notion is ''locally connected'', which neither implies nor follows from connectedness. Formal definition A topological space X is said to be if it is the union of two disjoint non-empty open sets. Otherwise, X is said to be connected. A subset of a topological space is said to be connected if it is connected under its subspace topology. Some authors exclude the empty set (with its unique topology) as a connected space, but this article does not follow that practice. For a topologi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
