|
Mathematical Optimisation
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Optimization problems can be divided into two categories, depending on whether the variables ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Paraboloid
Max or MAX may refer to: Animals * Max (American dog) (1983–2013), at one time purported to be the world's oldest living dog * Max (British dog), the first pet dog to win the PDSA Order of Merit (animal equivalent of the OBE) * Max (gorilla) (1971–2004), a western lowland gorilla at the Johannesburg Zoo who was shot by a criminal in 1997 Brands and enterprises * Australian Max Beer * Max Hamburgers, a fast-food corporation * MAX Index, a Hungarian domestic government bond index * Max Fashion, an Indian clothing brand Computing * MAX (operating system), a Spanish-language Linux version * Max (software), a music programming language * MAX Machine * Multimedia Acceleration eXtensions, extensions for HP PA-RISC Films * Max (1994 film), ''Max'' (1994 film), a Canadian film by Charles Wilkinson * Max (2002 film), ''Max'' (2002 film), a film about Adolf Hitler * Max (2015 film), ''Max'' (2015 film), an American war drama film * Max (2024 film), ''Max'' (2024 film), an Indian Kannad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
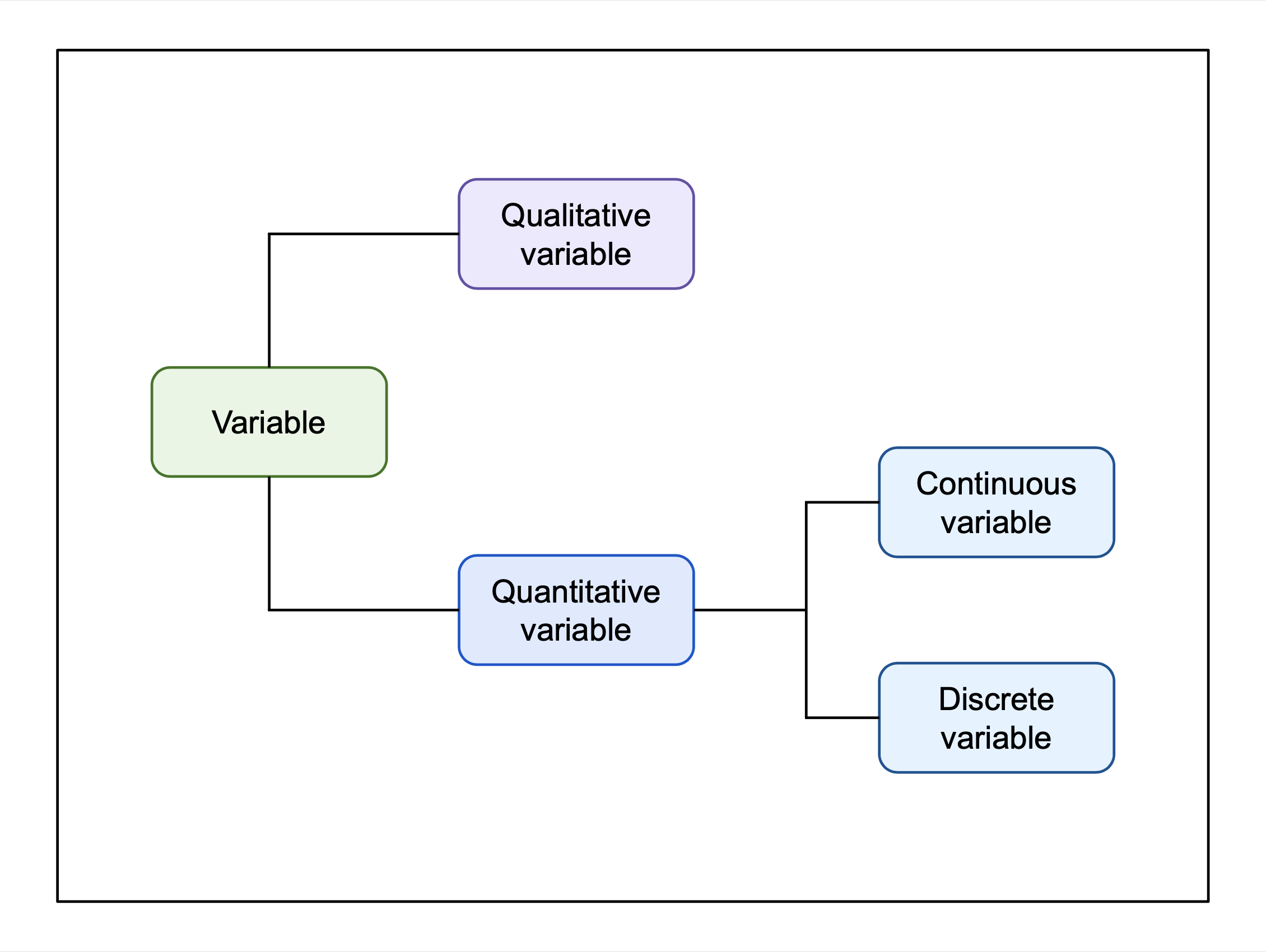
Discrete Variable
In mathematics and statistics, a quantitative variable may be continuous or discrete. If it can take on two real values and all the values between them, the variable is continuous in that interval. If it can take on a value such that there is a non-infinitesimal gap on each side of it containing no values that the variable can take on, then it is discrete around that value. In some contexts, a variable can be discrete in some ranges of the number line and continuous in others. In statistics, continuous and discrete variables are distinct statistical data types which are described with different probability distributions. Continuous variable A continuous variable is a variable such that there are possible values between any two values. For example, a variable over a non-empty range of the real numbers is continuous if it can take on any value in that range. Methods of calculus are often used in problems in which the variables are continuous, for example in continuous optimi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History
History is the systematic study of the past, focusing primarily on the Human history, human past. As an academic discipline, it analyses and interprets evidence to construct narratives about what happened and explain why it happened. Some theorists categorize history as a social science, while others see it as part of the humanities or consider it a hybrid discipline. Similar debates surround the purpose of history—for example, whether its main aim is theoretical, to uncover the truth, or practical, to learn lessons from the past. In a more general sense, the term ''history'' refers not to an academic field but to the past itself, times in the past, or to individual texts about the past. Historical research relies on Primary source, primary and secondary sources to reconstruct past events and validate interpretations. Source criticism is used to evaluate these sources, assessing their authenticity, content, and reliability. Historians strive to integrate the perspectives o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear function#As a polynomial function, linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the mathematical optimization, optimization of a linear objective function, subject to linear equality and linear inequality Constraint (mathematics), constraints. Its feasible region is a convex polytope, which is a set defined as the intersection (mathematics), intersection of finitely many Half-space (geometry), half spaces, each of which is defined by a linear inequality. Its objective function is a real number, real-valued affine function, affine (linear) function defined on this polytope. A linear programming algorithm finds a point in the po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Programming
Computer programming or coding is the composition of sequences of instructions, called computer program, programs, that computers can follow to perform tasks. It involves designing and implementing algorithms, step-by-step specifications of procedures, by writing source code, code in one or more programming languages. Programmers typically use high-level programming languages that are more easily intelligible to humans than machine code, which is directly executed by the central processing unit. Proficient programming usually requires expertise in several different subjects, including knowledge of the Domain (software engineering), application domain, details of programming languages and generic code library (computing), libraries, specialized algorithms, and Logic#Formal logic, formal logic. Auxiliary tasks accompanying and related to programming include Requirements analysis, analyzing requirements, Software testing, testing, debugging (investigating and fixing problems), imple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
In mathematics, a set is a collection of different things; the things are '' elements'' or ''members'' of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. Context Before the end of the 19th century, sets were not studied specifically, and were not clearly distinguished from sequences. Most mathematicians considered infinity as potentialmeaning that it is the result of an endless processand were reluctant to consider infinite sets, that is sets whose number of members is not a natural number. Specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constrained Optimization
In mathematical optimization, constrained optimization (in some contexts called constraint optimization) is the process of optimizing an objective function with respect to some variables in the presence of constraints on those variables. The objective function is either a cost function or energy function, which is to be minimized, or a reward function or utility function, which is to be maximized. Constraints can be either hard constraints, which set conditions for the variables that are required to be satisfied, or soft constraints, which have some variable values that are penalized in the objective function if, and based on the extent that, the conditions on the variables are not satisfied. Relation to constraint-satisfaction problems The constrained-optimization problem (COP) is a significant generalization of the classic constraint-satisfaction problem (CSP) model. COP is a CSP that includes an ''objective function'' to be optimized. Many algorithms are used to hand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countable Set
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (the number of elements of the set) is not greater than that of the natural numbers. A countable set that is not finite is said to be countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph (discrete Mathematics)
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a Set (mathematics), set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', then this graph is directed, because owing mon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |