|
Lyapunov Function
In the theory of ordinary differential equations (ODEs), Lyapunov functions, named after Aleksandr Lyapunov, are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Lyapunov functions (also called Lyapunov’s second method for stability) are important to stability theory of dynamical systems and control theory. A similar concept appears in the theory of general state space Markov chains, usually under the name Foster–Lyapunov functions. For certain classes of ODEs, the existence of Lyapunov functions is a necessary and sufficient condition for stability. Whereas there is no general technique for constructing Lyapunov functions for ODEs, in many specific cases the construction of Lyapunov functions is known. For instance, quadratic functions suffice for systems with one state; the solution of a particular linear matrix inequality provides Lyapunov functions for linear systems; and conservation laws can often be used to construct Lyapunov funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equations
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathematics are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Function
In mathematics, a positive-definite function is, depending on the context, either of two types of function. Most common usage A ''positive-definite function'' of a real variable ''x'' is a complex-valued function f: \mathbb \to \mathbb such that for any real numbers ''x''1, …, ''x''''n'' the ''n'' × ''n'' matrix : A = \left(a_\right)_^n~, \quad a_ = f(x_i - x_j) is positive ''semi-''definite (which requires ''A'' to be Hermitian; therefore ''f''(−''x'') is the complex conjugate of ''f''(''x'')). In particular, it is necessary (but not sufficient) that : f(0) \geq 0~, \quad , f(x), \leq f(0) (these inequalities follow from the condition for ''n'' = 1, 2.) A function is ''negative semi-definite'' if the inequality is reversed. A function is ''definite'' if the weak inequality is replaced with a strong ( 0). Examples If (X, \langle \cdot, \cdot \rangle) is a real inner product space, then g_y \colon X \to \mathbb, x \mapsto \exp(i \langle y, x \rangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Foster's Theorem
In probability theory, Foster's theorem, named after Gordon Foster, is used to draw conclusions about the positive recurrence of Markov chains with countable state spaces. It uses the fact that positive recurrent Markov chains exhibit a notion of "Lyapunov stability" in terms of returning to any state while starting from it within a finite time interval. Theorem Consider an irreducible discrete-time Markov chain on a countable state space ''S'' having a transition probability matrix P with elements ''p''''ij'' for pairs ''i'', ''j'' in ''S''. Foster's theorem states that the Markov chain is positive recurrent if and only if there exists a Lyapunov function V: S \to \mathbb, such that V(i) \geq 0 \text \forall \text i \in S and # \sum_p_V(j) < for # for all for some finite set ''F'' and strictly positive ''ε''. Related links * |
Chetaev Function
The Chetaev instability theorem for dynamical systems states that if there exists, for the system \dot = X(\textbf) with an equilibrium point at the origin, a continuously differentiable function V(x) such that # the origin is a boundary point of the set G = \; # there exists a neighborhood U of the origin such that \dot(\textbf)>0 for all \mathbf \in G \cap U then the origin is an unstable equilibrium point of the system. This theorem is somewhat less restrictive than the Lyapunov instability theorems, since a complete sphere (circle) around the origin for which V and \dot both are of the same sign does not have to be produced. It is named after Nicolai Gurevich Chetaev. Applications Chetaev instability theorem has been used to analyze the unfolding dynamics of proteins under the effect of optical tweezers. See also * Lyapunov function — a function whose existence guarantees stability References * Further reading *{{cite journal , doi=10.4249/scholarpedia.4672, doi-access ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control-Lyapunov Function
In control theory, a control-Lyapunov function (CLF) is an extension of the idea of Lyapunov function V(x) to systems with control inputs. The ordinary Lyapunov function is used to test whether a dynamical system is ''(Lyapunov) stable'' or (more restrictively) ''asymptotically stable''. Lyapunov stability means that if the system starts in a state x \ne 0 in some domain ''D'', then the state will remain in ''D'' for all time. For ''asymptotic stability'', the state is also required to converge to x = 0. A control-Lyapunov function is used to test whether a system is ''asymptotically stabilizable'', that is whether for any state ''x'' there exists a control u(x,t) such that the system can be brought to the zero state asymptotically by applying the control ''u''. The theory and application of control-Lyapunov functions were developed by Zvi Artstein and Eduardo D. Sontag in the 1980s and 1990s. Definition Consider an autonomous dynamical system with inputs where x\in\mathbb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathematics are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
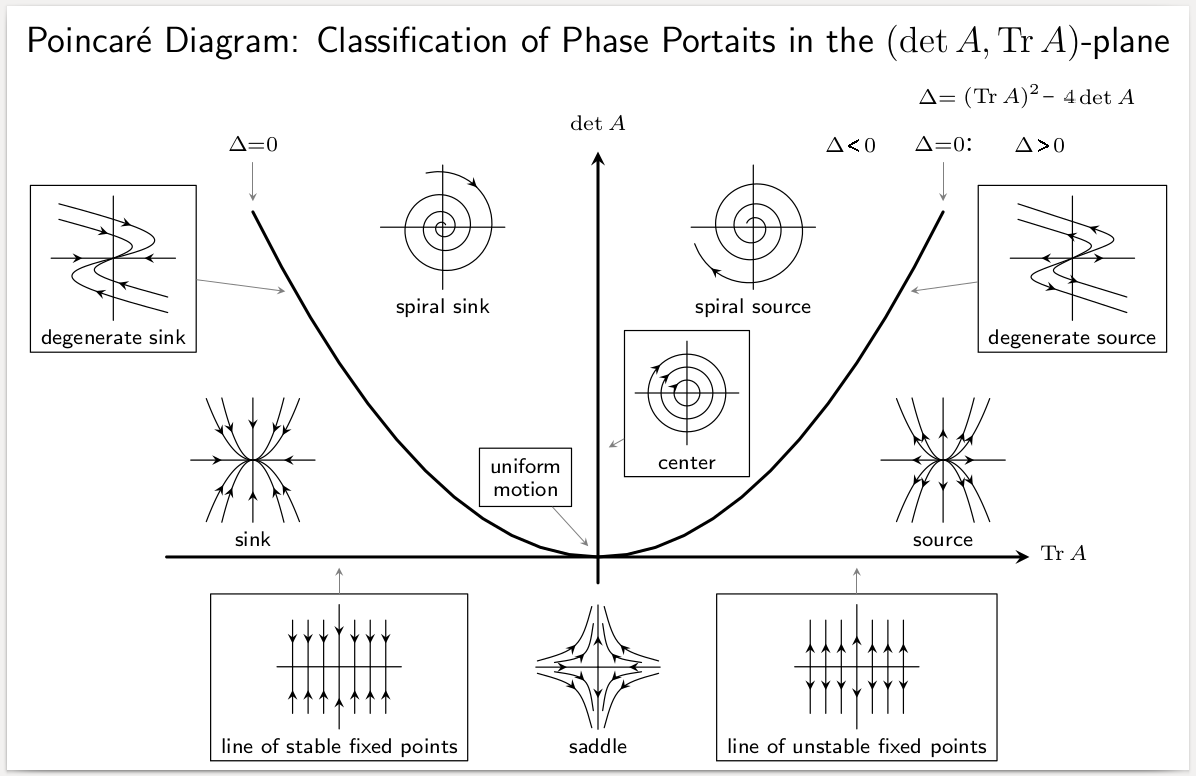
Lyapunov Stability
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Aleksandr Lyapunov. In simple terms, if the solutions that start out near an equilibrium point x_e stay near x_e forever, then x_e is Lyapunov stable. More strongly, if x_e is Lyapunov stable and all solutions that start out near x_e converge to x_e, then x_e is asymptotically stable. The notion of exponential stability guarantees a minimal rate of decay, i.e., an estimate of how quickly the solutions converge. The idea of Lyapunov stability can be extended to infinite-dimensional manifolds, where it is known as structural stability, which concerns the behavior of different but "nearby" solutions to differential equations. Input-to-state stability (ISS) applies Lyapunov notions to systems with inputs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radially Unbounded Function
In mathematics, a radially unbounded function is a function f: \mathbb^n \rightarrow \mathbb for which :\, x\, \to \infty \Rightarrow f(x) \to \infty. Or equivalently, :\forall c > 0:\exists r > 0 : \forall x \in \mathbb^n: _r_\Rightarrow_f(x)_>_c.html" ;"title="Vert x \Vert > r \Rightarrow f(x) > c">Vert x \Vert > r \Rightarrow f(x) > c/math> Such functions are applied in control theory and required in optimization for determination of compact space In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no "punctures" or "missing endpoints", i ...s. Notice that the norm used in the definition can be any norm defined on \mathbb^n , and that the behavior of the function along the axes does not necessarily reveal that it is radially unbounded or not; i.e. to be radially unbounded the condition must be verified along any pat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
José Luis Massera
José Luis Massera (Genoa, Italy, June 8, 1915 – Montevideo, September 9, 2002) was a Uruguayan dissident and mathematician who researched the stability of differential equations. Massera's lemma is named after him. He published over 40 papers during 1940–1970. A militant Communist, he was a political prisoner during 1975–1984. In the 1930s, Julio Rey Pastor gave regular weekend lectures on topology in Montevideo to a group that included Massera. Stimulated by contact with Argentine mathematics, the 1950s saw Uruguay develop a fine school in mathematics, of which Massera was very much a part. Massera developed new notions of stability, and published several foundational papers and an influential textbook. His results in on periodic differential equations have been heavily cited and are referred to as Massera's theorem. His work in and on the converse to Lyapunov's criterion is also influential, and contain the well known Massera's lemma. His textbook is also he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stability Theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later time as a result of the maximum principle. In partial differential equations one may measure the distances between functions using Lp norms or the sup norm, while in differential geometry one may measure the distance between spaces using the Gromov–Hausdorff distance. In dynamical systems, an orbit is called ''Lyapunov stable'' if the forward orbit of any point is in a small enough neighborhood or it stays in a small (but perhaps, larger) neighborhood. Various criteria have been developed to prove stability or instability of an orbit. Under favorable circumstances, the question may be reduced to a well-studied problem involvi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Function
In mathematics and physics, a scalar field is a function associating a single number to every point in a space – possibly physical space. The scalar may either be a pure mathematical number (dimensionless) or a scalar physical quantity (with units). In a physical context, scalar fields are required to be independent of the choice of reference frame, meaning that any two observers using the same units will agree on the value of the scalar field at the same absolute point in space (or spacetime) regardless of their respective points of origin. Examples used in physics include the temperature distribution throughout space, the pressure distribution in a fluid, and spin-zero quantum fields, such as the Higgs field. These fields are the subject of scalar field theory. Definition Mathematically, a scalar field on a region ''U'' is a real or complex-valued function or distribution on ''U''. The region ''U'' may be a set in some Euclidean space, Minkowski space, or more generall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aleksandr Lyapunov
Aleksandr Mikhailovich Lyapunov (russian: Алекса́ндр Миха́йлович Ляпуно́в, ; – 3 November 1918) was a Russian mathematician, mechanician and physicist. His surname is variously romanized as Ljapunov, Liapunov, Liapounoff or Ljapunow. He was the son of the astronomer Mikhail Lyapunov and the brother of the pianist and composer Sergei Lyapunov. Lyapunov is known for his development of the stability theory of a dynamical system, as well as for his many contributions to mathematical physics and probability theory. Biography Early life Lyapunov was born in Yaroslavl, Russian Empire. His father Mikhail Vasilyevich Lyapunov (1820–1868) was an astronomer employed by the Demidov Lyceum. His brother, Sergei Lyapunov, was a gifted composer and pianist. In 1863, M. V. Lyapunov retired from his scientific career and relocated his family to his wife's estate at Bolobonov, in the Simbirsk province (now Ulyanovsk Oblast). After the death of his father in 18 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |