|
Loubignac Iteration
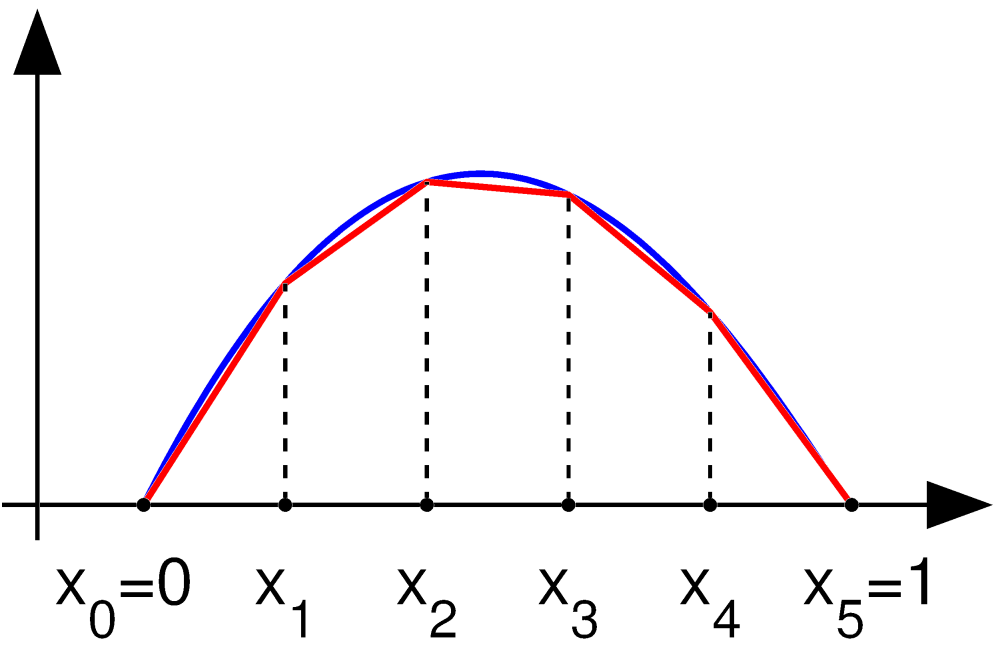
In applied mathematics, Loubignac iteration is an iterative method in finite element methods. It gives continuous stress field A stress field is the distribution of internal forces in a body that balance a given set of external forces. Stress fields are widely used in fluid dynamics and materials science. Consider that one can picture the stress fields as the stress cre .... It is named after Gilles Loubignac, who published the method in 1977. References Loubignac's paper Continuum mechanics Finite element method Numerical differential equations Partial differential equations Structural analysis {{applied-math-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative Method
In computational mathematics, an iterative method is a Algorithm, mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the ''n''-th approximation is derived from the previous ones. A specific implementation of an iterative method, including the Algorithm#Termination, termination criteria, is an algorithm of the iterative method. An iterative method is called convergent if the corresponding sequence converges for given initial approximations. A mathematically rigorous convergence analysis of an iterative method is usually performed; however, heuristic-based iterative methods are also common. In contrast, direct methods attempt to solve the problem by a finite sequence of operations. In the absence of rounding errors, direct methods would deliver an exact solution (for example, solving a linear system of equations A\mathbf=\mathbf by Gaussian elimination). Iterative methods are often the only cho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Element Method
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The FEM is a general numerical method for solving partial differential equations in two or three space variables (i.e., some boundary value problems). To solve a problem, the FEM subdivides a large system into smaller, simpler parts that are called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approximates the unknown function over the domain. The sim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress Field
A stress field is the distribution of internal forces in a body that balance a given set of external forces. Stress fields are widely used in fluid dynamics and materials science. Consider that one can picture the stress fields as the stress created by adding an extra half plane of atoms to a crystal. The bonds are clearly stretched around the location of the dislocation and this stretching causes the stress field to form. Atomic bonds farther and farther away from the dislocation centre are less and less stretched which is why the stress field dissipates as the distance from the dislocation centre increases. Each dislocation within the material has a stress field associated with it. The creation of these stress fields is a result of the material trying to dissipate mechanical energy that is being exerted on the material. By convention, these dislocations are labelled as either positive or negative depending on whether the stress field of the dislocation is mostly compressive or t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century. Explanation A continuum model assumes that the substance of the object fills the space it occupies. Modeling objects in this way ignores the fact that matter is made of atoms, and so is not continuous; however, on length scales much greater than that of inter-atomic distances, such models are highly accurate. These models can be used to derive differential equations that describe the behavior of such objects using physical laws, such as mass conservation, momentum conservation, and energy conservation, and some information about the material is provided by constitutive relationships. Continuum mechanics deals with the physical properties of solids and fluids which are independent of any particular coordinate sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Element Method
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The FEM is a general numerical method for solving partial differential equations in two or three space variables (i.e., some boundary value problems). To solve a problem, the FEM subdivides a large system into smaller, simpler parts that are called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approximates the unknown function over the domain. The sim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Differential Equations
{{disambig ...
Numerical may refer to: * Number * Numerical digit * Numerical analysis Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |