|
List Of Surfaces
This is a list of surfaces, by Wikipedia page. ''See also List of algebraic surfaces, List of curves, Riemann surface.'' Minimal surfaces * Catalan's minimal surface * Costa's minimal surface * Catenoid * Enneper surface * Gyroid * Helicoid * Lidinoid * Riemann's minimal surface * Saddle tower * Scherk surface * Schwarz minimal surface * Triply periodic minimal surface Ruled surfaces * Catalan surface * Right conoid * Conical surface * helicoid * Developable rollers ( sphericon, oloid) * Hyperboloid of one sheet (doubly ruled) * Hyperbolic paraboloid (doubly ruled) * Rational normal scroll * Regulus Non-orientable surfaces *Klein bottle * Real projective plane ** Cross-cap ** Roman surface ** Boy's surface Quadrics *Sphere * Spheroid ** Oblate spheroid *Cone (geometry) *Ellipsoid * Hyperboloid of one sheet * Hyperboloid of two sheets * Hyperbolic paraboloid (a ruled surface) *Paraboloid Pseudospherical surfaces *Dini's surface * Pseudosphere Alge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface (mathematics)
In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line. There are several more precise definitions, depending on the context and the mathematical tools that are used for the study. The simplest mathematical surfaces are planes and spheres in the Euclidean 3-space. The exact definition of a surface may depend on the context. Typically, in algebraic geometry, a surface may cross itself (and may have other singularities), while, in topology and differential geometry, it may not. A surface is a topological space of dimension two; this means that a moving point on a surface may move in two directions (it has two degrees of freedom). In other words, around almost every point, there is a '' coordinate patch'' on which a two-dimensional coordinate system is defined. For example, the surface of the Earth resembles (i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ruled Surface
In geometry, a surface is ruled (also called a scroll) if through every point of there is a straight line that lies on . Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space. A ruled surface can be described as the set of points swept by a moving straight line. For example, a cone is formed by keeping one point of a line fixed whilst moving another point along a circle. A surface is ''doubly ruled'' if through every one of its points there are two distinct lines that lie on the surface. The hyperbolic paraboloid and the hyperboloid of one sheet are doubly ruled surfaces. The plane is the only surface which contains at least three distinct lines through each of its points . The properties of being ruled or doubly ruled are preserved by projective maps, and therefore are concepts of projective geometry. In algebrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Klein Bottle
In topology, a branch of mathematics, the Klein bottle () is an example of a non-orientable surface; it is a two-dimensional manifold against which a system for determining a normal vector cannot be consistently defined. Informally, it is a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. Other related non-orientable objects include the Möbius strip and the real projective plane. While a Möbius strip is a surface with boundary, a Klein bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary. The concept of a Klein bottle was first described in 1882 by the German mathematician Felix Klein. Construction The following square is a fundamental polygon of the Klein bottle. The idea is to 'glue' together the corresponding red and blue edges with the arrows matching, as in the diagrams below. Note that this is an "abstract" gluing in the sense that trying to rea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orientability
In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "counterclockwise". A space is orientable if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an orientation of the space. Real vector spaces, Euclidean spaces, and spheres are orientable. A space is non-orientable if "clockwise" is changed into "counterclockwise" after running through some loops in it, and coming back to the starting point. This means that a geometric shape, such as , that moves continuously along such a loop is changed into its own mirror image . A Möbius strip is an example of a non-orientable space. Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regulus (geometry)
In three-dimensional space, a regulus ''R'' is a set of skew lines, every point of which is on a transversal which intersects an element of ''R'' only once, and such that every point on a transversal lies on a line of ''R'' The set of transversals of ''R'' forms an opposite regulus ''S''. In ℝ3 the union ''R'' ∪ ''S'' is the ruled surface of a hyperboloid of one sheet. Three skew lines determine a regulus: :The locus of lines meeting three given skew lines is called a ''regulus''. Gallucci's theorem shows that the lines meeting the generators of the regulus (including the original three lines) form another "associated" regulus, such that every generator of either regulus meets every generator of the other. The two reguli are the two systems of generators of a ''ruled quadric''. According to Charlotte Scott, "The regulus supplies extremely simple proofs of the properties of a conic...the theorems of Chasles, Brianchon, and Pascal ..." In a finite geometry PG(3, ''q''), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Normal Scroll
In mathematics, a rational normal scroll is a ruled surface of degree ''n'' in projective space of dimension ''n'' + 1. Here "rational" means birational to projective space, "scroll" is an old term for ruled surface, and "normal" refers to projective normality (not normal schemes). A non-degenerate irreducible surface of degree ''m'' – 1 in P''m'' is either a rational normal scroll or the Veronese surface. Construction In projective space of dimension ''m'' + ''n'' + 1 choose two complementary linear subspaces of dimensions ''m'' > 0 and ''n'' > 0. Choose rational normal curves in these two linear subspaces, and choose an isomorphism φ between them. Then the rational normal surface consists of all lines joining the points ''x'' and ''φ''(''x''). In the degenerate case when one of ''m'' or ''n'' is 0, the rational normal scroll becomes a cone over a rational normal curve. If ''m'' < ''n'' then the rat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Paraboloid
In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry. Every plane section of a paraboloid by a plane parallel to the axis of symmetry is a parabola. The paraboloid is hyperbolic if every other plane section is either a hyperbola, or two crossing lines (in the case of a section by a tangent plane). The paraboloid is elliptic if every other nonempty plane section is either an ellipse, or a single point (in the case of a section by a tangent plane). A paraboloid is either elliptic or hyperbolic. Equivalently, a paraboloid may be defined as a quadric surface that is not a cylinder, and has an implicit equation whose part of degree two may be factored over the complex numbers into two different linear factors. The paraboloid is hyperbolic if the factors are real; elliptic if the factors are complex conj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
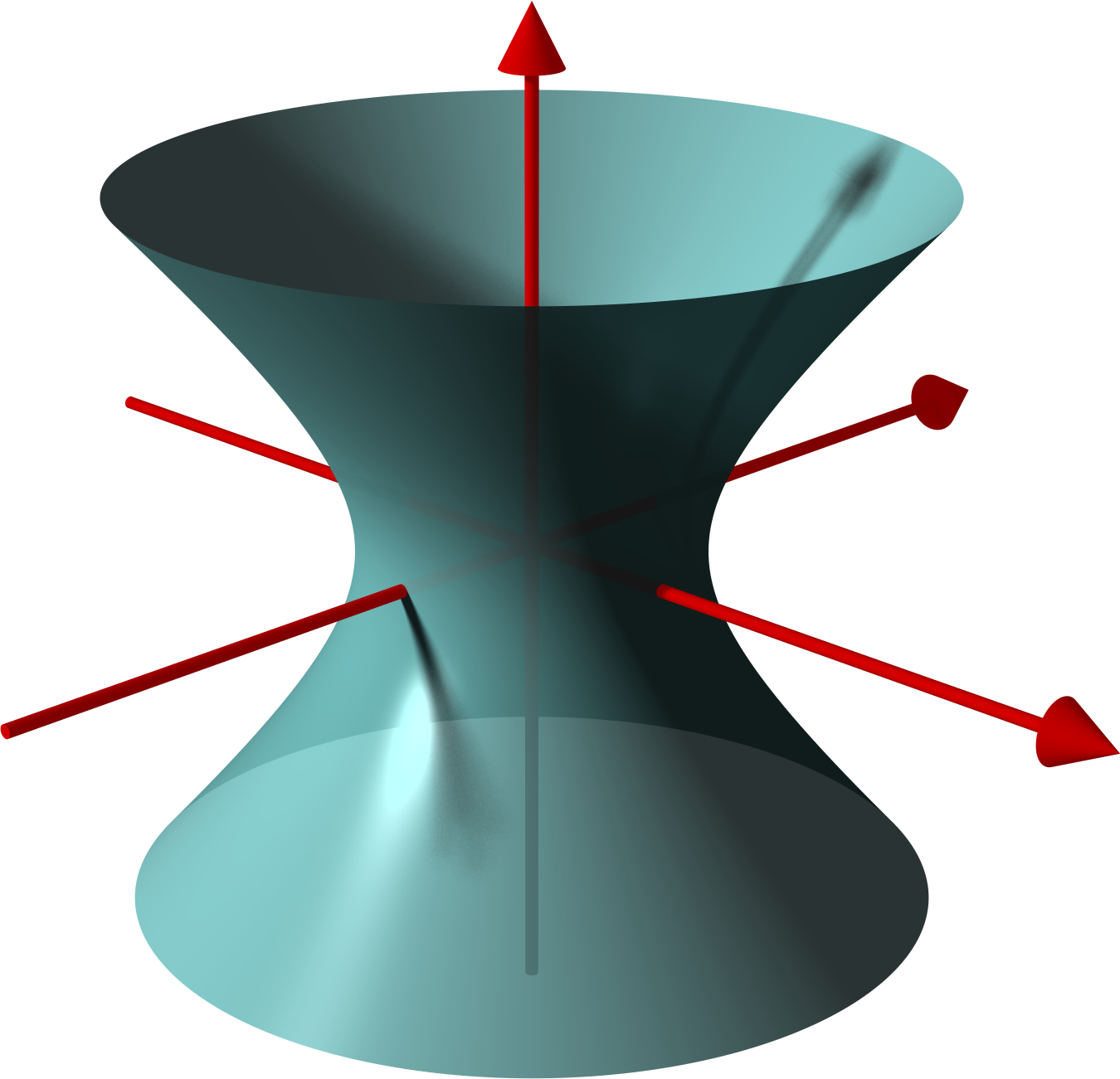
Hyperboloid Of One Sheet
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation. A hyperboloid is a quadric surface, that is, a surface defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry. Given a hyperboloid, one can choose a Cartesian coordinate system such that the hyperboloid is defined by one of the following equations: : + - = 1, or : + - = -1. The coordinate axes are axes of symmetry of the hyperboloid and the o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oloid
An oloid is a three-dimensional curved geometric object that was discovered by Paul Schatz in 1929. It is the convex hull of a skeletal frame made by placing two linked congruent circles in perpendicular planes, so that the center of each circle lies on the edge of the other circle. The distance between the circle centers equals the radius of the circles. One third of each circle's perimeter lies inside the convex hull, so the same shape may be also formed as the convex hull of the two remaining circular arcs each spanning an angle of 4π/3. Surface area and volume The surface area of an oloid is given by:. :A = 4\pi r^2 exactly the same as the surface area of a sphere with the same radius. In closed form, the enclosed volume is :V = \frac \left(2 E\left(\frac\right) + K\left(\frac\right)\right)r^, where K and E denote the complete elliptic integrals of the first and second kind respectively. A numerical calculation gives :V \approx 3.0524184684r^. Kinetics The surface o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphericon
In solid geometry, the sphericon is a solid that has a continuous developable surface with two congruent, semi-circular edges, and four vertices that define a square. It is a member of a special family of rollers that, while being rolled on a flat surface, bring all the points of their surface to contact with the surface they are rolling on. It was discovered independently by carpenter Colin Roberts (who named it) in the UK in 1969, by dancer and sculptor Alan Boeding of MOMIX in 1979, and by inventor David Hirsch, who patented it in Israel in 1980. Construction The sphericon may be constructed from a bicone (a double cone) with an apex angle of 90 degrees, by splitting the bicone along a plane through both apexes, rotating one of the two halves by 90 degrees, and reattaching the two halves. Alternatively, the surface of a sphericon can be formed by cutting and gluing a paper template in the form of four circular sectors (with central angles \pi/\sqrt) joined edge-to-e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Developable Roller
In geometry, a developable roller is a convex solid whose surface consists of a single continuous, developable face. While rolling on a plane, most developable rollers develop their entire surface so that all the points on the surface touch the rolling plane. All developable rollers have ruled surfaces. Four families of developable rollers have been described to date: the prime polysphericons, the convex hulls of the two disc rollers (TDR convex hulls), the polycons and the Platonicons. Construction Each developable roller family is based on a different construction principle. The prime polysphericons are a subfamily of the polysphericon family. They are based on bodies made by rotating regular polygons around one of their longest diagonals. These bodies are cut in two at their symmetry plane and the two halves are reunited after being rotated at an offset angle relative to each other. All prime polysphericons have two edges made of one or more circular arcs and four ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helicoid
The helicoid, also known as helical surface, after the plane and the catenoid, is the third minimal surface to be known. Description It was described by Euler in 1774 and by Jean Baptiste Meusnier in 1776. Its name derives from its similarity to the helix: for every point on the helicoid, there is a helix contained in the helicoid which passes through that point. Since it is considered that the planar range extends through negative and positive infinity, close observation shows the appearance of two parallel or mirror planes in the sense that if the slope of one plane is traced, the co-plane can be seen to be bypassed or skipped, though in actuality the co-plane is also traced from the opposite perspective. The helicoid is also a ruled surface (and a right conoid), meaning that it is a trace of a line. Alternatively, for any point on the surface, there is a line on the surface passing through it. Indeed, Catalan proved in 1842 that the helicoid and the plane were the only ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |