|
List Of Derivatives And Integrals In Alternative Calculi
There are many alternatives to the classical calculus of Newton and Leibniz; for example, each of the infinitely many non-Newtonian calculi. Occasionally an alternative calculus is more suited than the classical calculus for expressing a given scientific or mathematical idea. The table below is intended to assist people working with the alternative calculus called the "geometric calculus" (or its discrete analog). Interested readers are encouraged to improve the table by inserting citations for verification, and by inserting more functions and more calculi. Table In the following table \psi(x)=\frac is the digamma function, K(x)=e^=e^ is the K-function, (!x)=\frac is subfactorial, B_a(x)=-a\zeta(-a+1,x) are the generalized to real numbers Bernoulli polynomials. See also *Indefinite product *Product integral *Fractal derivative In applied mathematics and mathematical analysis, the fractal derivative or Hausdorff derivative is a non-Newtonian generalization of the deriva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. It has two major branches, differential calculus and integral calculus; the former concerns instantaneous Rate of change (mathematics), rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus, and they make use of the fundamental notions of convergence (mathematics), convergence of infinite sequences and Series (mathematics), infinite series to a well-defined limit (mathematics), limit. Infinitesimal calculus was developed independently in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz. Later work, including (ε, δ)-definition of limit, codify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the derivativ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-Newtonian Calculus
A non-Newtonian fluid is a fluid that does not follow Newton's law of viscosity, i.e., constant viscosity independent of stress. In non-Newtonian fluids, viscosity can change when under force to either more liquid or more solid. Ketchup, for example, becomes runnier when shaken and is thus a non-Newtonian fluid. Many salt solutions and molten polymers are non-Newtonian fluids, as are many commonly found substances such as custard, toothpaste, starch suspensions, corn starch, paint, blood, melted butter, and shampoo. Most commonly, the viscosity (the gradual deformation by shear or tensile stresses) of non-Newtonian fluids is dependent on shear rate or shear rate history. Some non-Newtonian fluids with shear-independent viscosity, however, still exhibit normal stress-differences or other non-Newtonian behavior. In a Newtonian fluid, the relation between the shear stress and the shear rate is linear, passing through the origin, the constant of proportionality being the coeffi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
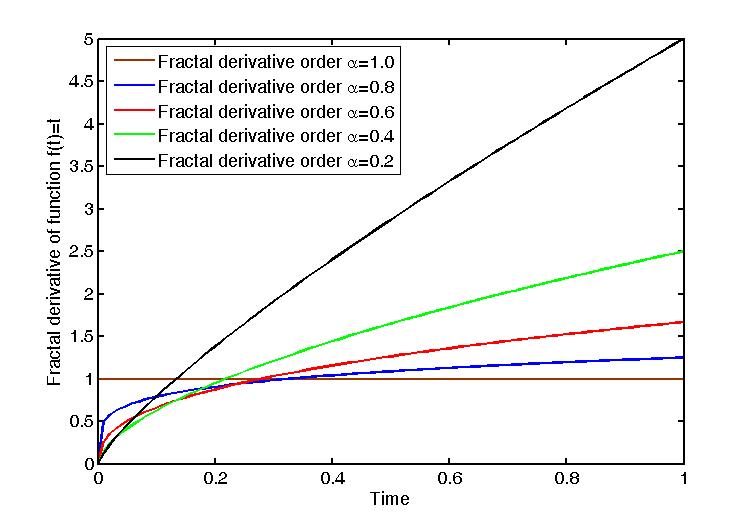
Fractal Derivative
In applied mathematics and mathematical analysis, the fractal derivative or Hausdorff derivative is a non-Newtonian generalization of the derivative dealing with the measurement of fractals, defined in fractal geometry. Fractal derivatives were created for the study of anomalous diffusion, by which traditional approaches fail to factor in the fractal nature of the media. A fractal measure ''t'' is scaled according to ''tα''. Such a derivative is local, in contrast to the similarly applied fractional derivative. Fractal calculus is formulated as a generalized of standard calculus Physical background Porous media, aquifers, turbulence, and other media usually exhibit fractal properties. Classical diffusion or dispersion laws based on random walks in free space (essentially the same result variously known as Fick's laws of diffusion, Darcy's law, and Fourier's law) are not applicable to fractal media. To address this, concepts such as distance and velocity must be redefined for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indefinite Product
In mathematics, the indefinite product operator is the inverse operator of Q(f(x)) = \frac. It is a discrete version of the geometric integral of geometric calculus, one of the non-Newtonian calculi. Some authors use term discrete multiplicative integration. Thus :Q\left( \prod_x f(x) \right) = f(x) \, . More explicitly, if \prod_x f(x) = F(x) , then :\frac = f(x) \, . If ''F''(''x'') is a solution of this functional equation for a given ''f''(''x''), then so is ''CF''(''x'') for any constant ''C''. Therefore, each indefinite product actually represents a family of functions, differing by a multiplicative constant. Period rule If T is a period of function f(x) then :\prod _x f(Tx)=C f(Tx)^ Connection to indefinite sum Indefinite product can be expressed in terms of indefinite sum: :\prod _x f(x)= \exp \left(\sum _x \ln f(x)\right) Alternative usage Some authors use the phrase "indefinite product" in a slightly different but related way to describe a product in which th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Multiplicative Derivative
Discrete may refer to: *Discrete particle or quantum in physics, for example in quantum theory * Discrete device, an electronic component with just one circuit element, either passive or active, other than an integrated circuit *Discrete group, a group with the discrete topology *Discrete category, category whose only arrows are identity arrows * Discrete mathematics, the study of structures without continuity *Discrete optimization, a branch of optimization in applied mathematics and computer science *Discrete probability distribution, a random variable that can be counted * Discrete space, a simple example of a topological space *Discrete spline interpolation, the discrete analog of ordinary spline interpolation * Discrete time, non-continuous time, which results in discrete-time samples *Discrete variable In mathematics and statistics, a quantitative variable may be continuous or discrete if they are typically obtained by ''measuring'' or '' counting'', respectively. If it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indefinite Sum
In discrete calculus the indefinite sum operator (also known as the antidifference operator), denoted by \sum _x or \Delta^ , is the linear operator, inverse of the forward difference operator \Delta . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus :\Delta \sum_x f(x) = f(x) \, . More explicitly, if \sum_x f(x) = F(x) , then :F(x+1) - F(x) = f(x) \, . If ''F''(''x'') is a solution of this functional equation for a given ''f''(''x''), then so is ''F''(''x'')+''C''(''x'') for any periodic function ''C''(''x'') with period 1. Therefore, each indefinite sum actually represents a family of functions. However, due to the Carlson's theorem, the solution equal to its Newton series expansion is unique up to an additive constant ''C''. This unique solution can be represented by formal power series form of the antidifference operator: \Delta^=\frac1. Fundamental theorem of discrete calculus Indefinite sums can be used to calculate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difference Operator
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Integral
A product integral is any Product (mathematics), product-based counterpart of the usual Summation, sum-based integral of calculus. The first product integral (''#Type I: Volterra integral, Type I'' below) was developed by the mathematician Vito Volterra in 1887 to solve systems of linear differential equations. A. Slavík''Product integration, its history and applications'' , Matfyzpress, Prague, 2007. Other examples of product integrals are the #Type II: geometric integral, geometric integral (''#Type II: geometric integral, Type II'' below), the #Type III: bigeometric integral, bigeometric integral (''#Type III: bigeometric integral, Type III'' below), and some other integrals of non-Newtonian calculus. Michael Grossman''The First Nonlinear System of Differential And Integral Calculus'' , 1979.Michael Grossman''Bigeometric Calculus: A System with a Scale-Free Derivative'' , 1983. Product integrals have found use in areas from epidemiology (the Kaplan–Meier estimator) to stochas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ..., an integral assigns numbers to functions in a way that describes Displacement (geometry), displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with Derivative, differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a "natural philosopher"), widely recognised as one of the greatest mathematicians and physicists and among the most influential scientists of all time. He was a key figure in the philosophical revolution known as the Enlightenment. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for developing infinitesimal calculus. In the , Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. Newton used his mathematical description of gravity to derive Kepler's laws of planetary motion, account for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |