|
Linear Filter
Linear filters process time-varying input signals to produce output signals, subject to the constraint of linearity. In most cases these linear filters are also time invariant (or shift invariant) in which case they can be analyzed exactly using LTI ("linear time-invariant") system theory revealing their transfer functions in the frequency domain and their impulse responses in the time domain. Real-time implementations of such linear signal processing filters in the time domain are inevitably causal, an additional constraint on their transfer functions. An analog electronic circuit consisting only of linear components (resistors, capacitors, inductors, and linear amplifiers) will necessarily fall in this category, as will comparable mechanical systems or digital signal processing systems containing only linear elements. Since linear time-invariant filters can be completely characterized by their response to sinusoids of different frequencies (their frequency response), they are so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearity
Linearity is the property of a mathematical relationship (''function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear relationship of voltage and current in an electrical conductor (Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships are ''nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. The word linear comes from Latin ''linearis'', "pertaining to or resembling a line". In mathematics In mathematics, a linear map or linear function ''f''(''x'') is a function that satisfies the two properties: * Additivity: . * Homogeneity of degree 1: for all α. These properties are known as the superposition principle. In this definition, ''x'' is not necessarily a real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal (information Theory)
In signal processing, a signal is a function that conveys information about a phenomenon. Any quantity that can vary over space or time can be used as a signal to share messages between observers. The ''IEEE Transactions on Signal Processing'' includes audio, video, speech, image, sonar, and radar as examples of signal. A signal may also be defined as observable change in a quantity over space or time (a time series), even if it does not carry information. In nature, signals can be actions done by an organism to alert other organisms, ranging from the release of plant chemicals to warn nearby plants of a predator, to sounds or motions made by animals to alert other animals of food. Signaling occurs in all organisms even at cellular levels, with cell signaling. Signaling theory, in evolutionary biology, proposes that a substantial driver for evolution is the ability of animals to communicate with each other by developing ways of signaling. In human engineering, signals are typi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amplifier
An amplifier, electronic amplifier or (informally) amp is an electronic device that can increase the magnitude of a signal (a time-varying voltage or current). It may increase the power significantly, or its main effect may be to boost the voltage or current (power, voltage or current amplifier). It is a two-port electronic circuit that uses electric power from a power supply to increase the amplitude of a signal applied to its input terminals, producing a greater amplitude signal at its output. The ratio of output to input voltage, current, or power is termed gain (voltage, current, or power gain). An amplifier, by definition has gain greater than unity (if the gain is less than unity, the device is an attenuator). An amplifier can either be a separate piece of equipment or an electrical circuit contained within another device. Amplification is fundamental to modern electronics, and amplifiers are widely used in almost all electronic equipment. Amplifiers can be categorize ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resistor
A resistor is a passive two-terminal electrical component that implements electrical resistance as a circuit element. In electronic circuits, resistors are used to reduce current flow, adjust signal levels, to divide voltages, bias active elements, and terminate transmission lines, among other uses. High-power resistors that can dissipate many watts of electrical power as heat may be used as part of motor controls, in power distribution systems, or as test loads for generators. Fixed resistors have resistances that only change slightly with temperature, time or operating voltage. Variable resistors can be used to adjust circuit elements (such as a volume control or a lamp dimmer), or as sensing devices for heat, light, humidity, force, or chemical activity. Resistors are common elements of electrical networks and electronic circuits and are ubiquitous in electronic equipment. Practical resistors as discrete components can be composed of various compounds and forms. Resisto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inductor
An inductor, also called a coil, choke, or reactor, is a passive two-terminal electrical component that stores energy in a magnetic field when electric current flows through it. An inductor typically consists of an insulated wire wound into a coil. When the current flowing through the coil changes, the time-varying magnetic field induces an electromotive force (''emf'') (voltage) in the conductor, described by Faraday's law of induction. According to Lenz's law, the induced voltage has a polarity (direction) which opposes the change in current that created it. As a result, inductors oppose any changes in current through them. An inductor is characterized by its inductance, which is the ratio of the voltage to the rate of change of current. In the International System of Units (SI), the unit of inductance is the henry (H) named for 19th century American scientist Joseph Henry. In the measurement of magnetic circuits, it is equivalent to . Inductors have values that typically ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capacitor
A capacitor is a device that stores electrical energy in an electric field by virtue of accumulating electric charges on two close surfaces insulated from each other. It is a passive electronic component with two terminals. The effect of a capacitor is known as capacitance. While some capacitance exists between any two electrical conductors in proximity in a circuit, a capacitor is a component designed to add capacitance to a circuit. The capacitor was originally known as the condenser, a term still encountered in a few compound names, such as the ''condenser microphone''. The physical form and construction of practical capacitors vary widely and many types of capacitor are in common use. Most capacitors contain at least two electrical conductors often in the form of metallic plates or surfaces separated by a dielectric medium. A conductor may be a foil, thin film, sintered bead of metal, or an electrolyte. The nonconducting dielectric acts to increase the capacitor's c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
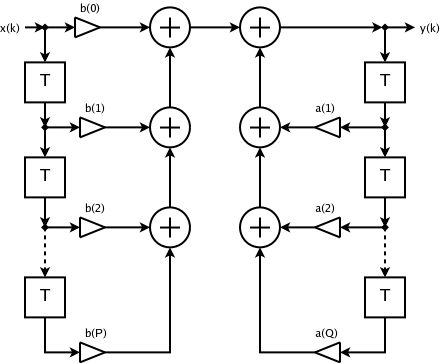
Finite Impulse Response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely (usually decaying). The impulse response (that is, the output in response to a Kronecker delta input) of an Nth-order discrete-time FIR filter lasts exactly N+1 samples (from first nonzero element through last nonzero element) before it then settles to zero. FIR filters can be discrete-time or continuous-time, and digital or analog. Definition For a causal discrete-time FIR filter of order ''N'', each value of the output sequence is a weighted sum of the most recent input values: :\begin y &= b_0 x + b_1 x -1+ \cdots + b_N x -N\\ &= \sum_^N b_i\cdot x -i \end where: * x /math> is the input signal, * y /math> is the output signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Impulse Response
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response h(t) which does not become exactly zero past a certain point, but continues indefinitely. This is in contrast to a finite impulse response (FIR) system in which the impulse response ''does'' become exactly zero at times t>T for some finite T, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as ''IIR systems'' or ''IIR filters''. In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Of A Polynomial
In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial's monomials (individual terms) with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. For a univariate polynomial, the degree of the polynomial is simply the highest exponent occurring in the polynomial. The term order has been used as a synonym of ''degree'' but, nowadays, may refer to several other concepts (see order of a polynomial (other)). For example, the polynomial 7x^2y^3 + 4x - 9, which can also be written as 7x^2y^3 + 4x^1y^0 - 9x^0y^0, has three terms. The first term has a degree of 5 (the sum of the powers 2 and 3), the second term has a degree of 1, and the last term has a degree of 0. Therefore, the polynomial has a degree of 5, which is the highest degree of any term. To determine the degree of a polynomial that is not in standard form, such as (x+1)^2 - (x-1)^2, one can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling Period
In signal processing, sampling is the reduction of a continuous-time signal to a discrete-time signal. A common example is the conversion of a sound wave to a sequence of "samples". A sample is a value of the signal at a point in time and/or space; this definition differs from the usage in statistics, which refers to a set of such values. A sampler is a subsystem or operation that extracts samples from a continuous signal. A theoretical ideal sampler produces samples equivalent to the instantaneous value of the continuous signal at the desired points. The original signal can be reconstructed from a sequence of samples, up to the Nyquist limit, by passing the sequence of samples through a type of low-pass filter called a reconstruction filter. Theory Functions of space, time, or any other dimension can be sampled, and similarly in two or more dimensions. For functions that vary with time, let ''S''(''t'') be a continuous function (or "signal") to be sampled, and let sam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolved
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). The integral is evaluated for all values of shift, producing the convolution function. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution (f*g) differs from cross-correlation (f \star g) only in that either or is reflected about the y-axis in convolution; thus it is a cross-c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superposition Principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input ''A'' produces response ''X'' and input ''B'' produces response ''Y'' then input (''A'' + ''B'') produces response (''X'' + ''Y''). A function F(x) that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity F(x_1+x_2)=F(x_1)+F(x_2) \, and homogeneity F(a x)=a F(x) \, for scalar . This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathematically; the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.jpg)