|
Level Set Method
Level or levels may refer to: Engineering *Level (optical instrument), a device used to measure true horizontal or relative heights *Spirit level or bubble level, an instrument designed to indicate whether a surface is horizontal or vertical *Canal pound or level *Regrading or levelling, the process of raising and/or lowering the levels of land *Storey or level, a vertical unit of a building or a mine *Level (coordinate), vertical position *Horizontal plane parallel Gaming *Level (video games), a stage of the game *Level (role-playing games), a measurement of character development Music *Level (music), similar to but more general and basic than a chord * "Level" (The Raconteurs song) * ''Levels'' (album), an album by AKA * "Levels" (Avicii song) * "Levels" (Bilal song) * "Levels" (Nick Jonas song) * "Levels" (Meek Mill song) * "Levels" (NorthSideBenji song), featuring Houdini * "Levels" (Sidhu Moose Wala song) Places * Level Mountain, a volcano in northern British Columbia, Can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Level (optical Instrument)
A level is an optical instrument used to establish or verify points in the same horizontal plane in a process known as ''levelling''. It is used in conjunction with a levelling staff to establish the relative height or levels (the vertical separation) of objects or marks. It is widely used in surveying and construction to measure height differences and to transfer, measure, and set heights of known objects or marks. It is also known as a surveyor's level, builder's level, dumpy level or the historic "Y" level. It operates on the principle of establishing a visual level relationship between two or more points, for which an inbuilt optical telescope and a highly accurate bubble level are used to achieve the necessary accuracy. Traditionally the instrument was completely adjusted manually to ensure a level line of sight, but modern automatic versions self-compensate for slight errors in the coarse levelling of the instrument, and are thereby quicker to use. The optical level should ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Levels (Sidhu Moose Wala Song)
"Levels" is a song by Indian rapper-singer Sidhu Moose Wala featuring Canadian rapper Sunny Malton. The song was written by him and was released four days before his assassination on 29 May 2022 in a village named Jawarkhe near his village Moosa. Lyrical content In the song, Sidhu speaks about his personal feuds with singers who he made famous such as Prem Dhillon Premjeet Singh Dhillon (born 4 January 1995) is an Indian singer and songwriter associated with Music of Punjab, Punjabi music. Dhillon is best known for singles "Boot Cut", "Old Skool" and "Majha Block". Personal life Premjeet Singh Dhillon w ..., Nseeb and his old rivals like Karan Aujla and Babbu Maan. Commercial performance It received over 200,000,000 views on Youtube. Credits and personnel * Sidhu Moose Wala, Sunny Malton – songwriting *The Kidd – production *Nav Dhimman – mixing and engineering *Vishal Chaudhary – artwork Charts Certifications References {{Auth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Categorical Variable
In statistics, a categorical variable (also called qualitative variable) is a variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a particular group or nominal category on the basis of some qualitative property. In computer science and some branches of mathematics, categorical variables are referred to as enumerations or enumerated types. Commonly (though not in this article), each of the possible values of a categorical variable is referred to as a level. The probability distribution associated with a random categorical variable is called a categorical distribution. Categorical data is the statistical data type consisting of categorical variables or of data that has been converted into that form, for example as grouped data. More specifically, categorical data may derive from observations made of qualitative data that are summarised as counts or cross tabulations, or from observat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Level (logarithmic Quantity)
In science and engineering, a power level and a field level (also called a root-power level) are logarithmic magnitudes of certain quantities referenced to a standard reference value of the same type. * A ''power level'' is a logarithmic quantity used to measure power, power density or sometimes energy, with commonly used unit decibel (dB). * A ''field level'' (or ''root-power level'') is a logarithmic quantity used to measure quantities of which the square is typically proportional to power (for instance, the square of voltage is proportional to power by the inverse of the conductor's resistance), etc., with commonly used units neper (Np) or decibel (dB). The type of level and choice of units indicate the scaling of the logarithm of the ratio between the quantity and its reference value, though a logarithm may be considered to be a dimensionless quantity. The reference values for each type of quantity are often specified by international standards. Power and field levels are use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Level (algebra)
In field theory (mathematics), field theory, a branch of mathematics, the Stufe (/Help:IPA for German, ʃtuːfə/; German: level) ''s''(''F'') of a field (mathematics), field ''F'' is the least number of squares that sum to −1. If −1 cannot be written as a sum of squares, ''s''(''F'') = \infty. In this case, ''F'' is a formally real field. Albrecht Pfister (mathematician), Albrecht Pfister proved that the Stufe, if finite, is always a power of 2, and that conversely every power of 2 occurs. Powers of 2 If s(F)\ne\infty then s(F)=2^k for some natural number k.Rajwade (1993) p.13Lam (2005) p.379 ''Proof:'' Let k \in \mathbb N be chosen such that 2^k \leq s(F) < 2^. Let . Then there are elements such that : Both and are sums of squares, and , since otherwise |
Quantity
Quantity or amount is a property that can exist as a multitude or magnitude, which illustrate discontinuity and continuity. Quantities can be compared in terms of "more", "less", or "equal", or by assigning a numerical value multiple of a unit of measurement. Mass, time, distance, heat, and angle are among the familiar examples of quantitative properties. Quantity is among the basic classes of things along with quality, substance, change, and relation. Some quantities are such by their inner nature (as number), while others function as states (properties, dimensions, attributes) of things such as heavy and light, long and short, broad and narrow, small and great, or much and little. Under the name of multitude comes what is discontinuous and discrete and divisible ultimately into indivisibles, such as: ''army, fleet, flock, government, company, party, people, mess (military), chorus, crowd'', and ''number''; all which are cases of collective nouns. Under the name of magni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Great Level
Great may refer to: Descriptions or measurements * Great, a relative measurement in physical space, see Size * Greatness, being divine, majestic, superior, majestic, or transcendent People * List of people known as "the Great" * Artel Great (born 1981), American actor * Great Osobor (born 2002), Spanish-born British basketball player Other uses * ''Great'' (1975 film), a British animated short about Isambard Kingdom Brunel * ''Great'' (2013 film), a German short film * Great (supermarket), a supermarket in Hong Kong * GReAT, Graph Rewriting and Transformation, a Model Transformation Language * Gang Resistance Education and Training Gang Resistance Education And Training, abbreviated G.R.E.A.T., provides a school-based, police officer-instructed program in America that includes classroom instruction and a variety of learning activities. The program was originally adminis ..., or GREAT, a school-based and police officer-instructed program * Global Research and Analysis Te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Somerset Levels
The Somerset Levels are a coastal plain and wetland area of Somerset, England, running south from the Mendips to the Blackdown Hills. The Somerset Levels have an area of about and are bisected by the Polden Hills; the areas to the south are drained by the River Parrett, and the areas to the north by the rivers Axe and Brue. The Mendip Hills separate the Somerset Levels from the North Somerset Levels. The Somerset Levels consist of marine clay "levels" along the coast and inland peat-based "moors"; agriculturally, about 70 per cent is used as grassland and the rest is arable. Willow and teazel are grown commercially and peat is extracted. A Palaeolithic flint tool found in West Sedgemoor is the earliest indication of human presence in the area. The Neolithic people exploited the reed swamps for their natural resources and started to construct wooden trackways, including the world's oldest known timber trackway, the Post Track, dating from about 3800 BC. The Le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Levels, West Virginia
Levels is an Unincorporated area, unincorporated community in Hampshire County, West Virginia, Hampshire County in the U.S. state of West Virginia. According to the United States Census, 2000, 2000 census, the Levels community has a population of 147. It is home to John J. Cornwell Elementary School. The community was so named on account of the relatively level original town site. Levels was originally known as Levels Cross Roads because of its location at the intersection of four roads in north-central Hampshire County: Bright's Hollow Road (county road, County Route 5/5) north to Okonoko, West Virginia, Okonoko, Little Cacapon-Levels Road (County Route 3/3) southeast to Slanesville, West Virginia, Slanesville, Jersey Mountain Road (County Route 5) south to Romney, West Virginia, Romney, and Frenches Station Road (County Route 5/7) northwest to South Branch Depot, West Virginia, South Branch Depot. Notable residents *Howard Llewellyn Swisher (1870–1945), American businessper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
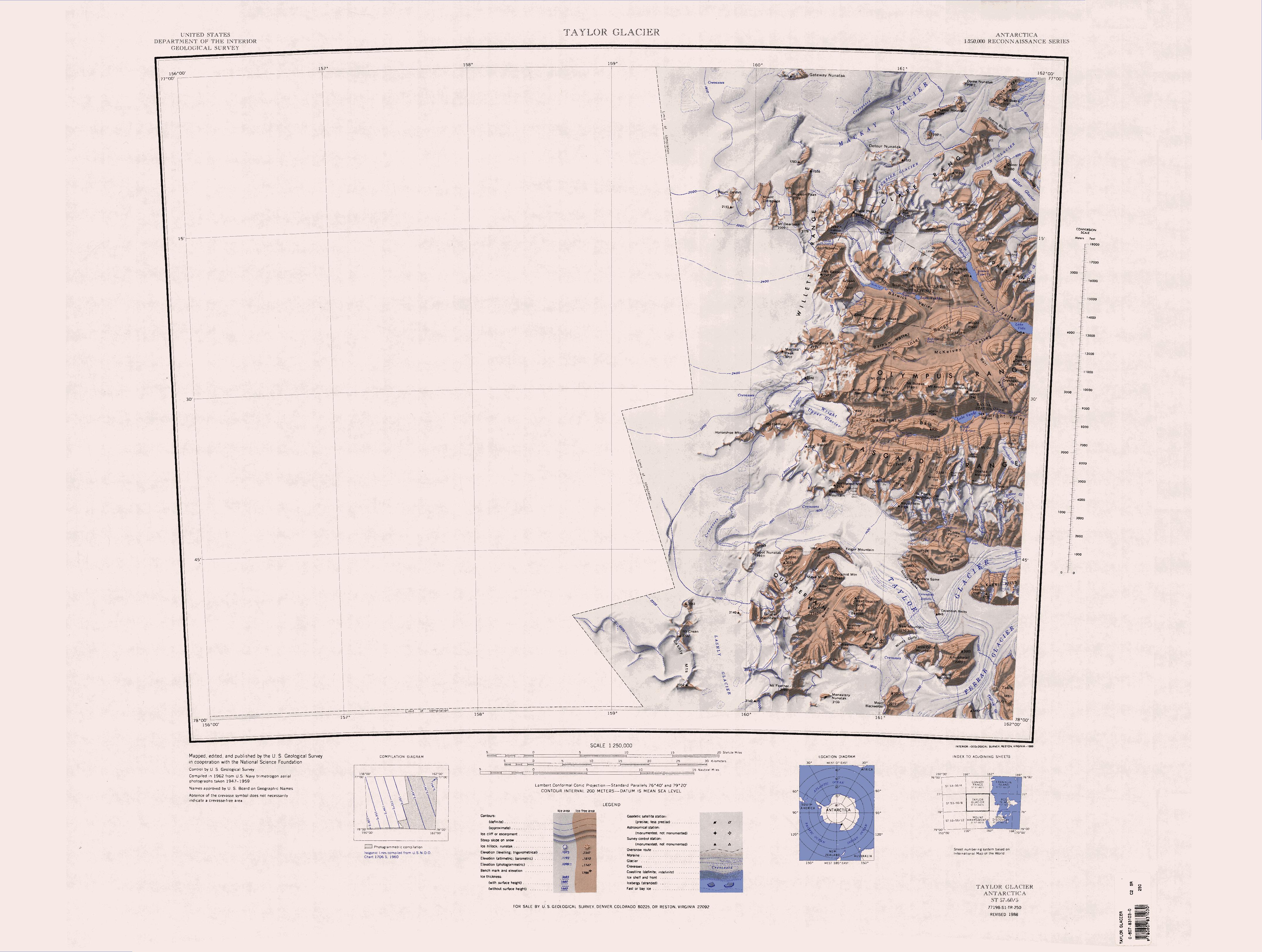
Level Valley
The Wilkniss Mountains () form a prominent group of conical peaks and mountains, long running north–south, located east-southeast of Mount Feather in the Quartermain Mountains, Victoria Land, Antarctica. The mountains are wide in the north portion where Mount Blackwelder, high, and Pivot Peak high, rise above ice-free valleys. Except for an outlying southwest peak, the south portion narrows to a series of mainly ice-covered smaller peaks. Name The Wilkniss Mountains were named by United States Advisory Committee on Antarctic Names (US-ACAN) in 1992 after Peter E. Wilkniss, a chemist who from 1975 has served in various positions at the National Science Foundation, including Deputy Assistant Director of the Directorate for Scientific, Technological, and International Affairs; Director, Division of Polar Programs, 1984–93; senior science associate to the assistant director for Geosciences, from 1993. Location The Wilkniss Mountains are south of the Knobhead massif, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
The Level, Brighton
The Level is an urban park in central Brighton, on the south coast of England. The park is a triangle of bounded by Union Road to the north, Richmond Terrace (A270) to the east, and Ditchling Road ( A23) to the west. In the past, the land has been used as a cricket ground for the Prince of Wales and as a setting for large-scale dinner parties to commemorate events such as the defeat of Napoleon Bonaparte and the coronation of Queen Victoria. The Level is often used for public meetings and gatherings. These have included May Day events, a 1983 peace camp and the Brighton Urban Free Festival. Present day features of the park include a grassed area with elm trees and outdoor seating, a skatepark, public toilets, a rose garden, a children's playground and a water feature. The park was substantially redeveloped from 2009 onwards. Overview The Level is in central Brighton, about north of the seafront. It now covers but was originally much bigger, encompassing the present-d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Level, Ohio
Level is an unincorporated community in southern Harlan Township, Warren County, Ohio, United States, which in the 19th century was a station on the Marietta and Cincinnati Railroad and had its own post office, since closed. According to the U.S. Geographic Names Information System (GNIS), an alternate name for this community is ''Windsor''. Level was not officially plat In the United States, a plat ( or ) (plan) is a cadastral map, drawn to scale, showing the divisions of a piece of land. United States General Land Office surveyors drafted township plats of Public Lands Survey System, Public Lands Surveys to ...ted. A post office called Level was established in 1834, and remained in operation until 1905. References Unincorporated communities in Warren County, Ohio Unincorporated communities in Ohio {{WarrenCountyOH-geo-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |